在4*4*4的3维空间内取3个点有64*63*62/6=41664种取法,但在xy,xz,yz面可自由变换的条件下只有29个不同的结构。

| 结构 | 数量 |
| 1 | 64 |
| 8 | 64 |
| 20 | 64 |
第一种情况3个点共两面,图中结构就是1,1绕着z轴旋转得到8,绕y轴旋转得到20.在4*4*4的范围内这样的结构有64个。

| 结构 | 数量 |
| 14 | 384 |
| 24 | 384 |
| 27 | 384 |
第二种情况,3个点共一面。图中为14,14绕y轴得到27,绕x轴得到24

| 结构 | 数量 |
| 29 | 2304 |
3个但不共面,就是体对角线

| 结构 | 数量 |
| 17 | 3456 |
| 18 | 3456 |
| 25 | 3456 |
2个点共1个面,第3点与此2点都不共面,图中是17,17绕z轴得到18,绕y轴得到25
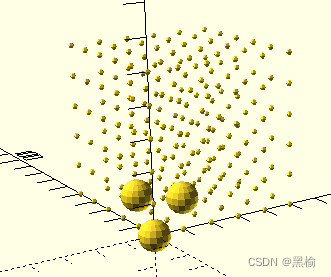
| 结构 | 数量 |
| 16 | 1728 |
16,图中3个点,任意两点都共面,这种结构只有1个
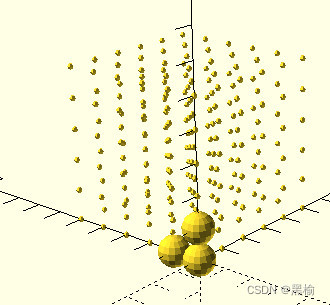
| 结构 | 数量 |
| 2 | 576 |
| 4 | 576 |
| 10 | 576 |
3个点共一面,其中有1个点与另外2个点各共另两面,图中是2,2绕y轴得到10.绕x轴得到4

| 结构 | 数量 |
| 6 | 1728 |
| 11 | 1728 |
| 15 | 1728 |
有两点共2面,有两点共1面,有两点不共面。图中为6.这个结构绕z轴得到11,6绕y轴得到15,每个结构有1728个。
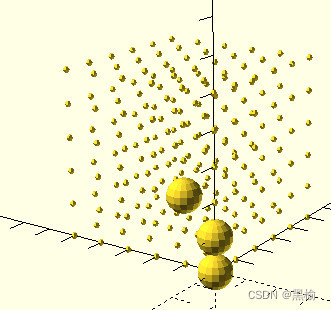
| 结构 | 数量 |
| 3 | 576 |
| 9 | 576 |
| 22 | 576 |
3点共1面,其中有两点共2面,另外两两间只共1面。图中为3.3绕z轴得到9.3绕y轴得到22.
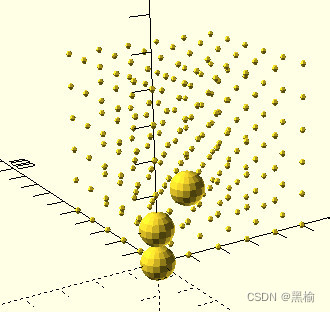
| 结构 | 数量 |
| 5 | 576 |
| 12 | 576 |
| 21 | 576 |
图中结构为5,把5绕z轴得到12,5绕y轴得到21.
5绕x轴得到3,12绕x轴得到22,21绕x轴得到9.
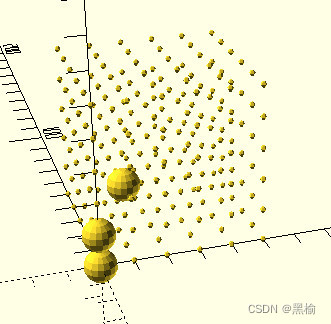
| 结构 | 数量 |
| 7 | 1728 |
| 13 | 1728 |
| 23 | 1728 |
有两点共2面,第3点和这两点都不共面,图中若为7,7绕z轴得13.绕y轴得到23.

| 结构 | 数量 |
| 19 | 3456 |
| 26 | 3456 |
| 28 | 3456 |
最后一种情况,有两点共一面,另外一点与这两点不共面。图中为19,19绕y轴得到28,绕x轴得到26.
各种分布占比
| 结构 | 数量 | 占比 | |
| 1 | 19 | 3456 | 0.083 |
| 2 | 17 | 3456 | 0.083 |
| 3 | 7 | 1728 | 0.041 |
| 4 | 6 | 1728 | 0.041 |
| 5 | 3+5 | 1152 | 0.028 |
| 6 | 29 | 768 | 0.018 |
| 7 | 2 | 576 | 0.014 |
| 8 | 16 | 576 | 0.014 |
| 9 | 14 | 384 | 0.009 |
| 10 | 1 | 64 | 0.002 |
因为结构3和5两组可以通过旋转得到,因此视为1组。所以共有10组。结构19占比最多,结构1占比最少。
所以如果有3个粒子被束缚在4*4*4的范围内自由的运动,任一时间观察这3个粒子,他们按结构19分布的概率最大。现在假设观察的结果是结构19的占比少了1%,而结构17的占比多了1%,可以认为是外力改变了粒子的运动,或者是空间的外形发生了变化/。所以这里力和空间的形状可以实现同样的效果。
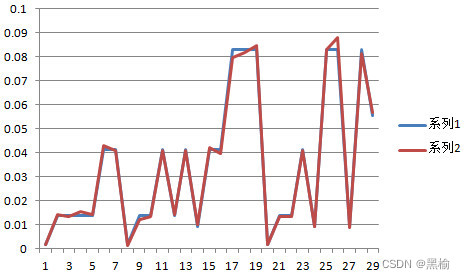
| 结构 | 数量 | 随机 | ||
| 1 | 64 | 0.00154 | 16 | 0.0016 |
| 2 | 576 | 0.01382 | 142 | 0.0142 |
| 3 | 576 | 0.01382 | 134 | 0.0134 |
| 4 | 576 | 0.01382 | 156 | 0.0156 |
| 5 | 576 | 0.01382 | 141 | 0.0141 |
| 6 | 1728 | 0.04147 | 430 | 0.043 |
| 7 | 1728 | 0.04147 | 410 | 0.041 |
| 8 | 64 | 0.00154 | 14 | 0.0014 |
| 9 | 576 | 0.01382 | 121 | 0.0121 |
| 10 | 576 | 0.01382 | 134 | 0.0134 |
| 11 | 1728 | 0.04147 | 409 | 0.0409 |
| 12 | 576 | 0.01382 | 141 | 0.0141 |
| 13 | 1728 | 0.04147 | 410 | 0.041 |
| 14 | 384 | 0.00922 | 99 | 0.0099 |
| 15 | 1728 | 0.04147 | 421 | 0.0421 |
| 16 | 1728 | 0.04147 | 398 | 0.0398 |
| 17 | 3456 | 0.08295 | 795 | 0.0795 |
| 18 | 3456 | 0.08295 | 817 | 0.0817 |
| 19 | 3456 | 0.08295 | 847 | 0.0847 |
| 20 | 64 | 0.00154 | 16 | 0.0016 |
| 21 | 576 | 0.01382 | 135 | 0.0135 |
| 22 | 576 | 0.01382 | 134 | 0.0134 |
| 23 | 1728 | 0.04147 | 410 | 0.041 |
| 24 | 384 | 0.00922 | 91 | 0.0091 |
| 25 | 3456 | 0.08295 | 832 | 0.0832 |
| 26 | 3456 | 0.08295 | 882 | 0.0882 |
| 27 | 384 | 0.00922 | 87 | 0.0087 |
| 28 | 3456 | 0.08295 | 812 | 0.0812 |
| 29 | 2304 | 0.0553 | 566 | 0.0566 |
随机1万次,验算数据