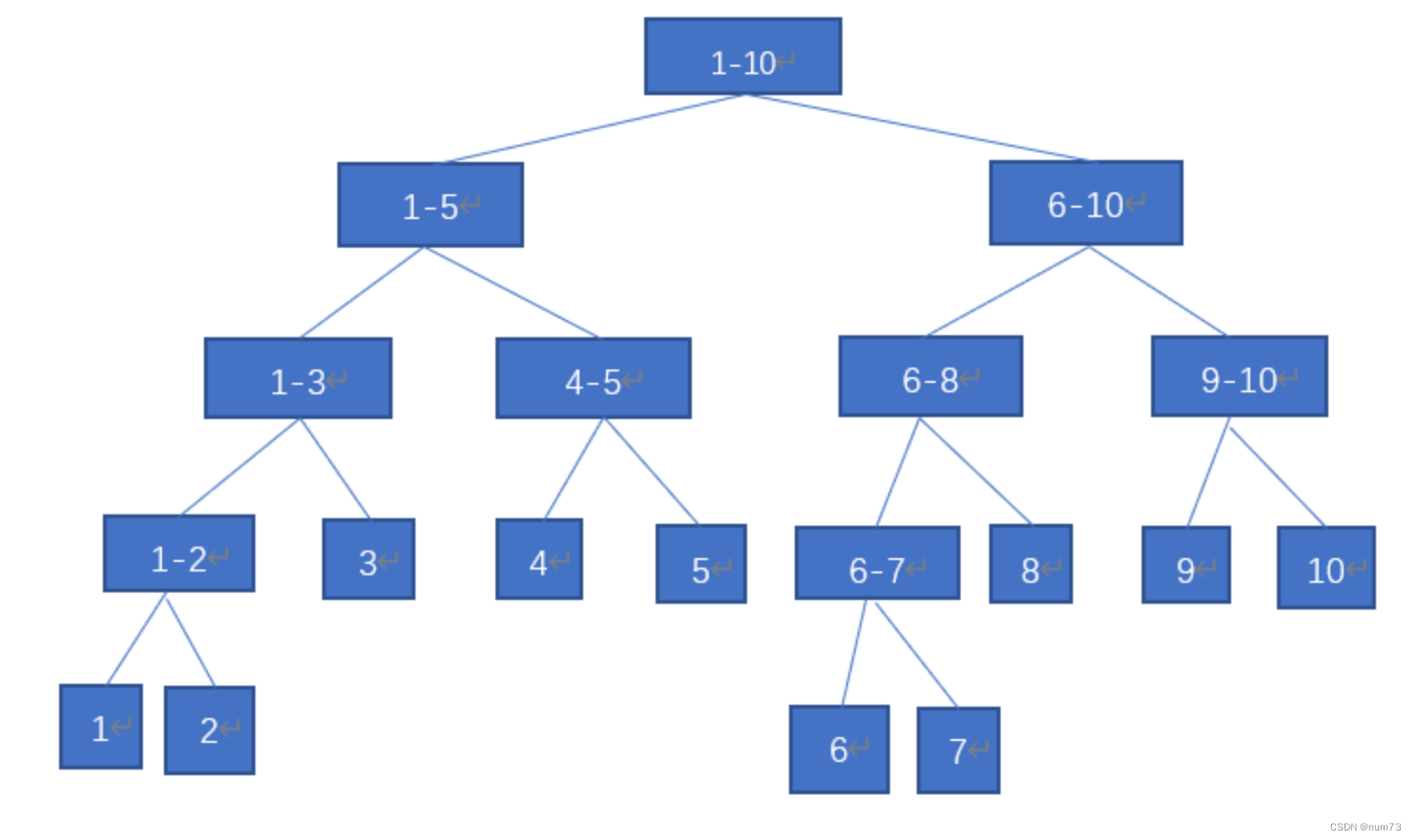
背景描述
本数据集的工资数据截至 2023-24 赛季夏季转会窗口。数据提取自游戏《Football Manager 2024》,包含 40,000+ 名球员的数据。
FM24 是一款深受欢迎的足球模拟经营游戏。玩家将扮演一位足球经理,负责经营一支足球俱乐部,通过合理的人员调整、战术布置和训练安排,带领球队取得胜利。
数据说明
data_raw.csv
| 字段 | 说明 |
|---|---|
| Name | 球员名字 |
| Club | 俱乐部 |
| Division | 联赛 |
| Based | 联赛举办国 |
| Nat | 国籍 |
| EU National | 是否为欧洲国家 |
| Caps | 出场次数 |
| AT Apps | 所有出场时间 |
| Position | 位置 |
| Age | 年龄 |
| CR | 影响力(0-10000) |
| Begins | 合同开始日期 |
| Expires | 合同截止日期 |
| Last Club | 上一家俱乐部 |
| Last Trans. Fee | 转会费 |
| Salary | 工资 |
data_cleaned.csv
| 字段 | 说明 |
|---|---|
| Is_top_5_League | 是否在在五大联赛效力 |
| Based_rich_nation | 球员生活的国家是否富裕 |
| Is_top_ranked_nation | 球员所代表的国家是否在国际足联世界排名中名列前茅 |
| EU_National | 是否为欧洲国家 |
| Caps | 出场次数 |
| Apps | 所有出场时间 |
| Age | 年龄 |
| Reputation | 影响力(0-10000) |
| Is_top_prev_club | 根据欧足联 10 年系数,前俱乐部球员是否曾在顶级俱乐部效力过 |
| Last_Transfer_Fee | 转会费 |
| Salary | 工资 |
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import plotly.express as px
import seaborn as sns
from scipy import stats
from scipy.stats import kstest,ttest_ind,spearmanr,f_oneway
from sklearn.preprocessing import StandardScaler
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.stats.stattools import durbin_watson
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
from statsmodels.stats.diagnostic import het_breuschpagan
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
from sklearn.linear_model import LinearRegression
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = ['Microsoft YaHei']首先我们先导入用到的库,其次设置绘图时的字体为微软雅黑,防止绘图时中文出现乱码情况
df1 = pd.read_csv('D:/每周挑战/data_raw.csv')
df2 = pd.read_csv('D:/每周挑战/data_cleaned.csv')
# print(df1.info())
# print('//')
# print(df2.info())从数据上来看df1属于未处理的数据,而df2属于清洗后的数据,因此我们分析时,只需分析清洗后的数据即可
# 虽然数据里的特征全是数值型的,但是由于含义不同,我们可以将其分为连续的和不连续的
feature1 = ['Is_top_5_League','Based_rich_nation','Is_top_ranked_nation','EU_National','Is_top_prev_club']
# for f in feature1:
# data = df2[f].value_counts().reset_index()
# plt.figure(figsize=(10,8))
# sns.barplot(data,x='index',y=f)# plt.show() # 如果你的运行环境是pycharm,如果环境是jupyter notebook不建议这样写,因为这样可能导致图像无法一起显示fig,axes = plt.subplots(3,2,figsize=(16,15))
for i,f in enumerate(feature1):data = df2[f].value_counts().reset_index()fig = sns.barplot(data,x='index',y=f,ax=axes[i//2,i%2])fig.set_title(f)
feature2 = ['Caps','Apps','Age','Reputation','Last_Transfer_Fee','Salary']fig,axes = plt.subplots(3,2,figsize=(16,15))
for i,f in enumerate(feature2):data = df2[f]sns.histplot(data,ax = axes[i//2,i%2],kde=True)
# fig.set_title(f) 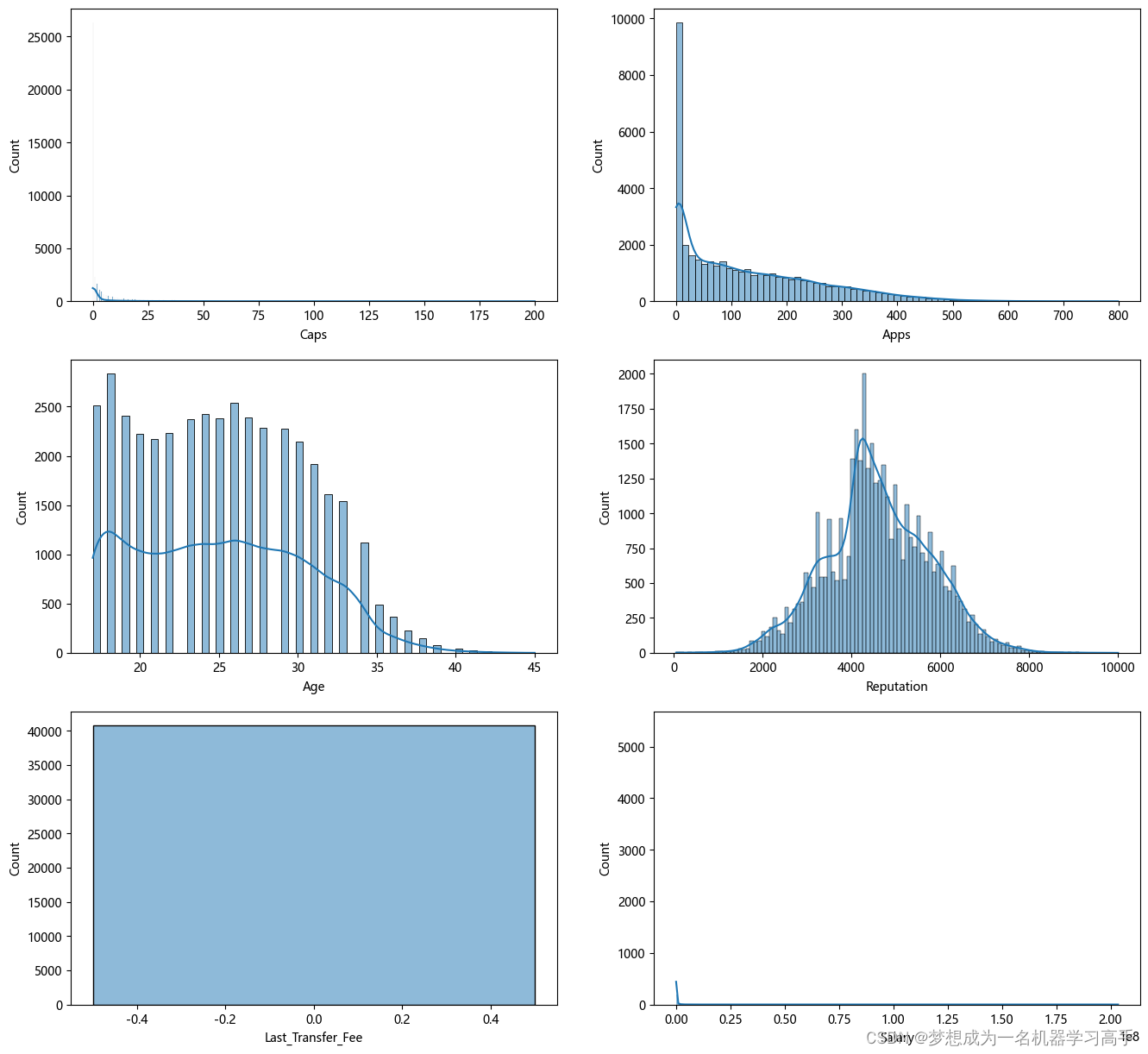
plt.figure(figsize=(10,8))
a = df2['Last_Transfer_Fee'].reset_index()
sns.scatterplot(a,x='index',y='Last_Transfer_Fee')
plt.title('转会费分布情况')
plt.show()
plt.figure(figsize=(10,8))
b = df2['Salary'].reset_index()
sns.scatterplot(b,x='index',y='Salary')
plt.title('薪资分布情况')
plt.show() 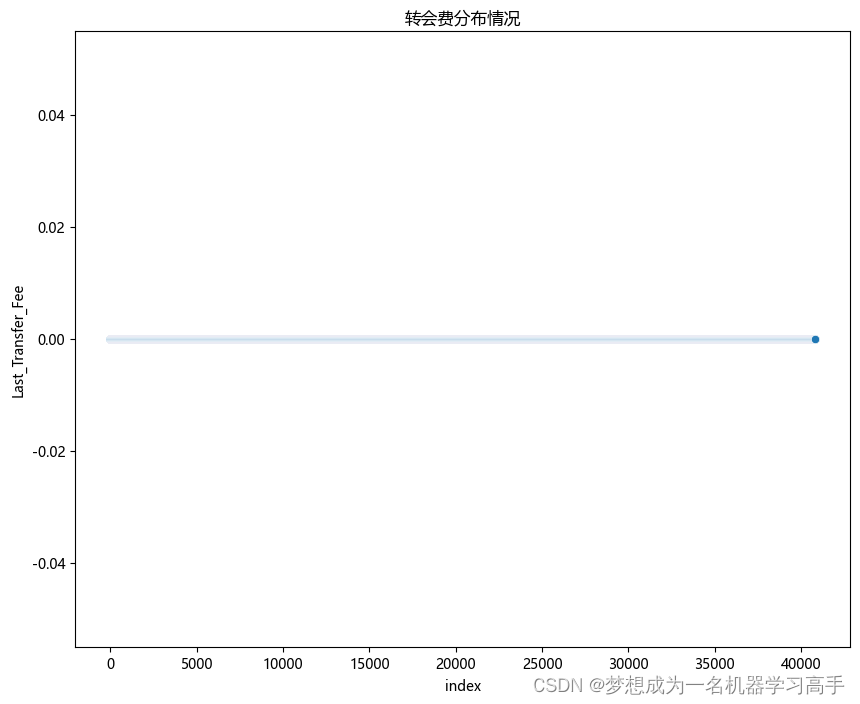
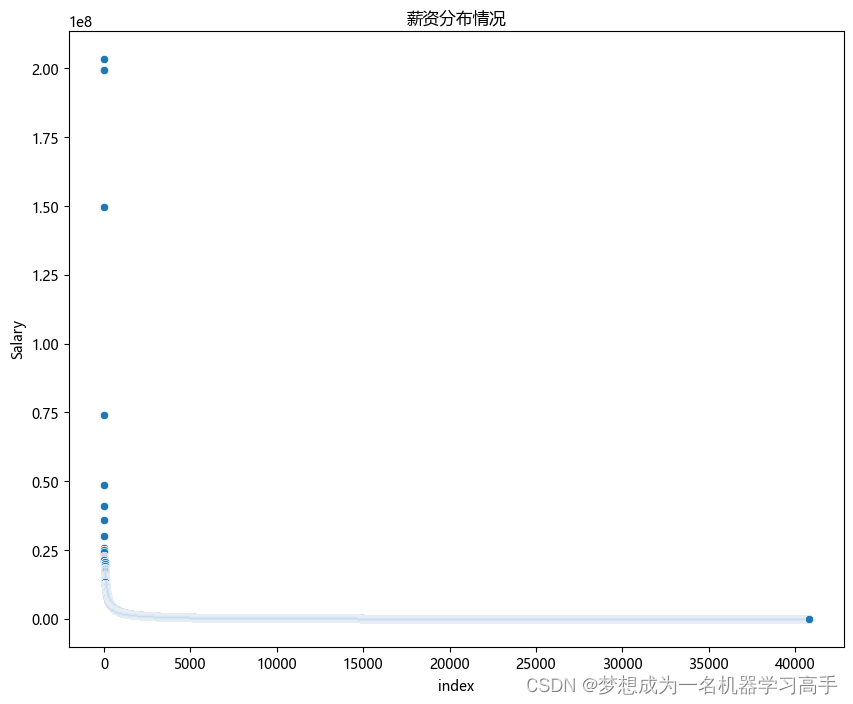
接下来,我们可以对各个特征之间的相关性来进行判断 对于相关性的判断我们可以使用热力图,皮尔逊相关系数,斯皮尔曼相关系数等, 使用皮尔逊相关系数有一个硬性条件就是数据的分布特征必须符合正态分布,因此我们先对连续型数值数据进行KS检验
feature3 = ['Caps','Apps','Age','Reputation','Salary'] # 从上面图表可以看出转回费全是0,因此我们将其剔除
ks_result = {}
for f in feature3:ks_stats,p_value = stats.kstest(df2[f],'norm',args=(df2[f].mean(),df2[f].std()))print(f'{f}:KS statistic:{ks_stats},P-value:{p_value}.')
Caps:KS statistic:0.35329526602141725,P-value:0.0. Apps:KS statistic:0.15802018198153772,P-value:0.0. Age:KS statistic:0.08143107877963102,P-value:9.775470716540734e-236. Reputation:KS statistic:0.03507042116880876,P-value:5.033392897827099e-44. Salary:KS statistic:0.43688173742912745,P-value:0.0.
从这里可以看出P值没有高于0.05的,因此我们可以认为这些数据不符合正态分布,因此我们对相关性的分析可以使用斯皮尔曼
results = []
# 对连续型数据我们采用斯皮尔曼相关系数来判断其相关性
continuous_features = ['Caps','Apps','Age','Reputation','Salary']
for feature in continuous_features:corr,p_value = spearmanr(df2[feature],df2['Salary'])results.append({'Feature': feature, 'Spearman Corr': corr, 't-stat': None, 'ANOVA': None, 'p-value': p_value})# 对二分类数据我们采用t检验来判断其相关性
categorical_features = ['Is_top_5_League','Based_rich_nation','EU_National','Is_top_prev_club']
for feature in categorical_features:group0 = df2[df2[feature] == 0]['Salary']group1 = df2[df2[feature] == 1]['Salary']t_stat, p_value = ttest_ind(group0, group1)results.append({'Feature': feature, 'Spearman Corr': None, 't-stat': t_stat, 'ANOVA': None, 'p-value': p_value})# 对多分类数据我们采用方差分析来判断
anova_features = 'Is_top_ranked_nation'
group = [df2[df2[anova_features] == cat]['Salary'] for cat in sorted(df2[anova_features].unique())]
anova_stats,p_vlaue = f_oneway(*group)
results.append({'Feature':anova_features, 'Spearman Corr': None, 't-stat': None, 'ANOVA': anova_stats, 'p-value': p_value})df_results = pd.DataFrame(results)
df_results| Feature | Spearman Corr | t-stat | ANOVA | p-value | |
|---|---|---|---|---|---|
| 0 | Caps | 0.089277 | NaN | NaN | 5.846491e-73 |
| 1 | Apps | 0.517847 | NaN | NaN | 0.000000e+00 |
| 2 | Age | 0.249744 | NaN | NaN | 0.000000e+00 |
| 3 | Reputation | 0.833983 | NaN | NaN | 0.000000e+00 |
| 4 | Salary | 1.000000 | NaN | NaN | 0.000000e+00 |
| 5 | Is_top_5_League | NaN | -35.837645 | NaN | 5.814363e-277 |
| 6 | Based_rich_nation | NaN | -14.167243 | NaN | 1.873582e-45 |
| 7 | EU_National | NaN | -2.128449 | NaN | 3.330584e-02 |
| 8 | Is_top_prev_club | NaN | -33.013365 | NaN | 6.765112e-236 |
| 9 | Is_top_ranked_nation | NaN | NaN | 34.930631 | 6.765112e-236 |
出场次数与球员工资之间的斯皮尔曼相关系数为 0.089,表示两者之间有很弱的正相关性。 所有出场时间与球员工资之间的斯皮尔曼相关系数为 0.518,表明有中等程度的正相关性。 年龄与球员工资之间的斯皮尔曼相关系数为 0.250,显示两者间有较弱的正相关性。 影响力与球员工资之间的斯皮尔曼相关系数为 0.834,表明两者之间有较强的正相关性。 Is_top_5_League: t检验的t值为 -35.84,p值非常小,表明是否在在五大联赛效力与球员工资存在显著差异。 Based_rich_nation: t检验的t值为 -14.17,p值非常小,表示球员生活的国家是否富裕与球员工资之间存在显著差异。 EU_National: t检验的t值为 -2.13,p值为0.033,显示是否为欧洲国家与球员工资之间的差异在统计学上显著。 Is_top_prev_club: t检验的t值为 -33.01,p值非常小,显示前俱乐部球员是否曾在顶级俱乐部效力过与球员工资之间有显著差异。 Is_top_ranked_nation: 方差分析的F值为 34.93,p值非常小,表明球员所代表的国家是否在国际足联世界排名中名列前茅在不同组别中对球员工资有显著的影响。
模型的建立,由于部分数据跨度较大,因此我们先对数据进行标准化,之后计算VIF值,确定其不存在多重共线性。 这里我们又用到了多元线性回归模型,因此步骤还是老步骤,首先对残差进行正态性,独立性,同方差性进行检验
data = df2.copy()
data = data.drop('Last_Transfer_Fee',axis=1)
feature4 = ['Caps','Apps','Age','Reputation']
scaler = StandardScaler()data[feature4] = scaler.fit_transform(data[feature4])# 由于目标值不符合正态分布,因此我们对目标值进行对数变换,使其更加接近于正态分布
data['Log_Salary'] = np.log(data['Salary'])# 接下来我们计算各个特征的VIF值,确定其是否存在多重共线性
X = data.drop(['Salary','Log_Salary'],axis=1)
y = data['Salary']VIF_data = pd.DataFrame()
VIF_data['feature'] = X.columns
VIF_data['VIF_values'] = [variance_inflation_factor(X.values,i) for i in range(X.shape[1])]
VIF_data
| feature | VIF_values | |
|---|---|---|
| 0 | Is_top_5_League | 1.391285 |
| 1 | Based_rich_nation | 3.278526 |
| 2 | Is_top_ranked_nation | 3.251428 |
| 3 | EU_National | 3.027021 |
| 4 | Caps | 1.228038 |
| 5 | Apps | 3.205145 |
| 6 | Age | 2.970727 |
| 7 | Reputation | 1.429138 |
| 8 | Is_top_prev_club | 1.081392 |
可以看出VIF值基本都在1-4之间,因此我们可以判断出,数据中不存在多重共线性 接下来,我们开始对数据集进行建模
data.drop('Salary',axis=1,inplace=True)X = data.drop('Log_Salary',axis=1)
y = data['Log_Salary']X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=42)line_model = LinearRegression()
line_model.fit(X_train,y_train)
y_pred = line_model.predict(X_train)
residuals = y_train - y_predDW = durbin_watson(residuals)
print('DW值:',DW)DW值: 1.9994671572216502
这里可以看出DW值在2附近,因此我们可以看出线性回归的残差独立性是比较好的,接下来我们对残差的正态性和同方差性进行检验
# KS检验
ks_statistic,ks_pvalues = kstest((residuals - np.mean(residuals))/ np.std(residuals),'norm')
print(f'KS检验:{ks_statistic},P值:{ks_pvalues}')KS检验:0.029053858860392467,P值:2.2584717876590108e-21
# 增加常数项到自变量矩阵中,因为线性回归模型默认包含截距
X_constant = sm.add_constant(X_train)
# Breusch-Pagan检验
bp_test = het_breuschpagan(residuals,X_constant)
labels = ['Lagrange multiplier statistic', 'p-value', 'f-value', 'f p-value']
print(dict(zip(labels, bp_test))){'Lagrange multiplier statistic': 1643.1994698959277, 'p-value': 0.0, 'f-value': 193.65865696721104, 'f p-value': 0.0}
从P-value可以看出,残差并没有通过同方差性检验,因此我们就不使用多元线性回归模型来进行预测了 因此我们接下来使用随机森林来进行预测
Rtree = RandomForestRegressor()
Rtree.fit(X_train,y_train)y_pred = Rtree.predict(X_test)
R2 = r2_score(y_test,y_pred)print('R2系数:',R2)R2系数: 0.7949048167355701
important_feature = Rtree.feature_importances_
feature = X.columnssort_index = important_feature.argsort()plt.figure(figsize=(12, 6))
plt.barh(range(len(sort_index)), important_feature[sort_index])
plt.yticks(range(len(sort_index)), [feature[i] for i in sort_index])
plt.xlabel('特征重要性')
plt.title('特征重要性分析')plt.show()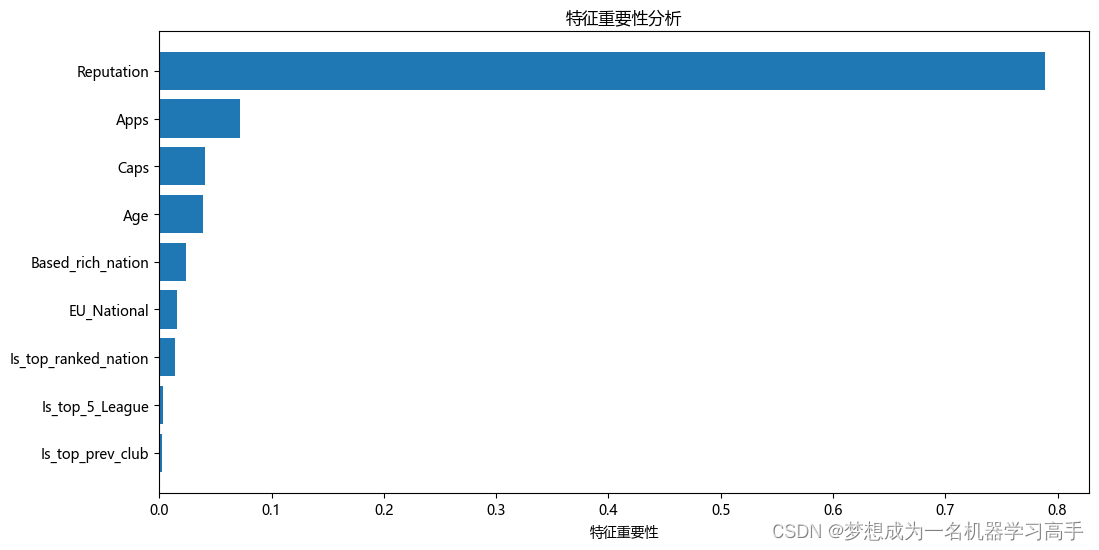




![[C/C++] -- 代理模式](https://img-blog.csdnimg.cn/direct/c137906aa12e46f6ad78fd8a5ab60e2e.png)