什么是递归

下面引用刘汝佳的《算法竞赛入门经典》中对递归的定义：

• 递归：参见递归。
• 递归：如果你还不理解递归是什么，请参见递归。

递归事实上就是函数直接或间接调用自身的一个过程。（或者其它本质上相似过程的也可以称为递归。）但和许多基本的概念一样，定义总是很简洁，但真正运用起来却并不容易。
在程序设计中为了保证递归能够结束，递归函数一定需要一个结束条件，称这个条件为基线条件，满足基线条件时停止递归调用。

递归和栈

程序的执行有严格的顺序，不考虑并行算法的话，一个程序在某一时刻只能处理一条语句（或者说是不可能有两个计算的过程同时执行）。递归函数自然也是按一定顺序执行的。
函数调用函数的过程形成一个栈结构，称为调用栈。

需要清楚：

1. main()函数一定位于栈底
2. 每调用一个函数，就将这个函数压入栈中
3. 计算机当前处理的语句位于栈顶的函数中
4. 当一个函数完全执行结束时（完全执行结束意味着这个函数调用的函数也已经执行结束），将这个函数从栈顶弹出。
5. 递归函数在达到基线条件之前，递归函数是不断进行栈的压入，到达基线条件之后递归函数不断进行栈的弹出，直到到达递归入口
6. 当main()函数从栈中弹出时，整个程序运行结束

由于递归函数不断地进行调用，通常递归函数容易产生层数较多的调用栈。递归函数一定可以使用一般的栈结构来模拟出来。

尾递归

尾递归是指容易用简单循环语句转化为非递归算法的一种递归。有时尾递归更类似于一种递推方法，例如求阶乘函数的尾递归写法：

int fun(int x,int ans=1){ if(x<=1)    return ans;else return fun(x-1,ans*x);
}
相当于函数：int fun(int x){int ans=1;for(int i=x;i>1;i--)    ans=ans*i;return ans;
}
而阶乘函数的非尾递归写法：int fun(int x){if(x<=1)    return 1;else return fun(x-1)*x;
}

通过对比尾递归和非尾递归的两种写法，不难发现尾递归算法在满足基线条件时就已经得到了想要的结果，而非尾递归算法满足基线条件时不能直接得到最终结果，而是将返回的值传递给上一层的递归函数，让上一层函数继续处理。有些地方对尾递归的定义中写道尾递归是可以转化为循环语句的递归，而其它递归是可以用栈来模拟的递归，这样的说法是不正确的，因为只要是递归，就可以使用栈来模拟。只是有时会复杂一些。

递归和分治

分治算法即不断划分子问题，最后合并的算法。容易得到分治的两个重点在于：

• 划分
• 合并子问题

由于分治算法划分的子问题一般具有相同的结构，也就具有相似的解决方案。所以很显然递归的思想可以用来实现分治算法。值得一提的是，划分子问题是为了利用子问题的结果得到合并后的那个问题的结果。即递归的上一层需要用到该层的结果，因此分治算法不属于尾递归算法。或者说可以用尾递归算法解决的问题不需要分治。

归并排序

归并排序是分治算法的一个典型的例子。

归并排序的基本思想在于：

如果一个数组的前半部分和后半部分都是有序的，那么就可以使用二路归并的方法将前半部分与后半部分合并，时间复杂度$O(n)$。
由第一条可以想到把一个数组中所有元素排序，可以先将元素分成相等的两部分排序，再按上一条的方法合并。

归并排序的代码：

void merge_sort(vector<int> &V){if(V.size()<=1) return;vector<int> A;vector<int> B;for(int i=0;i<V.size()/2;i++)   A.push_back(V[i]);for(int i=V.size()/2;i<V.size();i++)    B.push_back(V[i]);merge_sort(A),merge_sort(B);//二路归并，此时A和B都已经排过序V.clear();int p1=0,p2=0;while(p1<A.size()||p2<B.size()){if(p1>=A.size())    V.push_back(B[p2]),p2++;else if(p2>=B.size())   V.push_back(A[p1]),p1++;else{if(A[p1]<B[p2]) V.push_back(A[p1]),p1++;else V.push_back(B[p2]),p2++;}}
}

可以看到归并排序的函数中有两条调用自身的语句。这时称这个函数可以形成最多两条分支。当元素个数为10时归并排序的分支结构可以形象的表示为下图：

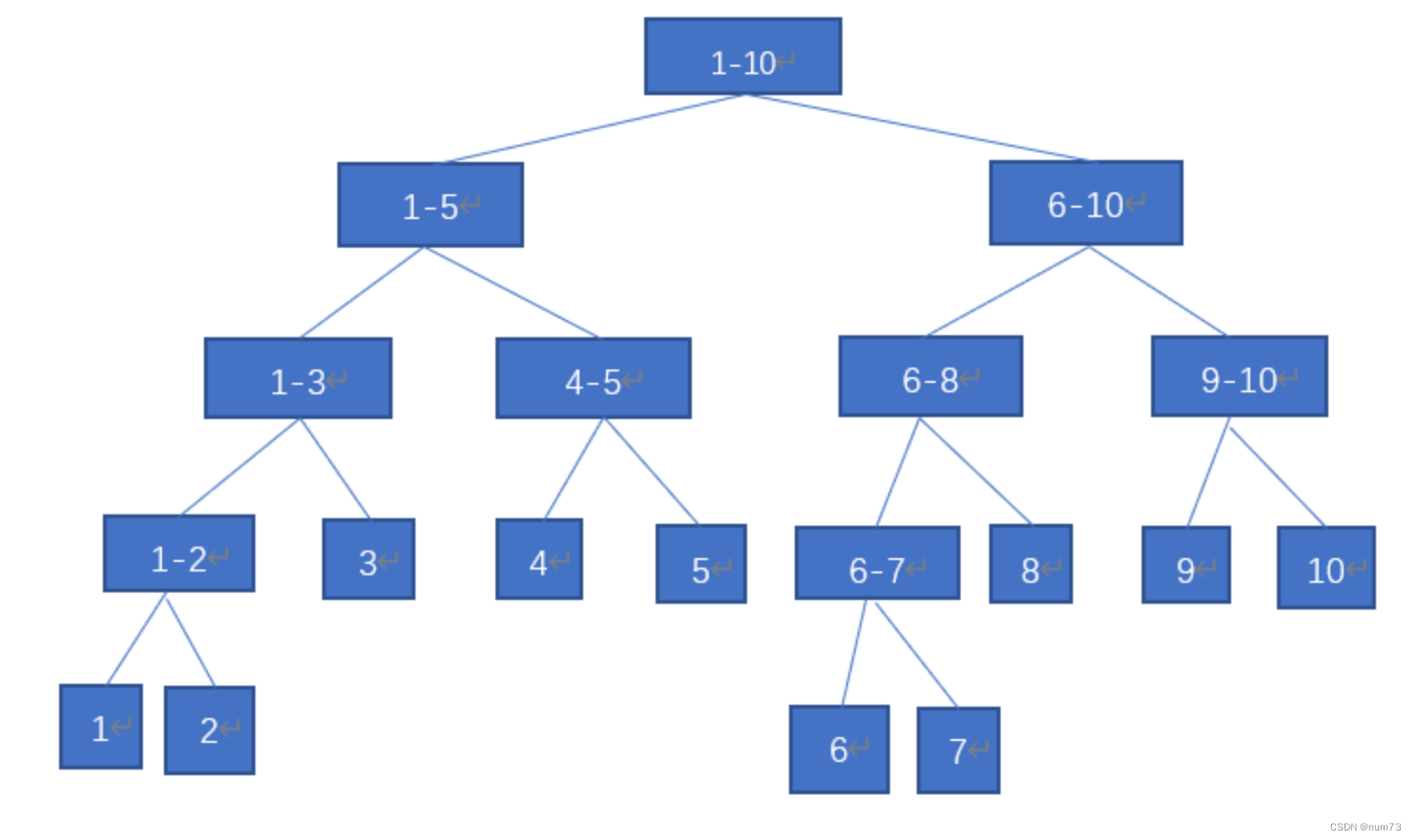
像这样的表示递归过程的图像可以称为解答树。将递归过程中由于递归产生栈的最大的层数成为递归的层数，很显然上图表示的过程层数为5。可以证明归并排序的层数不会超过$logn+2$，而每一层处理都需要$O(n)$的时间，所以归并排序的时间复杂度为$O(nlogn)$。
用递归的层数乘以每层需要的时间也是分析递归函数时间复杂度的常用手段

递归和树

树是无环图。把树的一条边去掉，得到的两个部分仍然是树结构。或者可以说树可以由两个树通过一条边相连构成。

于是我们也可以用下面的方法定义树：

• 一个点是一棵树
• 两个树通过一条边相连得到的仍然是一棵树

树的定义是递归的，所以树结构用递归来处理最为合适。
用递归用来处理树的最常见的例子就是树的搜索，也叫树的遍历。有时也称作DFS（深度优先搜索）或BFS（广度优先搜索）。