给定一个不含重复数字的整数数组
nums,返回其 所有可能的全排列 。可以 按任意顺序 返回答案。输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
先在这里说明一下排列和组合的区别?
组合:是指从一个元素集合中选择出若干个元素,形成一个无序的子集,组合不考虑元素的顺序,只关注元素的选择
排列:是指从一个元素集合中选择出若干元素,形成一个有序的序列。排列关注元素的顺序。
简单的来说,就是排列是元素是有序的,组合是无序的
一般排列组合问题我们都可以看成是一棵树(每个元素不允许重复)
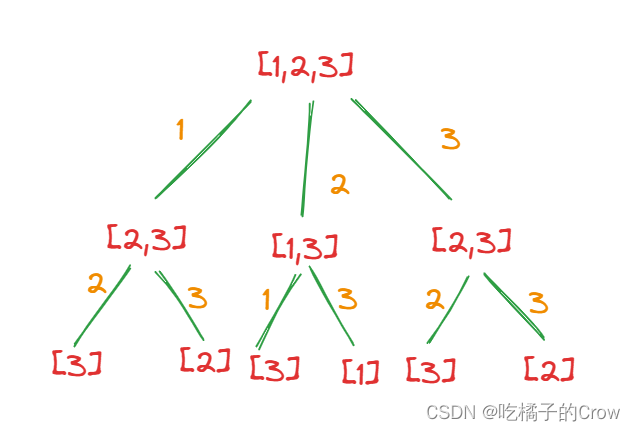
因为我们这题要求的是不重复的排列数,所以我们的模板就可以套了(模板必须要记的——理解)
//不含重复元素的排列数
void backTrack(int[] nums){1for(int i=0;i<nums.length;i++){if(uesd[i])continue;used[i]=true;path.addLast(nums[i]);backTrack(nums);path.removeLast(nums[i]);used[i]=false;}源代码如下:
//存储结果集List<List<Integer>> list = new ArrayList<>();//路径Deque<Integer> path = new LinkedList<>();//是否被访问boolean[] visited = null;public List<List<Integer>> permute(int[] nums) {//对入参进行判断if (nums == null || nums.length == 0) {return list;}//对数组进行初始化visited=new boolean[nums.length];//开始递归,因为是排列,后面的元素也有可能在前面的元素前面,所以不需要传递索引backtracking(nums);//返回结果集return list;}private void backtracking(int[] nums) {//找到满足条件得到一种情况,存入结果集中if (path.size()== nums.length) {list.add(new ArrayList<>(path));return;}//遍历每一个元素for (int j = 0; j < nums.length; j++) {//如果被访问过,直接跳过,避免重复选择if(visited[j]){continue;}path.add(nums[j]);visited[j]=true;backtracking(nums);//回溯path.removeLast();visited[j]=false;}
}在这里给大家提供我刷组合排列问题总结的模板:
组合子集问题每个元素的相对位置已经固定,所以每次去枚举的时候都是从自身的右侧开始枚举
排列问题的每个元素的相对位置是不固定的。左侧的元素可能会出现在右侧,故每次每次枚举都是从0位置上开始枚举的
-
元素无重不可复选(nums中的元素唯一,每个元素最多只能被使用一次)
/*组合/子集问题回溯模板*/
/* [1,2,3] */
void backTrack(int[] nums,int start){//顺序无关,每次从自身的右边开始for(int i=start;i<nums.length;i++){path.addLast(nums[i]);backTrack(nums,i+1);path.removeLast(nums[i]);}
}
/* 排列问题回溯模板*/
void backTrack(int[] nums){//顺序有关,每次从0开始for(int i=0;i<nums.length;i++){if(uesd[i])continue;used[i]=true;path.addLast(nums[i]);backTrack(nums);path.removeLast(nums[i]);used[i]=false;}
}-
.元素可重不可复选(nums中的元素可以存在重复,每个元素最多只能被使用一次)
Arrays.sort(nums); /* 组合/子集问题回溯算法框架 */ void backtrack(int[] nums, int start) {// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 剪枝逻辑,跳过值相同的相邻树枝if (i > start && nums[i] == nums[i - 1]) {continue;}// 做选择track.addLast(nums[i]);// 注意参数backtrack(nums, i + 1);// 撤销选择track.removeLast();} }Arrays.sort(nums); /* 排列问题回溯算法框架 */ void backtrack(int[] nums) {for (int i = 0; i < nums.length; i++) {// 剪枝逻辑if (used[i]) {continue;}// 剪枝逻辑,固定相同的元素在排列中的相对位置if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue;}// 做选择used[i] = true;track.addLast(nums[i]);backtrack(nums);// 撤销选择track.removeLast();used[i] = false;} }
有很多人对上述剪枝操作不理解,看了这幅图你就会豁然开
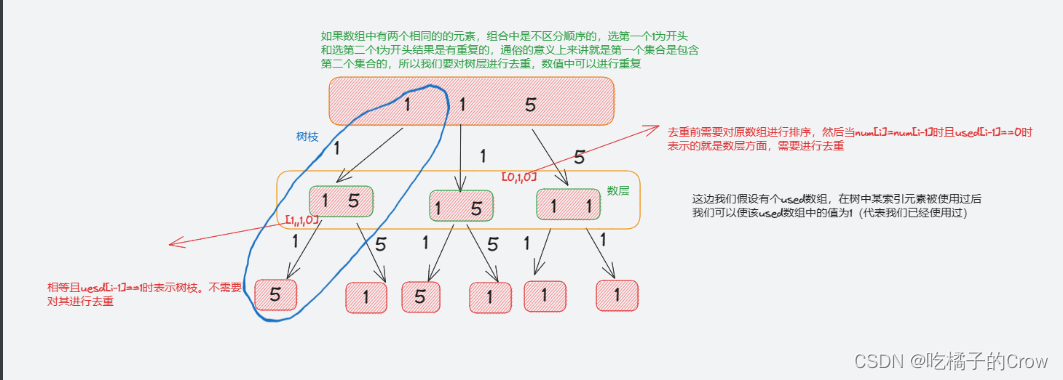
-
元素无重可复选(nums中的元素都是唯一的,每个元素可以被使用若干次)
/* 组合/子集问题回溯算法框架 */ void backtrack(int[] nums, int start) {// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 做选择track.addLast(nums[i]);// 可以复选,所以i不用+1作为参数backtrack(nums, i);// 撤销选择track.removeLast();} }/* 排列问题回溯算法框架 */ void backtrack(int[] nums) {for (int i = 0; i < nums.length; i++) {// 做选择track.addLast(nums[i]);backtrack(nums);// 撤销选择track.removeLast();} }