深度学习笔记001-编程知识

一、批量规范化

二、残差网络ResNet

三、稠密连接网络（DenseNet）

四、循环神经网络

五、信息论

六、梯度截断

本篇blog仅仅是本人在学习《动手学深度学习 Pytorch版》一书中做的一些笔记，感兴趣的读者可以去官网http://zh.gluon.ai/

这里主要是记录个人对一些概念的理解，仅此而已。存在错误欢迎指出。

一、批量规范化

主要是用来加速深层网络的收敛速度。因为在从输入到训练的过程中，模型的参数变化是难以预测的，这种变化在深层网络中被非正式的假设会阻碍网络的收敛，所以在每一次迭代中，我们对其进行标准化，即使用这种标准化进行补偿在训练过程中变量分布的偏移和拉伸。

$BN(x)=\gamma \odot \frac{x-\mu _{B}}{\sigma _{B}}+\beta$

B为小批量样本（批量的大小设置比没有使用批量规范化更加重要），其中的 $\mu _{B}$ 和 $\sigma _{B}$ 是小样本的样本均值和样本标准差。其中的 $\gamma ,\beta$ 是拉伸参数和偏移参数，需要和模型一同训练。

使用：在全连接层中，批量规范化一般是加在仿射变换和激活函数之间；在卷积层中，一般是加在卷积层后和非线性激活函数之间，注意输入的大小是相同的。

net = nn.Sequential(nn.Conv2d(1,6,kernel_size=5),nn.BatchNorm2d(6),nn.Sigmoid(),nn.AvgPool2d(kernel_size=2,stride=2),nn.Flatten(),nn.Linear(36,10),nn.BatchNorm1d(10),nn.Sigmoid(),nn.Linear(10,2))

注意这里的BatchNorm2d 和BatchNorm1d。2d是针对卷积层的规范化，1d是针对全连接层的规范化。

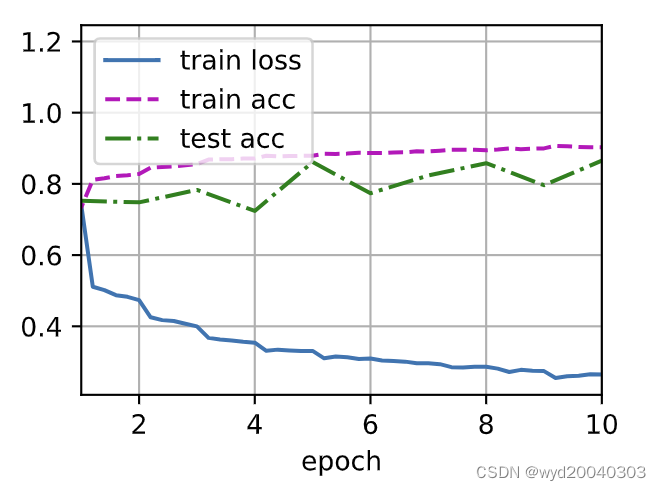
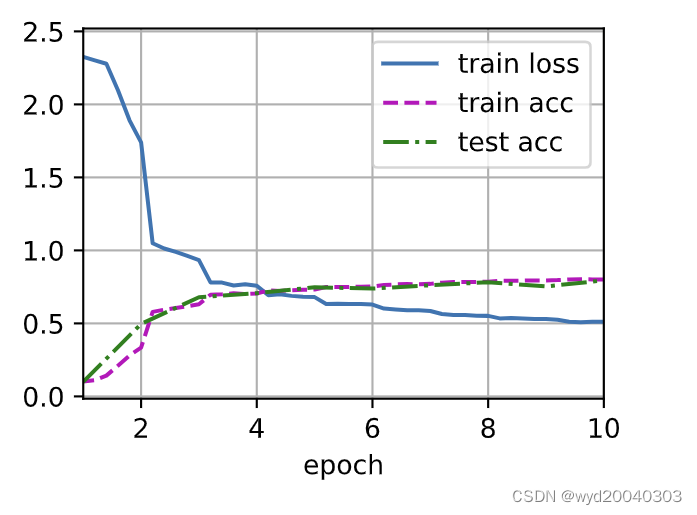
二、残差网络ResNet

在神经网络架构 $F$ 上很难找到真正的函数 $f$ ，因此想要修改通过改进 $F$ 的网络架构以此来优化。但是如果 $F$ 的架构并非是嵌套的，则会导致高阶 $F$ 会远离目标函数。

只有当 $F$ 之间是相互嵌套的才能满足。残差网络就是来解决这个问题的。

残差网络涉及到了几个问题。对于理想的映射 f(x)，在输入x后将x引入一个正反馈到输出的激活函数前，这样该网络只需要学习 f(x)-x这个残差映射就行。

残差网络能够用来简化深层网络训练问题，是因为它通过引入残差学习框架，将网络层重新表述为相对于层输入的残差函数，而不是学习无参考的函数。这样也使得网络更加容易优化，应该它学习的不是整个映射。

同时，残差网络也更好的解决了深层网络梯度消失的问题。在深度网络中，梯度消失是一个常见的问题，特别是在训练深层网络时。残差学习通过跳跃连接（skip connections）的方式，使得梯度能够更快地传播到浅层，从而减少了梯度消失问题的影响。

三、稠密连接网络（DenseNet）

稠密连接网络是ResNet网络的扩展，是将每一层的信息直接传给后面的所有层。和残差网络不同的是，残差网络使用的是直接相加的方式，而稠密网络使用的是连接的方式。

稠密连接的优势在于：

信息流更加充分：稠密连接网络中的每一层都直接连接到后面所有的层，使得信息能够从网络的前部流动到后部，避免了信息在深层网络中逐渐丢失的问题。这种密集的连接结构使得网络更加容易捕获和传递输入数据的信息，有助于提高模型的表示能力。
梯度更加稳定：由于每一层都直接连接到后面所有的层，稠密连接网络中的梯度可以更容易地通过网络反向传播。这有助于缓解梯度消失或梯度爆炸的问题，使得模型更容易训练。
参数共享：稠密连接网络中的每一层都可以访问前面所有层的特征图，因此可以在每一层中共享参数。这样可以大大减少模型的参数量，降低了过拟合的风险，并提高了模型的效率。
网络更深：稠密连接网络中的稠密连接结构使得网络更容易训练，因此可以构建更深的网络。更深的网络通常具有更强的表示能力，可以学习到更复杂和抽象的特征表示，从而提高模型的性能。

其使用情景在于：

小数据集的时候，通过参数重用和参数共享来降低过拟合的风险。