这里的知识来自于论文 Delving into the Devils of Bird’s-eye-view Perception: A Review, Evaluation and Recipe 的 Appendix B.1
部分来自 这篇文章

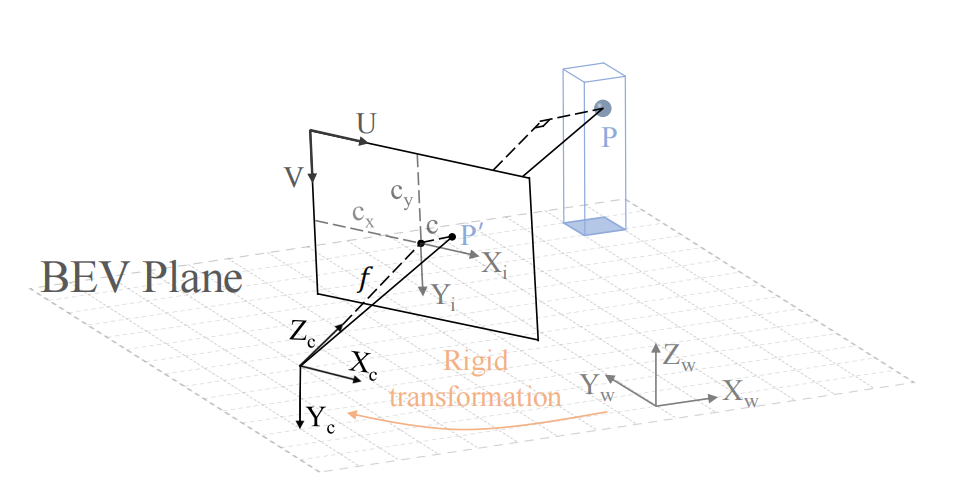
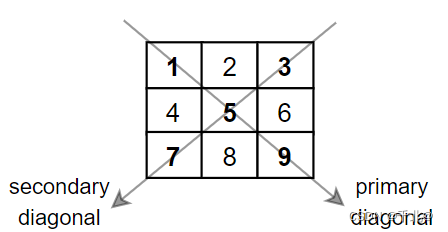
从透视图转向鸟瞰图。（Xw、Yw、Zw）、（Xc、Yc、Zc）表示世界World坐标和相机Camera坐标，$（X_i、Y_i）$、（U、V）表示图像坐标和像素坐标。由于图像坐标系和像素坐标系处于同一平面，故两者之间的差异在于坐标原点的位置和单位。像素坐标系的原点在图像坐标系的左上角，同时像素坐标系的单位为像素。
故两个坐标系之间的变换满足
$u=\frac{x}{d_x}+u_0，v=\frac{y}{d_y}+v_0$
dx，dy表示像素坐标系中每个像素点的宽和高，而图像坐标系原点在像素坐标系中的横纵坐标分别为 $u_0,v_0$。
从BEV平面上升起一根柱子。P代表柱子上的3D点，$P^{{}^{\prime }}$代表P相应在相机视角上的投影点。
P，$P^{{}^{\prime }}$分别对应于柱上的三维点和摄像机视图上投影的2D点。
给定P的世界坐标和相机的内在参数和外在参数，可以得到$P^{{}^{\prime }}$的像素坐标。

显式BEV特征构造通常需要基于三维到二维投影对局部图像视图特征进行索引。上图显示BEVFormer的视角转换。一根柱子从BEV平面升起，柱子内的一个三维点被投影到相机视图上。
投影过程涉及到世界World、相机Camera、图像Image和像素Pixel坐标系之间的转换。
从世界坐标到相机坐标的转换是一种刚性变换，只需要平移和旋转（更详细的可以看上面的博客）。
设$P_w=[x_w、y_w、z_w，1]、P_c=[x_c、y_c、z_c，1]$分别为一个三维点P在世界坐标和相机坐标中的同质表示。它们之间的关系可以描述如下：
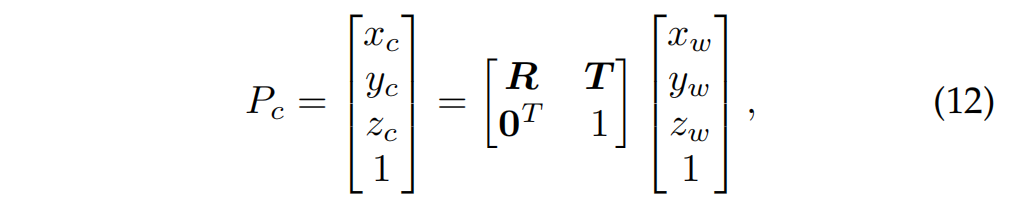R，T分别表示旋转矩阵和平移矩阵。