回溯算法—组合问题-编程知识

文章目录

介绍
应用问题
基本流程
算法模版
例题
- （1）组合
- （2）电话号码的字母组合

介绍

回溯算法实际上是一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

应用问题

组合问题：N个数里面按一定规则找出k个数的集合
子集问题：一个N个数的集合里有多少符合条件的子集
切割问题：一个字符串按一定规则有几种切割方式
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

基本流程

选择：在当前步骤中，从可选的选择中选择一个。
验证：检查选择是否满足问题的约束条件和限制。
递归：进入下一步骤，继续选择和验证。
撤销：如果选择不满足问题要求，回溯到上一步，撤销当前选择，并尝试其他选择。

回溯法解决的问题都可以抽象为树形结构

集合的大小就构成了树的宽度，递归的深度就构成了树的深度。

算法模版

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

递归嵌套for循环

回溯三部曲：

递归函数的参数和返回值：返回值一般为void
确定终止条件
单层搜索的逻辑

例题

（1）组合

77. 组合 - 力扣（LeetCode）

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：
输入：n = 4, k = 2
输出：
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]

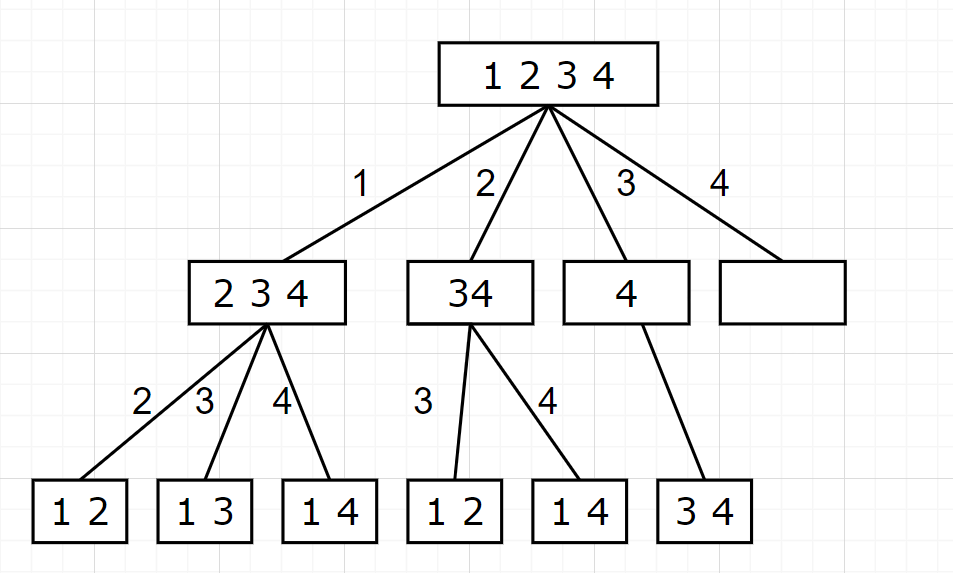
组合是无序的，[1,2]和[2,1]一致

每一个节点都是一层for循环，从startIndex开始

递归函数的参数和返回值：

void backTracking(int n, int k, int startIndex)

确定终止条件

到达叶子节点，path数组大小到达k
```
if (pathtop == k) 
```
单层搜索的逻辑

for循环从startIndex到n中选择数字（startIndex控制每次搜索时的起始位置，本题第一次调用时传1）

先处理当前i节点；
再递归：传入i+1控制下一层递归起始位置；
回溯：退出递归调用之后，需要回溯到之前的状态，来尝试其他数字并构建其他组合。因此 pathtop 减 1，i + 1退出递归后在当前循环还是i。
```
for (int i = startIndex; i <= n; i++) {path[pathtop++] = i; // 存入结果backTracking(n, k, i + 1); // 递归，传入i+1，下一层递归起始位置pathtop--;
}
```
for循环横向遍历，递归纵向遍历，回溯不断调整结果集

int* path;
int pathtop;
int** ret;
int rettop;
void backTracking(int n, int k, int startIndex) {if (pathtop == k) {int* temp = (int*)malloc(sizeof(int) * k);for (int i = 0; i < k; i++) {temp[i] = path[i];}ret[rettop++] = temp;return;}for (int i = startIndex; i <= n; i++) {path[pathtop++] = i;backTracking(n, k, i + 1);pathtop--;}
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {pathtop = 0;rettop = 0;path = (int*)malloc(sizeof(int) * k);ret = (int**)malloc(sizeof(int*) * 1000000);backTracking(n, k, 1);*returnSize = rettop;(*returnColumnSizes) = (int*)malloc(sizeof(int) * (*returnSize));for (int i = 0; i < (*returnSize); i++) {(*returnColumnSizes)[i] = k;}return ret;
}

剪枝

时间复杂度：叶子个数乘叶子到根的路径长度

for循环在寻找起点的时候要有一个范围，如果这个起点到集合终止之间的元素已经不够题目要求的k个元素了，就没有必要搜索了

例如如果n = 4, k = 4情况下

nk4

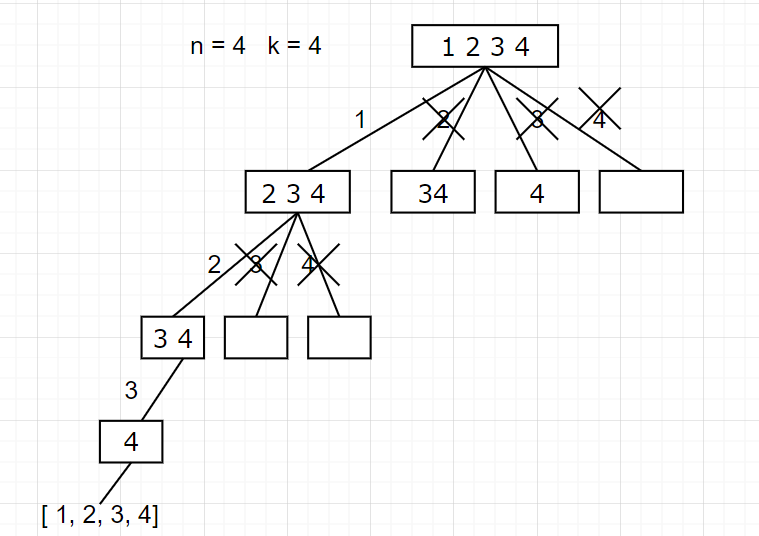
已经选择的数量：pathTop

还需要选择的数量：k - pathTop

集合n中至多要从n - (k - pathTop) + 1 开始遍历

[1,2,3,4]

n=4,k=3,假设选了一个了，还要选两个，那么至多从n - 2 + 1 = 3，

假设选了0个，那么还要选三个，那么至多从n - 3 + 1 = 2，

 for (int i = startIndex; i <= (n - k + pathtop + 1); i++) {path[pathtop++] = i;backTracking(n, k, i + 1);pathtop--;}

（2）电话号码的字母组合

17. 电话号码的字母组合 - 力扣（LeetCode）

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
示例 1：
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2：
输入：digits = ""
输出：[]

递归函数的参数和返回值：

void backTracking(char* digits, int length, int index)

确定终止条件

遍历到字符串末尾
```
 if (pathTop == length) 
```
单层搜索的逻辑

创建一个map[10][5] 来存储不同号码对应的字母

for循环遍历的是map[i] 的长度

char** ret;
int retTop;
char* path;
int pathTop;
char map[10][5] = {"\0",    "\0",    "abc\0",  "def\0", "ghi\0","jkl\0", "mno\0", "pqrs\0", "tuv\0", "wxyz\0"};
void backTracking(char* digits, int length, int index) {// 当遍历到字符串末尾时，将当前组合加入结果集中if (index == length) {char* temp = (char*)malloc(sizeof(char) * (pathTop + 1));memcpy(temp, path, sizeof(char) * pathTop);temp[pathTop] = '\0';ret[retTop++] = temp; return;}// 获取当前数字对应的字符集合的长度int num = digits[index] - '0';int letterLength = strlen(map[num]);// 遍历当前数字对应的字符集合for (int i = 0; i < letterLength; i++) {// 当前组合长度达到字符串长度时，退出循环if (pathTop >= length) {break;}// 将当前字符加入当前组合中path[pathTop++] = map[num][i];backTracking(digits, length, index + 1);pathTop--;}
}// 主函数，生成数字键盘对应的所有字母组合
char** letterCombinations(char* digits, int* returnSize) {retTop = pathTop = 0;int maxPathLength = strlen(digits) * 4; path = (char*)malloc(sizeof(char) * (maxPathLength + 1));ret = (char**)malloc(sizeof(char*) * 1000);// 初始化结果集数组为空for (int i = 0; i < 1000; ++i) {ret[i] = NULL;}int length = strlen(digits);// 输入字符串长度为0返回空结果集if (length == 0) {*returnSize = 0;return ret;}backTracking(digits, length, 0);*returnSize = retTop; return ret; 
}