【物理】功与能
功
基础概念
定义
一个物体在力的作用下,沿力的方向,通过一段距离(位移),则称这个力做了功。
公式
功的定义式:
这里的 \(x\) 指的是物体沿力的方向上发生的位移。由于力 \(F\) 和位移 \(x\) 都是矢量,所以得到的功 \(W\) 是标量。
注意:虽然 \(W\) 是标量,但是 \(\pu{-5 J > 3 J}\),因为这里的负号表示做负功,或阻力做功。即对于所有变量,都按照数轴从左到右依次增大,功除外。
功的计算式:
这里的 \(x\) 指的是实际位移,\(\theta\) 表示力与位移的夹角。功的单位是焦耳,字母表示为 \(\pu J\)。
例:如下图所示,一物体从斜面顶端滑到斜面底端,问重力做的功是多少。

求解:
根据题意可知
这道题中涉及了两个计算功的方法:
- 功的计算式,即 \(W = Gc \cos \angle 2\),这里的 \(c\) 指的是实际位移。
- 功的定义式,即 \(W = Gb\),这里的 \(b\) 指的是在力的方向上发生的位移。
对于功的计算式中 \(\theta\) 的理解:
首先如下图所示:

对于 \(F\) 在 \(x\) 方向上做的功,那么考虑将 \(F\) 沿图中建系得到的两个方向分解为 \(F_x\) 和 \(F_y\),那么
\[W_F = W_x + W_y = F \cos \theta \cdot x + 0 = Fx \cos \theta \]由于在 \(y\) 方向上位移为 \(0\),所以 \(W_F = W_x = Fx \cos \theta\)。
计算
恒力做功计算
求大小方向恒定的力做功(例如重力),一般有以下两种思路:
若物体做直线运动,则使用力的「计算式」,即 \(W = Fx \cos \theta\),\(x\) 表示实际位移。
若物体做曲线运动,则使用力的「定义式」,即 \(W = Fx\),\(x\) 表示在力的方向上的位移。
注意:求 \(F\) 可能需要通过受力分析求出。
例:如图所示,一质量为 \(m\) 的小球,用长为 \(L\) 的轻绳悬挂于 \(O\) 点,小球在水平力恒力 \(F\) 作用下,从 \(P\) 点移到 \(Q\) 点,此时悬线与竖直方向夹角为 \(\theta\),则求重力做的功是多少。

分析:
由于物体做曲线运动,所以考虑使用功的「定义式」,那么
这里力的方向上的位移是 \(x = L - L \cos \theta\),这是常见的计算位移的方式。且由于物体位移向上,而重力向下,所以功是负功,这里需要注意功的正负。
变力做功计算
特殊情况:
若变力的方向与位移方向(速度方向)始终垂直,说明在力的方向上没有位移,所以不做功,即 \(W_F = 0\)。例如物体做圆周运动时提供向心力的力始终与速度方向垂直,不做功。
若变力只有方向改变、大小不改变(例如某些情况下的滑动摩擦力),可以通过 \(W_F = Fs \cos \theta\) 计算,其中 \(s\) 表示物体经过的路程,\(\theta\) 表示 \(F\) 与 \(s\) 的夹角。此时,\(F\) 与 \(s\) 的夹角一般始终保持固定,且一般情况下题目中二者的夹角大部分都是 \(0^\circ\) 或 \(180^\circ\)。
一个较为典型的例子:
考虑一物体在粗糙水平面上,向右以初速度 \(v_0\) 的速度做直线运动,从某个起始点 \(A\) 运动到 \(B\) 然后折返回来到 \(A\)。整个过程中,物体始终受到一个向左的外力 \(F\),大小始终不变。物体从 \(A\) 到 \(B\) 再回到 \(A\) 的过程中,外力 \(F\) 做的功整体上是多少,滑动摩擦力 \(f\) 做的功整体上是多少。
分析:
首先对于外力 \(F\),属于大小方向均不变的恒力:
- 当物体由 \(A\) 运动到 \(B\) 的过程中,\(F\) 与位移方向相反,做负功,这个过程 \(W_F = - F x_{AB}\);
- 当物体由 \(B\) 折返回到 \(A\) 的过程中,\(F\) 与位移方向相同,做正功,这个过程 \(W_F = F x_{AB}\)。
那么两段路程做的功正负抵消,所以对于整个过程,外力 \(F\) 做功为 \(0\)。
然后对于滑动摩擦力 \(f\):
- 当物体由 \(A\) 运动到 \(B\) 的过程中,此时 \(f\) 与位移方向相反,做负功,这个过程 \(W_f = - f x_{AB}\);
- 当物体由 \(B\) 折返回到 \(A\) 的过程中,\(f\) 与位移方向依然相反,做负功,这个过程 \(W_f = - f x_{AB}\)。
那么对于整个过程,滑动摩擦力 \(f\) 做功为 \(W_f = - 2 f x_{AB}\)。
若变力只有大小改变,方向不改变,则可以考虑图象法。绘制 \(F-x\) 的图象,此时图象围成的面积表示功 \(W_F\)。图象在 \(x\) 轴上方的部分,\(F\) 做正功;图象在 \(x\) 轴下方的部分,\(F\) 做负功。则直接根据图象求出对应面积即可求出功。
例:如图所示,某个力 \(F\) 大小等于 \(\pu{200 N}\) 保持不变,作用在半径为 \(\pu{2 m}\) 的转盘边缘,方向时刻与此时的运动方向相同,当转盘转动一周时,力 \(F\) 做了多少功?

分析:
由于大小不变的力 \(F\) 的方向时刻与运动方向相同,所以 \(\theta = 0^\circ\),那么
总结:本题属于变力满足方向改变,大小不变的题型,且 \(F\) 与 \(s\) 夹角始终不变且已知,所以考虑 \(W = F s \cos \theta\)。求解思想是微元法。
功的正负判断
判断依据
根据 \(W = Fx \cos \theta\) 可知:
- 当 \(0^\circ \le \theta < 90^\circ\) 即力与位移夹角为锐角时,\(\cos \theta > 0\),功为正。
- 当 \(90^\circ < \theta \le 180^\circ\) 即力与位移夹角为钝角时,\(\cos \theta < 0\),功为负;
- 当 \(\theta = 90^\circ\) 即力与位移方向垂直时,\(\cos \theta = 0\),不做功。
常见力做功的正负
摩擦力
对于单个摩擦力可能做正功、负功,也可能不做功,下面是一些常见情形:
- 静摩擦力做正功:人握着话筒往上移动。
- 静摩擦力做负功:人握着话筒往下移动。
- 静摩擦力不做功:人握着话筒静止不动。
- 滑动摩擦力做正功:将一物体以初速度为 \(0\) 放在正在运行的传送带上的初始状态。
- 滑动摩擦力做负功:在地上滑行的物体。
- 滑动摩擦力不做功:擦黑板,摩擦力对黑板不做功(对板擦做功)。
对于一对摩擦力:
- 一对静摩擦力:互为相互作用力,大小相同,方向相反,位移相同,考虑做功正负抵消,所以做功之和一定为 \(0\)。
- 一对滑动摩擦力:做功之和一定小于 \(0\)。(具体解释涉及到能量,这里不做赘述。)
相互作用力
误区:一个作用力做正功,另一个作用力一定做负功。
解释:由于一对相互作用力作用到的物体不是同一个物体,而是两个不同的物体,所以无法直接预估做功的正负。
下面是一些常见的情形(例如「一正一负」表示一个作用力做正功,另一个作用力做负功):
- 一正一负:两块磁铁,一左一右,左往左动,右往左动。
- 一正一正:两块磁铁,一左一右,左往左动,右往右动。
- 一正一零:两块磁铁,一左一右,左往左动,右不动。
- 一负一负:两块磁铁,一左一右,左往右动,右往左动。
- 一负一零:两块磁铁,一左一右,左往右动,右不懂。
- 一零一零:两块磁铁,一左一右,都不动。
重力
重力做功的正负与高度有关:
- 高度变高:重力做负功。
- 高度变低:重力做正功。
- 高度不变:重力做功为 \(0\)。
合外力
根据合外力 \(F\) 的方向与加速度 \(a\) 的方向相同,位移 \(x\) 的方向与速度 \(v\) 方向相同可知:
- 速度变大:加速运动,\(a,v\) 同向,\(F,x\) 同向,合外力做正功。
- 速度变小:减速运动,\(a,v\) 异向,\(F,x\) 异向,合外力做负功。
- 速度不变:合外力不做功。
平衡力
一对平衡力做功,大小相等,方向相反,作用在同一个物体上,所以二者做功一正一负,根据同一个物体可知位移相同所以大小相同,做功之和一定为 \(0\)。
【经典题型】敲钉子做功的计算
问题模型:
用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比,即 \(F_f = kx\)(其中 \(x\) 为铁钉进入木块的深度),在铁锤击打第一次后,铁钉进入木块的深度为 \(d\)。则:
- 求铁锤对铁钉做功的大小。
- 若铁锤对铁钉每次做功都相等,求击打第二次时,铁钉还能进入的深度。
求解方法:图象法。
分析:
对于第一问,发现木块对铁钉的阻力 \(F_f\) 实际上方向不变,只有大小改变,那么考虑图象法,绘制 \(F_f-x\) 图象求解,如下图所示。
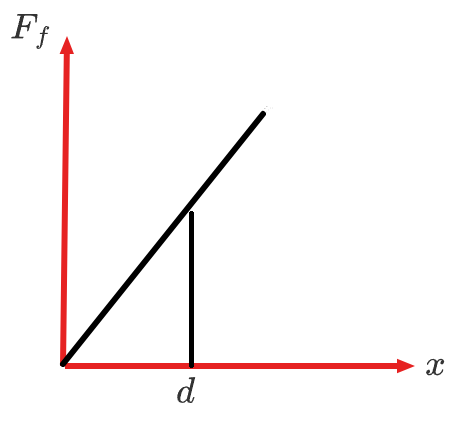
那么图中三角形围成的面积即为铁锤对铁钉做功的大小,所以
对于第二问:
假设击打第二次时,铁钉此时的深度为 \(d'\)。根据下图可知 \(S_1 = S_2\)。

根据相似三角形可知:
所以铁钉还能进入的深度 \(\Delta d = (\sqrt 2 - 1) d\)。
功率
基础概念
定义
功率是描述做功快慢的物理量。功率越大,做功越快。
公式
功率的定义式:
单位:焦耳每秒 \(\pu{J*s-1}\) 或瓦特 \(\pu W\)。功率是标量。定义式中的功率表示的是平均功率,即平均每秒做功的多少,例如 \(\pu{5 s}\) 内的平均功率。
功率的计算式:
计算式中的功率表示的是瞬时功率,即某个时刻做功的多少,例如第 \(\pu{5 s}\) 的功率;这里的 \(v\) 表示某时刻的速度,即瞬时速度;\(\theta\) 表示 \(F\) 和 \(v\) 的夹角。
一般情况下计算瞬时功率,求 \(v\) 时,可能需要利用牛二力学和运动学中的相关知识。
所以某时刻的功率,与此时做功的力 \(F\)、瞬时速度 \(v\) 和二者的夹角 \(\theta\) 有关。
例如:如图所示,一小球在从 \(A\) 端由静止移动到 \(B\) 端,问从 \(A\) 到 \(B\) 的过程中重力的功率 \(P_G\) 的变化。

分析:
当小球在 \(A\) 端时,\(v = 0\),所以起初 \(P_A = 0\);当小球在 \(B\) 端时,此时重力竖直向下,速度水平向左,二者夹角为直角,所以 \(\cos \theta = 0\),所以 \(P_B = 0\);当小球在从 \(A\) 到 \(B\) 中间某个点时,分析可知此时 \(P_G > 0\)。那么整个过程中 \(P_G\) 应该是先变大后变小。
汽车启动
额定(恒定)功率启动
相关概念:「额定功率」指发动机的最大功率。一般情况下,这里的「额定功率」对应的是牵引力的功率。
问题模型:一辆汽车在以水平面上,以额定功率从静止开始运动,汽车质量为 \(m\),运动过程中所受到的阻力 \(f\) 大小恒定,牵引力为 \(F\)。
运动状态分析:
首先对启动后的汽车进行受力分析:
同时根据 \(P = Fv\)(此时 \(\theta = 0\) 所以 \(\cos \theta = 1\))可得 \(F = \dfrac P v~ (2)\)。
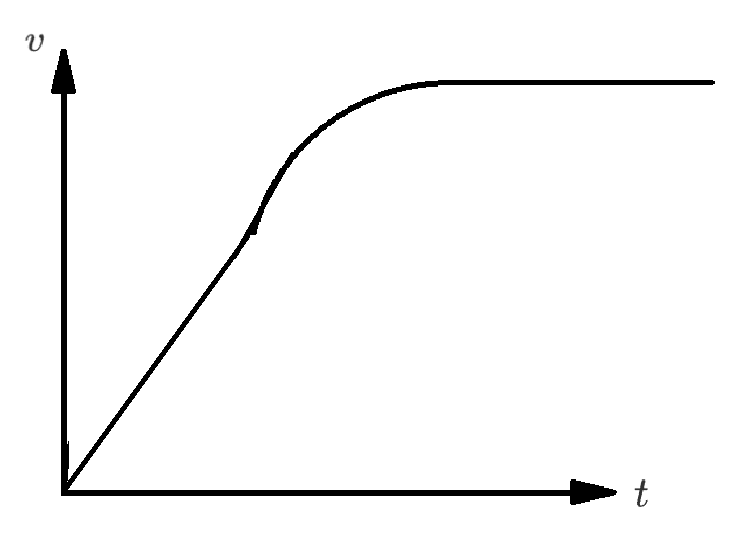
那么在最开始,由于物体从静止开始运动,所以物体有加速度 \(a\),因为 \(a,v\) 同向,所以 \(v\) 增大,由于 \(P\) 为额定功率始终不变,所以根据 \((2)\) 可知 \(F\) 减小,那么根据 \((1)\),由于 \(f\) 恒定,所以 \(a\) 减小,那么汽车做加速度减小的加速运动。
当 \(F\) 减小到与 \(f\) 相同时,\(a = 0\),所以物体速度不变,做匀速直线运动,其 \(v - t\) 图象如下。

解题思路:
- 找出研究对象。
- 找出题目条件对应的运动段。
- 画图,对该运动段的研究对象受力分析。
- 列出对应的受力分析式(平衡/牛二)。
注意:一般情况下,无论题目求的是哪个运动段,都要分析匀速运动阶段。
解题的语言描述:对「研究对象」的「某运动段」进行受力分析,如图(画出图像),列出「平衡式/牛二式」。
例:汽车发动机的额定功率为 \(\pu{60 kW}\),汽车质量为 \(\pu{5 t}\),运动中所受阻力的大小恒为车重的 \(0.1\) 倍。(\(\mathrm g\) 取 \(\pu{10m/s^2}\)),求:若汽车以额定功率启动,汽车所能达到的最大速度是多少?
分析:
涉及到「汽车所能到达的最大速度」,说明指的是汽车做匀速运动的运动段。
那么考虑对汽车的匀速运动阶段进行受力分析,如图所示。

则:
恒定加速度启动
问题模型:一辆汽车在以水平面上,以恒定加速度从静止开始运动,汽车质量为 \(m\),运动过程中所受到的阻力 \(f\) 大小恒定,牵引力为 \(F\)。
运动状态分析:
受力分析同「额定(恒定)功率启动」。
那么当 \(a\) 恒定时,根据 \((1)\) 和 \(f\) 始终不变,可得 \(F\) 保持不变。由于 \(a,v\) 同向,所以 \(v\) 增大,又根据 \((2)\),要使得 \(F\) 不变,则 \(P\) 增大,且 \(v,P\) 等比例增大。
当 \(P\) 达到汽车的最大功率时,由于受力不变,所以 \(a\) 仍保持不变,那么 \(v\) 仍然会增大;那么由于 \(P\) 不变,所以 \(F\) 减小。此时题目变成了 \(P\) 恒定,所以后续与「额定(恒定)功率启动」情况相同。
那么整个过程中的 \(v - t\) 图象如下:
\(P-t\) 图象如下:
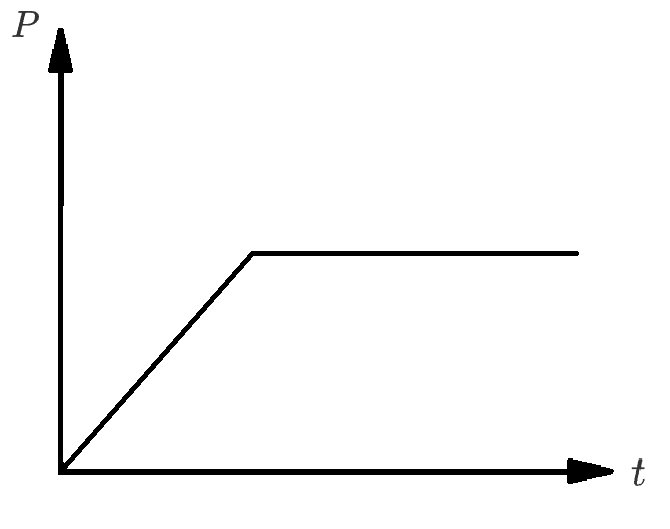
本质:起初 \(a\) 不变,后来 \(P\) 不变的运动。
解题思路:
一般要分析两个关键点:
- 匀加速直线运动变成加速度减小的加速度运动的点;
- 加速度减小的加速运动变成匀速直线运动的点(匀速直线运动阶段)。
解题的语言描述同「额定(恒定)功率启动」。
\(F - \dfrac 1 v\) 图象
解题思路:首先通过图象搞清楚汽车启动的类型是「恒定功率启动」还是「恒定加速度启动」。注意,由于横轴表示的是 \(\dfrac 1 v\) 而不是 \(v\),所以横轴从右向左,才表示 \(v\) 从 \(0\) 开始增大。那么当 \(v\) 从 \(0\) 开始增大时,若 \(F\) 起始阶段保持不变,则属于「恒定加速度」启动;反之,则属于「恒定功率」启动。然后考虑利用对应的启动类型来分析问题。
例:一辆汽车质量为 \(\pu{1E3 kg}\),最大功率为 \(\pu{2E4 W}\),在水平路面由静止开始做直线运动,最大速度为 \(v_2\),运动中汽车所受阻力恒定。发动机最大牵引力为 \(\pu{3E3 N}\),其行驶过程中牵引力 \(F\) 与车速的倒数 \(\dfrac 1 v\) 的关系如图所示,试求:
- \(v_2\) 的大小。
- 保持匀加速运动的时间是多少。

分析:
\(x\) 轴从右到左,\(v\) 从 \(0\) 开始逐渐增大,且初始阶段 \(F\) 保持不变,所以属于「恒定加速度启动」。那么首先考虑分析两个关键点的运动状态。
第一个关键点,即当汽车做匀速直线运动阶段,对应有 \(F = \pu{1E3 N}\) 且 \(\dfrac 1 v = \dfrac 1 {v_2}\) 考虑对汽车匀速阶段受力分析有:
第一个关键点,即当汽车匀加速运动到最大速度时,对应有 \(F = \pu{3E3 N}\) 且 \(\dfrac 1 v = \dfrac 1 {v_1}\),此时对汽车受力分析有:
同时根据 \(F = \dfrac P {v_1}\) 可知 \(v_1 = \dfrac{P}{F} = \dfrac {20000}{3000} = \pu{\dfrac{20}{3}m/s}\),所以匀加速运动的时间是 \(t = \dfrac{v_1}{a} = \pu{\dfrac{10}{3}s}\)。
动能定理
基础概念
动能
定义:一个物体因运动所具有的能量。
计算式:
单位:焦耳 \(\pu J\)。动能是标量。
动能定理
内容:
合外力做的功等于动能的变化量,即:
推导过程:
注意:在具体题目中,一般求 \(W_合\) 的方式为 $W_合 = W_1 + W_2 + W_3 + \cdots $,所以在代入每一个 \(W_i\) 时,无论它是正功还是负功,都直接代入,例如 \(W_1 = \pu{3 J},W_2 = \pu{-5 J},W_3 = \pu{1 J}\),则 \(W_合 = W_1 + W_2 + W_3 = 3 - 5 + 1 = \pu{-1 J}\)。
解题思路:
- 找出研究对象。
- 找到对应的运动段:一般涉及到两个关键点,即从哪到哪。
- 找到做功的力。
- 列出动能定理的式子。
解题的语言描述:对「研究对象」的「从 \(A\) 到 \(B\) 的运动段」列出对应 \(W_F\) 的动能定理式。
注意:一般情况下大题要运用动能定理时,最好写出 \(W_合 = \Delta E_k\)。
【模型】单段运动 - 圆周
基本知识
前置知识:
- 绳模型中运动到最高点时,其速度 \(v = \sqrt{\mathrm gr}\)。
- 杆模型中运动到最高点时,其速度 \(v = 0\)。
绳模型与杆模型的区别:绳子最高点无支撑,杆最高点有支撑。
重要技巧:
若题目告诉了某点的受力情况,则一定要通过受力分析将受力转换成速度,即
例题
例 1:如图所示,一绳长为 \(\pu{2.5 m}\) 细绳系着一质量为 \(\pu{4 kg}\) 的小球,若小球恰好在竖直平面内做圆周运动(\(\mathrm g\) 取 \(\pu{10m/s^2}\)),问:
- 小球通过最低点的速度是多少?
- 通过最低点的拉力是多少?
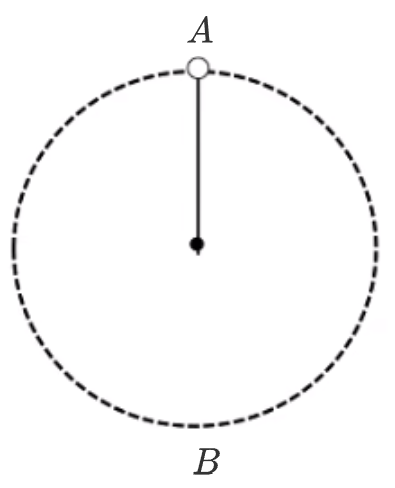
分析:
对于第一问,考虑小球从 \(A\to B\) 的运动段,做功的力是重力,那么根据 \(W_合 = \Delta E_k\) 有:
对于第二问,考虑对最低点的小球受力分析 ,则有
注意:对于第一问 \(h = 2L\) 而不是 \(h = L\)。
例 2:如图所示,竖直平面内一半径为 \(R\) 的半圆形轨道,两边端点等高,一个质量为 \(m\) 的质点从左端点由静止开始下滑,滑到最低点时对轨道压力为 \(2m \mathrm g\),\(\mathrm g\) 为重力加速度,则此下滑过程克服摩擦力做的功是多少?
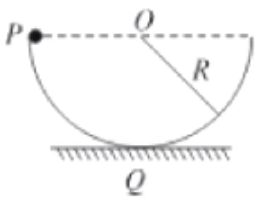
分析:
此题目告诉了小球滑到最低点时的相关受力,所以考虑通过受力转化为速度。
那么首先考虑对最低点的小球受力分析有
题目求的是「下滑过程中克服摩擦力做的功」,发现此时摩擦力方向不断改变,且根据 \(f = \mu F_N\),\(F_N\) 不确定,所以 \(f\) 也不确定,所以不能直接利用功的计算式或定义来求解。考虑动能定理。
那么对小球从 \(P \to Q\) 的运动段分析,此时做功的力为重力 \(G\) 和摩擦力 \(f\),那么根据动能定理 \(W_合 = \Delta E_k\) 有:
所以摩擦力做的功是 \(- \dfrac 1 2 m \mathrm g R\),那么克服摩擦力做的功是 \(\dfrac 1 2 m \mathrm g R\)。
例 3:美国的 NBA 篮球赛非常精彩,吸引了众多观众,经常能看到这样的场面:在终场前 \(\pu{0.1 s}\) 的时候,运动员把球投出且准确命中,获得比赛的最后胜利,已知球的质量为 \(m\),运动员将篮球投出,球出手时的高度为 \(h_1\),动能为 \(E_k\),篮筐距地面高度为 \(h_2\)。不计空气阻力。则篮球进框时的动能是多少?
分析:
对篮球从投出到进框的运动段分析,此时做功的力为重力 \(G\),根据动能定理 \(W_合 = \Delta E_k\) 有
注意:这里的 \(G\) 做负功,而非正功,所以 \(W_G = - m \mathrm g (h_2 - h_1)\)。
例 4:某人在高 \(h\) 处抛出一个质量为 \(m\) 的物体,不计空气阻力,物体落地时速度为 \(v\),该人对物体所做的功为多少。
分析:
对物体从抛出到落地的运动段分析,此时做功的力有人对物体的作用力 \(F_人\) 和重力 \(G\),根据动能定理 \(W_合 = \Delta E_k\) 有
总结:利用动能定理解决问题时,对于 \(W_合\),有时候不一定要找出所有做功的具体的力,例如本题中将「人对物体的作用力」作为做功的力之一,但是并不清楚人对物体做了几个力,或者其力的性质是什么。同时,题目求「人对物体所做的功」也暗示了要将人对物体的作用力整体作为做功的力来看待。
【模型】多段运动 - 直线
基本知识
【解题关键点】如何选取初末状态。
【问题类型】
- 求某点的物理量:一般选用该点对应状态为其中一个状态(初/末状态),再选用另一个速度已知的点为另一状态(末/初状态)。
- 求某一段的物理量:选用两个速度已知的点为初末状态。
例题
例 1:民用航空客机的紧急出口打开时,会自动生成一个由气囊构成的斜面,模型简化如图所示。光滑斜面的竖直高度 \(AB = \pu{3.2 m}\),斜面长 \(AC = \pu{4.0 m}\),斜面与水平地面 \(CD\) 段间有一段小圆弧平滑连接。当物体由静止开始滑下,其与地面间的动摩擦因数均为 \(\mu = 0.5\),不计空气阻力,\(\mathrm g = \pu{10 m/s^2}\),求:
- 人滑到斜面底端 \(C\) 时的速度大小。
- 人离开 \(C\) 点后还要在地面上滑行多远才能停下。

分析:
对于第一问,由于求的是 \(C\) 点的速度,同时 \(A\) 点静止(说明速度为 \(0\)),则考虑对人从 \(A \to C\) 的运动段分析,此时做功的力为重力 \(G\),根据动能定理 \(W_合 = \Delta E_k\) 有
对于第二问,求的是从 \(C\) 点到停下这一段的距离,发现 \(v_C\) 和 \(v_D\) 已知,所以考虑对人从 \(C \to D\) 的运动段分析,此时只有滑动摩擦力 \(f\) 做功,根据动能定理 \(W_G = \Delta E_k\) 有
注意:这里的 \(W_f\) 做负功,而不是正功。
另解:
对于第二问,若选取 \(A \to D\) 的运动段分析,则此时做功的力为重力 \(G\) 和滑动摩擦力 \(f\),则有
\[W_G + W_f = 0 \implies m \mathrm g h = \mu m \mathrm g x \implies x = \dfrac h \mu = \pu{6.4 m} \]所以选用不同的初末状态对应的力的做功不同,计算量也不同。应该在平时做题中多体会选择合适初末状态的技巧,从而加快计算速度。
一般情况下,只要选取的初末状态包含在题目涉及的运动段当中,基本都是可解的。
例 2:如图所示,一粗糙斜面 \(AB\) 于光滑圆弧轨道 \(BCD\) 相切,\(O\) 为圆弧轨道的圆心,\(OD\) 处在同一水平面上,\(C\) 为圆弧轨道的最低点,圆弧 \(BC\) 所对圆周角 \(\theta = 37^\circ\)。已知斜面 \(AB\) 的长度为 \(L = \pu{2.0 m}\),圆弧轨道半径为 \(R = \pu{0.5 m}\),质量为 \(m = \pu{1 kg}\) 的小物块(可视为质点)从斜面顶端 \(A\) 点处由静止开始沿斜面下滑,从 \(B\) 点进入圆弧轨道运动并从轨道边缘 \(D\) 点竖直向上飞出,离开 \(D\) 点以后上升的最大高度为 \(h = \pu{0.4 m}\),\(\sin 37^\circ = 0.6\),\(\cos 37^\circ = 0.8\),重力加速度 \(\mathrm g = \pu{10 m/s^2}\),空气阻力不计,求:
- 物块第一次经 \(C\) 点时对圆弧轨道的压力。
- 物块第一次返回斜面运动的最高点距 \(A\) 点的距离。

分析:
首先对于第一问,由于求的是「\(C\) 点的物理量」,所以选择 \(C\) 点作为一个状态点。此时 \(A\) 点速度已知,但由于从 \(A \to C\) 的运动段中,有重力 \(G\) 和滑动摩擦力 \(f\) 做功,但是由于此时粗糙面 \(\mu\) 未知,所以 \(W_f\) 无法求出,且此时 \(C\) 点速度未知,所以不能选取 \(A\) 点作为另一个状态点。
设物体从 \(D\) 点竖直向上飞出后,当其运动到 \(E\) 点时速度为 \(0\),且 \(C \to E\) 只有重力做功。那么考虑对 \(C \to E\) 运动段分析,则根据 \(W_合 = \Delta E_k\) 有
那么在 \(C\) 点有:
对于第二问,第一次返回斜面运动的最高点为 \(F\)。考虑选取从 \(C \to F\) 的运动段分析,这个过程中滑动摩擦力 \(f\) 和重力 \(G\) 做功。此时依然不知道 \(\mu\),所以考虑求出 \(\mu\)。
此时 \(A\) 点和 \(E\) 点的速度已知,都为 \(0\),考虑对 \(A \to E\) 的运动段分析,此时滑动摩擦力 \(f\) 和重力 \(G\) 做功,那么根据动能定理 \(W_合 = \Delta E_k\) 有
那么再选取从 \(C \to F\) 的运动段分析,根据动能定理有:
所以最高点距离 \(A\) 的距离为 \(2 - 1 = \pu{1 m}\)。
总结:对于解题过程中发现未知的物理量,要善于利用合适的运动段分析,通过动能定理求出该物理量,然后求解,例如本体中的 \(\mu\)。
【模型】往返运动
问题模型:如图所示,粗糙的斜面 \(AB\) 下端与光滑的圆弧轨道 \(BCD\) 相切于 \(B\),整个装置竖直放置,\(C\) 是最低点,圆心角 \(\angle BOC = \theta = 37^\circ\),\(D\) 与圆心 \(O\) 登高,圆弧轨道半径 \(R = \pu{1.0 m}\),斜面长 \(L = \pu{4.0 m}\),现有一个质量 \(m = \pu{1.0 kg}\) 的小物体 \(P\) 从斜面 \(AB\) 上端 \(A\) 点无初速度下滑,物体 \(P\) 与斜面 \(AB\) 之间的动摩擦因数为 \(\mu = 0.25\),\(\mathrm g\) 取 \(\pu{10 m/s^2}\),求:
- 物体 \(P\) 从空中又返回到圆轨道和斜面,做往复运动,在整个过程中,物体 \(P\) 对轨道上 \(C\) 点的最小压力是多大?
- 物体 \(P\) 从空中又返回到圆轨道和斜面,做往复运动,在整个过程中,物体在 \(AB\) 上运动的路程是多少?

求解思路:
对于第一问,首先发现,当物体运动到 \(E\) 折返回到斜面 \(AB\) 上时,由于摩擦力做功,机械能会转化为热能,所以每次折返回到粗糙斜面 \(AB\) 时,能到达的最高高度会越来越小,设每次到达的最高点为 \(F\)。同时根据题意可知 \(\mu < \tan \theta\),所以物体到达 \(AB\) 斜面后,不会静止在 \(AB\) 面上。考虑对 \(C \to F\) 的运动段分析,根据动能定理有 \(- m \mathrm g h - fs = 0 - \dfrac 1 2 m{v_C}^2\),那么此时 \(h\) 和 \(s\) 均减小,所以 \(v_C\) 减小。
设圆弧轨道 \(C\) 点右侧与 \(B\) 点等高处为 \(B'\) 点。那么当下降的高度逐渐减小,直至 \(F\) 点与 \(C\) 点重合时,考虑对物体从 \(B \to C\) 的运动段分析,此时只有重力做功,所以物体会始终会在圆弧 \(BB'\) 上一直做往返运动,那么此时 \(C\) 点的速度就是最小速度。则根据动能定理有
对 \(C\) 点受力分析有:
那么此时 \(C\) 点所受的压力也最小,所以物体 \(P\) 对轨道上 \(C\) 点的最小压力为 \(\pu{14 N}\)。
对于第二问,可以发现物体在斜面 \(AB\) 上做往返运动时,摩擦力只有方向改变,而大小不变,而对于方向改变大小不变的力做功,我们的计算方式是 \(W_f = fs \cos \theta\),此时 \(\theta = 0\),所以可以考虑利用 \(W_f = fs\) 将物体在 \(AB\) 上运动的路程求出。
根据上述的分析过程可知,物体的运动是从 \(A\) 点以初速度为 \(0\) 开始运动到 \(E\) 点,然后再返回 \(AB\) 斜面不断往返运动,当物体运动的最高点 \(F\) 与 \(B\) 点重合时,物体在斜面上不再做功。所以整个过程中,摩擦力做功的运动段是从 \(A\) 点进行若干次往返运动后回到 \(B\) 点的运动段。此时初状态速度为 \(0\),末状态速度也为 \(0\)。那么考虑对这一运动段分析,有重力和摩擦力做功,根据动能定理有
总结:
对于第一问,有三个关键点:
- 往返运动物体为什么不会返回 \(A\) 点:涉及到一部分能量和机械能守恒的知识,这里简单来讲就是摩擦做功生热,会导致机械能转化为热能,从而使得机械能整体逐渐减小,导致往返运动在斜面上不会返回 \(A\) 点(速度为 \(0\) 的点始终低于 \(A\))。
- 做往返运动的过程中为什么物体不会静止在某个地方不动:在斜面 \(AB\) 的最高点,始终有 \(\mu < \tan \theta\),根据牛二力学的相关知识可知,物体势必一定会滑下;在圆弧轨道上,物体始终受重力 \(G\),受力不平衡。
- 建立「最小压力」和「最小速度」的关系:题目求最小压力,考虑到对 \(C\) 受力分析,那么根据 \(m \dfrac{{v_C}^2}{R} = F_N - m \mathrm g\) 将最小压力转化为最小速度,再根据动能定理将最小速度转化为「往返运动时能够运动到的最高点的最低位置(也就是此题的 \(B\) 点)」。
对于第二问,有一个关键点:题目求的是路程,那就考虑学过的与路程有关的定义式/计算式,发现只有在「变力做功计算」中学过的方向改变,大小不改变的力的做功,结合此题,这里方向改变大小不改变的力即为摩擦力,那么考虑根据 \(W_f = fs \cos \theta\) 求解。
根据这道题可以总结出有关往复运动的一些技巧:
- 题目求某点的某物理量的最值,可以通过受力分析转化为其它物理量的最值,再根据动能定理求出对应的最值。
- 求解往复运动问题的关键点在于「分析运动过程」,借助机械能守恒和能量相关的知识可以更好的分析出运动过程。
【模型】链条(无法看成质点)的动能定理
解题方法
- 画出初 - 末状态图。
- 对比图象找出变化部分的物体:一般情况下可看作物体(链条)的某一段运动,而不是整体运动。
- 找出变化部分的质心变化列动能定理:相当于将变化部分物体看成质点,转化为传统的动能定理求解。
例题
例 1:质量为 \(m\) 的均匀链条长为 \(L\),开始放在光滑的水平桌面上时,有 \(\dfrac 1 4\) 的长度悬再桌边缘,如图所示。松手后,链条滑离桌面,问:从开始到链条滑离桌面过程中重力做了多少功?

分析:
初末状态原题中已经画出。对比初末状态图象,可以发现相当于初始状态水平的 \(\dfrac 3 4 L\) 的链条,运动到末状态下方的 \(\dfrac 3 4 L\) 链条,变化部分的质心恰好为对应这两部分链条的几何中心,如图所示:
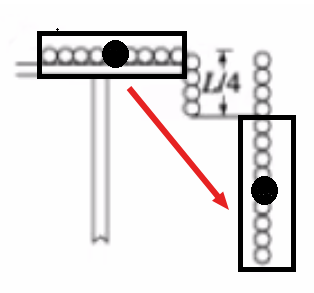
那么此时变化部分的质心下降的高度为 \(h = \dfrac 1 4 L + \dfrac 1 4 L \times \dfrac 1 2 = \dfrac 5 8 L\)。那么整个过程重力做功为:
例 2:如图所示,质量为 \(m\) 的均匀链条长为 \(L\),水平面光滑,\(\dfrac L 2\) 垂在桌面下,将链条由静止释放,设桌面的高度大于 \(L\),则链条全部滑离桌面时()
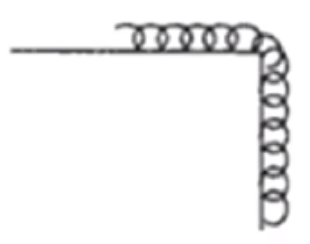
A. 其动能为 \(\dfrac 1 2 m \mathrm g L\)
B. 其速度为 \(\dfrac{\sqrt{3\mathrm g L}}{2}\)
C. 其速度为 \(\dfrac{\sqrt{5 \mathrm g L}}{2}\)
D. 重力做功为 \(\dfrac 3 8 m \mathrm g L\)
分析:
同理上题可知,变化部分物体质心竖直位移为 \(h = \dfrac L 2 + \dfrac L 4 = \dfrac 3 4 L\),此时
那么根据动能定理可知
故选 BD。
注意:求链条重力所做的功时,相当于只有 \(\dfrac 1 2\) 的链条做功,所以这里代入的 \(G\) 是 \(\dfrac 1 2 m \mathrm g\);而利用动能定理求链条的速度时,涉及的是整个链条的速度和动能,所以代入 \(\dfrac 1 2 m v^2\) 中的 \(m\) 是整个链条的质量。
摩擦力做功的特点
直线运动
基本知识
前提:① 不受外力;② 直线运动。
特点:斜面摩擦力 \(\times\) 斜面距离 \(=\) 水平面摩擦力 \(\times\) 水平面距离。

如图所示,那么有:
其中,\(\mu m \mathrm g \cos \theta\) 是斜面摩擦力,\(a\) 是斜面距离,\(\mu m \mathrm g\) 是水平(地面受到的)摩擦力,\(b\) 是水平距离。
例题
例 1:如图所示,一木块沿着高度相同、倾角不同的三个斜面由顶端静止滑下,若木块和各斜面间的动摩擦因数相同,则滑到底端时的动能大小关系是什么。

分析:
根据 \(W_合 = m \mathrm g h + W_f = \dfrac 1 2 m v^2\),由于三个斜面的高度相同,所以 \(m \mathrm g h\) 相同,那么只需要比较 \(W_f\)。
根据直线运动中摩擦力做功的特点可知 \(W_f = \mu m \mathrm g s\),其中 \(s\) 表示水平面距离。因为 \(AB < AC < AD\),所以倾角越大,\(W_f\) 越大,则动能越大。
例 2:如图所示,\(OD\) 是水平面,\(AB\) 是斜面,初速度为 \(v_0\) 的物体从 \(D\) 点出点除法沿 \(DBA\) 滑动到顶点 \(A\) 时速度刚好为零。如果斜面改为 \(AC\),让该物体从 \(D\) 点出发沿 \(DCA\) 滑动到 \(A\) 点且速度刚好为零,则物体具有的初速度和 \(v_0\) 的大小关系如何?(已知物体与接触面之间的动摩擦因数处处相同且不为零)

分析:
设物体沿 \(DBA\) 运动摩擦力做的功为 \(W_f\),沿 \(DCA\) 运动初速度为 \({v_0}'\),摩擦力做的功为 \({W_f}'\)。则对两次运动利用动能定理分析有:
那么对于物体沿 \(DBA\) 的运动,摩擦力做的功等于 \(AB\) 段摩擦力做的功加上 \(BD\) 段摩擦力做的功,即
同理,物体沿 \(DCA\) 运动,摩擦力做的功等于 \(AC\) 段摩擦力做的功加上 \(CD\) 段摩擦力做的功,即
所以 \(W_f = {W_f}'\)。
总结:要善于将斜面上摩擦力做功转化为水平面上摩擦力做功求解。
曲线运动
基本知识
特点:
- 对于不同运动轨迹,滑动摩擦力 \(\mu F_N\) 中 \(F_N\) 的大小与运动的曲面有关:是凹面还是凸面(体现在下方例 1)。
- 对于同一运动轨迹,\(F_N\) 的大小与速度大小 \(v\) 有关:可以对轨迹上一点进行受力分析求出二者关系(体现在下方例 2)
例题
例 1:如图所示,上凸桥 \(ABC\) 和凹桥 \(A'B'C'\) 由相同材料制成,轨道半径和粗糙程度相同,有一小物体前后两次以相同的初速度经两桥面到 \(C\) 和 \(C'\),若路程相同,则到达 \(C\) 的速度 \(v\) 和到达 \(C'\) 的速度 \(v'\) 的大小关系如何?
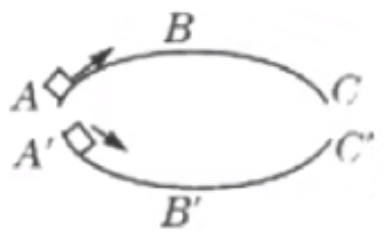
分析:
对于上凸桥和凹桥的两个运动段,根据动能定理有
由于两段运动 \(h,\mu,s\) 均相同,所以只需要比较 \(F_N\) 和 \({F_N}'\) 的大小关系。
那么对于上凸桥有 \(F_合 = m \mathrm g - F_N\),对于下凹桥有 \(F_合 = {F_N}’ - m \mathrm g\),所以 \({F_N}' > m \mathrm g > F_N\),所以 \(v > v'\)。
例 2:如图所示,一物块以 \(\pu{3 m/s}\) 的初速度从曲面 \(A\) 点下滑,运动到 \(B\) 点速度仍为 \(\pu{3 m/s}\)。若物体以 \(\pu{2 m/s}\) 的初速度仍由 \(A\) 点下滑,则它运动到 \(B\) 点时的速度与 \(\pu{2 m/s}\) 的大小关系如何。
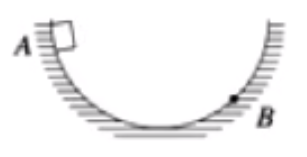
分析:
首先对物体从 \(A \to B\) 的运动段分析,此时重力 \(G\) 和滑动摩擦力 \(f\) 做功,根据动能定理有
当初速度 \(v_A = \pu{3 m/s}\) 时,根据题意可知 \(v_B = v_A\),所以 \(W_合 = m \mathrm g h + W_f = 0\)。
由于\(m \mathrm g h\) 始终保持不变,摩擦力做功 \(W_f = \mu F_N s\),\(\mu,s\) 由于是同一轨道所以不便。那么需要判断 \(v_A\) 变为 \(\pu{2 m/s}\) 后对 \(F_N\) 的大小影响。
对 \(A \to B\) 轨道上任意一点进行受力分析如下图所示:

那么有
由于 \(v_A\) 增大,所以 \(F_N\) 增大,又由于 \(W_f\) 是负功,所以摩擦力做的负功更少,所以 \(v_B> v_A\)。即到达 \(B\) 点时的速度 \(v_B > \pu{2m/s}\)。(若做功相较于 \(v_A = \pu{3 m/s}\) 不变,则 \(W_合 = 0\),由于现在做的负功更少,所以 \(W_合 > 0\),那么 \(v_B > v_A\))
能量
基础介绍
动能:由于物体运动所具有的能量。
内能:可以通俗的理解为物体因为发热所具有的能量(发热量)。
势能:物体具有「潜在的(potential)能量」,或者可以理解为「对外做功的能力」,与物体所在空间位置有关。
学习能量的两大目的:
- 应用到动能定理中,一般情况下求对应的能量可以转化为力做的功。
- 弄清楚什么力做功会改变这个能量。
重力势能
定义
重力势能用 \(E_{PG}\) 表示,单位为焦耳 \(\pu J\)。其定义式为
其中,\(h\) 表示物体距离 "\(0\)" 势能面的高度,若物体比零势能面高,则 \(h > 0\);反之,\(h < 0\)。那么 \(h\) 是标量,则其大小直接与数轴上点的位置相关,数轴上左边的点比右边的点小。
注意:若题目没有说明,则默认地面为 \(0\) 势能面;若题目已经说明,则选用题目给定的 \(0\) 势能面。有些大题可以自己选用 \(0\) 势能面,一般情况下选用题目中最低的平面作为 \(0\) 势能面,目的是保证所有的重力势能都为正,方便计算。
特征
物体的重力势能 \(E_{PG}\) 与 \(0\) 势能面的选取有关;但重力势能的变化量 \(\Delta E_{PG}\) 与 \(0\) 势能面的选取无关。
注意:题目中「势能的变化量」是末状态势能 \(-\) 初状态势能,有可能为负。若题目直接求「势能的减少量」,此时一般都是大势能 \(-\) 小势能,一般都为正。
重力势能与功的关系
重力势能反应的是物体对外做功的能力,物体所具有的重力势能越大,其做功的本领就越强。有
即重力做的功等于负的重力势能的变化量。所以重力做功会改变重力势能,具体来说:重力做正功 \(\to\) 能量减少;重力做正功 \(\to\) 能量增多。
一般通过此式将求重力势能的问题转化为求重力做的功。
弹性势能
定义
弹簧由于形变所具有的能量,一般用 \(E_{P~弹}\) 表示,单位是焦耳 \(\pu J\)。其定义式为
该表达式不需要记忆。
所以弹性势能与劲度系数 \(k\) 和形变量 \(\Delta x\) 有关。对于同一根弹簧:
- 形变量越大,弹性势能越大。
- 形变量越小,弹性势能越小。
注意:形变既不是长度,也不是位移,
弹性势能与功的关系
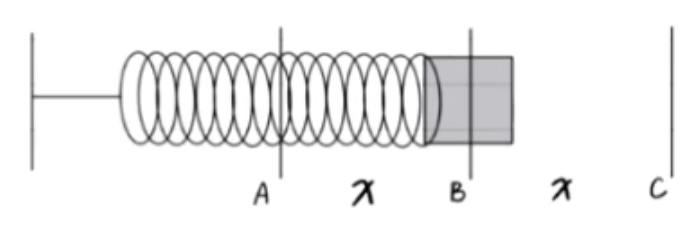
如图所示,物体固定在弹簧的一端移动,当物体活动端位于 \(B\) 时恰好处于原长。则:
- 当弹簧从 \(B \to A\) 移动,由于弹力水平向右,位移水平向左,所以弹力做负功,形变量变大(从无到有),弹性势能增大。
- 当弹簧从 \(B \to C\) 移动,由于弹力水平向左,位移水平向右,所以弹力做负功,形变量变大(从无到有),弹性势能增大。
- 当物体从 \(A \to B\) 运动,由于弹力水平向右,位移水平向右,所以弹力做正功,形变量变小(从有到无),弹性势能减小。
- 当物体从 \(A \to C\) 运动,从 \(A \to B\) 做负功,从 \(B \to C\) 做正功,且 \(B\) 点恰好处于原长,\(AB = BC = x\),所以弹力做功总体为 \(0\)。
结论:
弹簧弹力做功,会改变弹性势能:
- 弹力做正功,弹性势能减小。
- 弹力做负功,弹性势能增大。
- 弹簧弹力做功 \(W_N = - \Delta E_{P~弹}\),即弹力做功的正负与弹性势能增大/减小呈反向关系。一般通过此式将求弹性势能的问题转化为求弹力做的功。
同理重力势能,弹性势能的变化量 \(\Delta E_{P~弹}\) 是末状态弹性势能 \(-\) 初状态弹性势能。所以弹力做功等于负的弹性势能的变化量。
注意:对于所有的势能,都有对应力做功等于负的对应势能的变化量。
内能(热能)
定义
内能用发热量 \(Q\) 表示,定义为负的一对滑动摩擦力做的总功。
对于定义的理解:
- 首先必须是滑动摩擦力,而不是静摩擦力。
- 然后是一对滑动摩擦力做的总功:一般情况下一对滑动摩擦力作用在两个物体上,假设是 \(A,B\),则这里的总功即为 \(A\) 对 \(B\) 的摩擦力做的功加上 \(B\) 对 \(A\) 的摩擦力做的功,即 \(W_合 = W_{A \to B} + W_{B \to A}\)。
那么有
这里的 \(\Delta s\) 指的是两物体 \(A,B\) 相对运动的路程。
由于一对滑动摩擦力做的总功是负的(前面常见力做功的正负涉及过),那么放热量一定是正的。
注意:摩擦力做负功则放热,但是摩擦力做正功并不是吸热。
总结:
- 重力做功等于负的重力势能变化量。
- 弹力做功等于负的弹性势能变化量。
- 发热量(内能)等于负的一对摩擦力做的总功。
机械能守恒
机械能
定义
机械能是势能和动能的总和。
注意:势能中只包含重力势能和弹性势能,不包含电势能。
表达式:
不同情况下的机械能
单个物体:
单个物体 + 弹簧的系统:
多个物体:
机械能守恒的条件
本质
势能与动能的互相转化。
不同情况下机械能守恒的条件
单个物体:
即重力势能与动能的相互转化。例如:当一个物体重力做了 \(\pu{10 J}\) 的功,根据 \(W_G = - \Delta E_{PG}\) 可知重力势能减小了 \(\pu{10 J}\),此时只有重力做功,那么 \(W_合 = W_G = \Delta E_k\),所以动能增大了 \(\pu{10 J}\)。根据 \(W_机 = E_{PG} + E_k\) 可知机械能守恒。
所以除了重力之外做的功整体为 \(0\) 时机械能守恒,即重力做功不改变机械能,除了重力之外的力做功才会改变机械能。
注意:只有重力做功机械能守恒这句话并不准确。比如涉及到三个力重力 \(G\),摩擦力 \(f\) 以及合外力 \(F\) 做功时,假设 \(W_G = \pu{10 J},W_f = \pu{-5 J},W_F = \pu{5 J}\),那么此时并非只有做功,但可以分析得到机械能守恒。
单个物体 + 弹簧的系统:除了重力和系统的内力以外做的功为 \(0\) 时机械能守恒。
多个物体:除了系统内各个重力,和系统内各个物体的相互作用力做功以外做的功为 \(0\) 时机械能守恒。
机械能与做功的关系
除重力 \(G\) 以外的力做功 \(=\) 机械能的变化量。
- 除重力外其它力做正功,则机械能增大。
- 除重力外其它力做负功,则机械能减小。
总结:重力势能、弹性势能和内能与对应力做功(重力、弹力和摩擦力做功)的变化负相关,即做多少功,能量就减小多少;动能和机械能与其对应力(合外力、除重力 \(G\) 之外其它的力)做功呈正相关,即做多少功,能量就增加多少。
机械能守恒的判断
一般情况下,此类题都是针对「单个物体」的情况,所以这里只以单个物体为例。
判断方法:
- 看除了重力是否还有其它力做功,或其它力做功之和是否为 \(0\) 来判断。例如除了重力还有摩擦力做功,则机械能不守恒。
- 根据 \(E_机 = E_{PG} + E_k\),分别考虑 \(E_{PG}\) 和 \(E_k\) 的变化判断。例如 \(E_k = 0\),\(E_{PG}\) 不断变化,则机械能不守恒。
例:在下列情况下机械能守恒的有()
A. 在空气中匀速下落的降落伞
B. 在竖直面做匀速圆周运动的物体
C. 做自由落体运动的物体
D. 沿斜面匀速下滑的物体
分析:
对于选项 A:降落伞受力分析可知除了重力做功还有空气阻力做功,除重力外做功不为 \(0\),所以机械能不守恒;或者考虑到 \(E_{机} = E_{PG} + E_k\),由于物体匀速下滑(速度不变),所以 \(E_k = 0\),物体下落, 所以 \(E_{PG}\) 减小,所以机械能减小。
对于选项 B:由于做匀速圆周运动,所以速度不变,所以动能不变;而物体在竖直平面内做匀速圆周运动,说明重力势能在改变,所以根据 \(E_机 = E_{PG} + E_k\) 可知机械能不守恒。
对于选项 C:做自由落体运动的物体只有重力做功,所以机械能守恒。
对于选项 D:由 AB 分析同理,动能不变,重力势能减小,所以机械能减小。
功能关系转化
知识总结
负相关功能关系:
- 重力势能:\(W_G =- \Delta E_{PG} = -(E_{PG~末} - E_{PG~初})\)。
- 弹性势能:\(W_G = - \Delta E_{P~弹} = - (E_{P~弹末} - E_{P~弹初})\)。
正相关功能关系:
- 动能:\(W_合 = \Delta E_k = E_{k~末} - E_{k~初}\)。
- 机械能:\(W_{除~G} = \Delta E_机\)。
特殊:内能:\(Q =\) 负的一对摩擦力做功之和。
关键:要利用动能定理 \(W_合 = \Delta E_k\) 把除了动能之外的其它能量都转化为功。
例题
例 1(弹簧 - 动能定理):如图所示,光滑水平面 \(AB\) 与竖直面内光滑的半圆形导轨在 \(B\) 点衔接,导轨半径为 \(R\),一个质量为 \(m\) 的静止物块在 \(A\) 处压缩弹簧,释放物块后再弹力作用下获得一向右速度,当它经过 \(B\) 点进入导轨达到最高点 \(C\) 时,对轨道的弹力大小恰好等于其重力,已知重力加速度为 \(\mathrm g\),求释放物体前弹簧储存了多大的弹性势能?

分析:
由于题目告诉了 \(C\) 点的受力情况(对轨道的弹力大小恰好等于其重力),那么考虑对 \(C\) 点的物块受力分析有
题目求弹性势能,考虑将其转化为弹力做功。考虑对物块选取从 \(A \to C\) 的运动段分析,此时重力 \(G\) 和弹力做功,那么有
由于当物块处于 \(C\) 点时,弹簧为原厂,所以 \(E_{P~弹末} = 0\),那么根据 \(W_弹 = - \Delta E_{P~弹}\) 可得 \(E_{P~弹初} = W_弹 = 3 m \mathrm g R\)。
所以释放物块前弹簧储存了 \(3 m \mathrm g R\) 的弹性势能。
例 2(机械能 - 动能定理):一个小球从空中的 \(a\) 点运动到 \(b\) 点的过程中,重力做功 \(\pu{5 J}\),除重力之外其它力做功 \(\pu{2 J}\),则小球()
A. 在 \(a\) 点的重力势能比在 \(b\) 点少 \(\pu{5 J}\)
B. 在 \(a\) 点的动能比在 \(b\) 点多 \(\pu{7 J}\)
C. 在 \(a\) 点的机械能比在 \(b\) 点少 \(\pu{2 J}\)
D. 在 \(a\) 点的机械能比在 \(b\) 点多 \(\pu{2 J}\)
分析:
首先对小球从 \(a\) 点到 \(b\) 点的运动段分析,那么根据动能定理有
那么由于重力做功 \(\pu{5 J}\),所以重力势能减小 \(\pu{5 J}\),所以 \(a\) 点重力势能比 \(b\) 点多 \(\pu{5 J}\);合外力做功 \(\pu{7 J}\),所以动能增大 \(\pu{5 J}\),所以 \(a\) 点动能比 \(b\) 点少 \(\pu{7 J}\);除了重力其它力做功 \(\pu{2 J}\),所以机械能增大 \(\pu{2 J}\),所以 \(a\) 点机械能比 \(b\) 点少 \(\pu{2 J}\)。
多物体题型
多物体机械能守恒
相关知识&技巧
使用前提:无外部干扰,系统自发运动,如:释放小球,小球下落。
适用范围:符合旋转杆模型或不用分解速度的绳模型。
规定:选取整个运动中达到的最低点为零势能面。
列式(以下三个缺一不可):
-
能量守恒定律表达式:
\[E_初 = E_末 \]即初始能量等于最终能量。
-
关联速度表达式(两个物体速度之间的关系):
若是旋转关联:
\[v = r \omega \]即单个物体中的所有点角速度 \(\omega\) 相同(在曲线运动中涉及过)。
若是绳、杆关联:① 找到实际运动(合运动);② 绳、杆方向建系分解合运动;③ 根据沿绳、杆速度大小相等列等式。(同样在曲线运动涉及过)
-
若题目涉及单个物体的物理量,则可能需要列单个物体的动能表达式:
\[W_1 + W_2 + W_3 + \cdots + \Delta E_k \]
解题步骤:
- 选取零势能面。
- 列出能量守恒定律表达式。
- 列出关联速度定律表达式。
- (选)若涉及单个物体物理量,列出单个物体动能表达式。
- (选)若题目涉及具体的力,考虑对单个物体进行受力分析求解。
- 计算:注意一般情况下此类题目给定的数据都较为复杂,所以大部分情况下答案都是带根号的,所以若计算得到没有带根的答案则需要检查。
基础题型示例
长为 \(L\) 的轻杆两端分别固定有质量为 \(m\) 的小铁球,杆的三等分点 \(O\) 处有光滑的水平转动轴。用手将该装置固定在杆恰好水平的位置,然后由静止释放,当杆到达竖直位置时:
- 求 \(1\) 和 \(2\) 的速度是多少?
- 轻杆对 \(1\) 和 \(2\) 做的功分别是多少?
- 此时杆对 \(2\) 的力是多少?
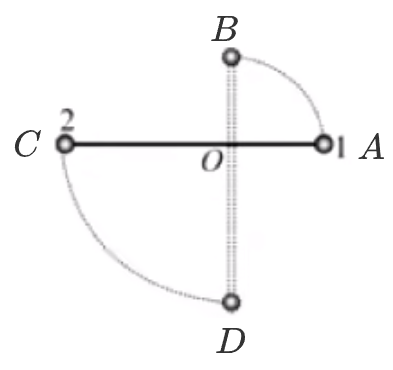
分析:
对于第一问:
首先选取 \(D\) 点所在平面为零势能面。
然后列出能量守恒定律表达式如下:
注意:
- 这里 \(E_初\) 和 \(E_末\) 都较为复杂,所以最好按照先考虑每个物体的重力势能,再考虑每个物体动能的顺序列式,保证不重不漏。
- 这里代入各个物体的质量和速度时,最好代入 \(m_1,m_2,v_1,v_2\) 而非 \(m,v\),这是为了防止后续计算出错。
然后再列出关联速度表达式,此时 \(1\) 和 \(2\) 都是同一个绕中心旋转的杆上的点,所以 \(\omega_1 = \omega_2\),那么根据 \(v = r \omega\) 可知 \(v_1 = \dfrac 1 2 v_2\)。将其代入上述能量守恒表达式得:
那么根据 \(v_1 = \dfrac 1 2 v_2\) 可得 \(v_1 = \sqrt{\dfrac 2 {15}\mathrm g L}\)。
注意:这里得到的 \(v_2\) 带根的结果不需要化简。
对于第二问:
题目问的是杆对物体做的功,属于单个物体的物理量,那么考虑列出单个物体的动能表达式。
那么先对 \(1\) 物体从 \(A \to B\) 运动段分析,此时做功的力为重力 \(G\),且不知道杆是否对 \(1\) 做功,那么假设杆做功了,根据动能定理有:
同理,对 \(2\) 物体从 \(C \to D\) 运动段分析,此时做功的力为重力 \(G\),且不知道杆是否对 \(2\) 做功,假设做功,则根据动能定理有:
总结:
- 当不知道某个力是否做功时,可以先假设其做功,然后列式计算求得该力做的功,如果求得功为 \(0\),则说明 没有做功,反之则做功。
- 观察发现,杆对 \(1\) 和 \(2\) 的做功之和恰好为 \(0\),此时对于整个系统而言,只有重力做功,这验证了两物体构成的系统机械能守恒。
结论:
由于题目中说的是「轻杆」,说明其没有质量,所以该轻杆没有能量。那么它虽然可以做功,但做功得到的能量不能在其内部储存,所以它做的功必须传递到另一个物体中。所以轻杆相当于一个媒介,起到传递能量的作用。
综上所述,轻杆/轻绳总功一定为 \(0\)。借助此结论,当遇到类似本题的两物体题目时,若求得轻杆/绳对其中一个物体做功为 \(x\),则轻杆/绳对另一个物体的做功为 \(-x\)。
对于第三问:
由于问的是力,所以考虑对此时 \(2\) 物体受力分析有:
注意:
- 对于 \(2\) 的运动,\(r = \dfrac 2 3 L\) 而不是 \(L\)。
- 不能将第二问中轻杆做功的结论推到第三问力上,即此时轻杆对 \(1\) 的力并不能直接求得是 \(- \dfrac 9 5 m \mathrm g\),需要通过计算求得。
总结:
此题后两问求解时都会用到第一问的结论,实际上有些题目不一定会直接求第一问,而是直接求第二问,但是对于大题而言整体的做题步骤从第一问开始求是必要的。所以要遵循此类题目的解题步骤,这里的解题步骤在任何题目下都是通用的。
多物体动能定理
适用范围:所有的多物体题型。
解题步骤:相较于「多物体机械能守恒」除了将第 2 步的「列出能量守恒定律表达式」改为「列出整体的动能定理表达式」外,其它均无变化。
重要结论:轻杆/轻绳总功一定为 \(0\)。理由在上面已经说清楚,这里不做赘述。
示例:
这里以上述「多物体机械能守恒 - 基础题型示例」的第 1 问作为例题,示范「多物体动能定理」如何解题:
首先列出整体的动能定理表达式。对 \(1,2\) 整体从水平到竖直的整个运动段分析,由于轻杆做功一定为 \(0\),所以此时只有两物体的重力 \(G_1\) 和 \(G_2\) 做功,那么根据动能定理 \(W_合 = \Delta E_k\) 有
同样根据 \(v_1 = \dfrac 1 2 v_2\) 可求出 \(v_1\) 和 \(v_2\)。