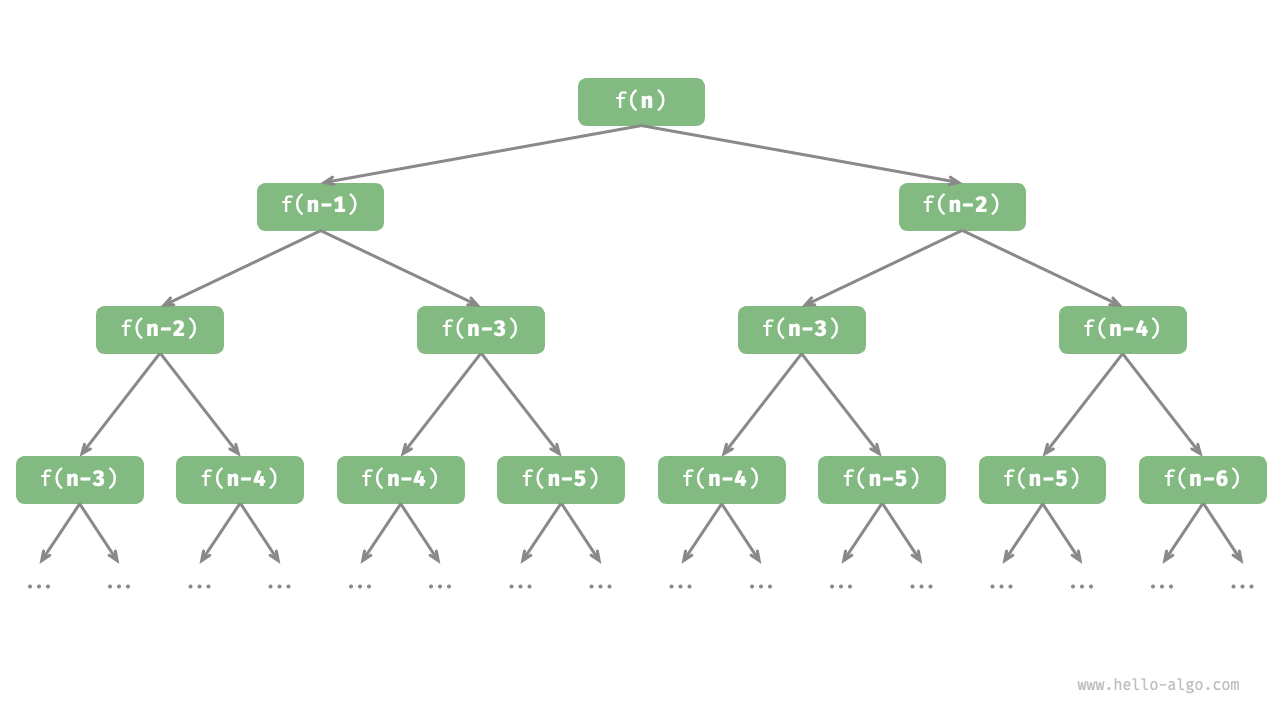
题意:一开始区间为[1, n],每次递归操作,如果区间长度<k则终止。如果当前区间长度为奇数,则加上mid,并递归[l, mid - 1] 和 [mid + 1, r];否则为偶数,则只进行递归[l, mid], [mid + 1, r]。
手搓几个样例发现是有点规律的。首先左右是对称的,左边加的数和右边一样多,只是大小不一样,再观察发现,对于每个区间的左右区间的数,右区间可以和左区间的数一一对应,为统一加了一个变量,然后发现这个变量是mid。那么可以递归求答案,求出左区间的贡献和产生贡献数的个数后,那么右边就是左区间贡献加上左区间个数×mid,并且个数要翻倍。区间长度为奇数的时候,贡献要加上mid,然后总个数加1.
点击查看代码
void solve() {i64 n, k;std::cin >> n >> k;auto dfs = [&](auto self, i64 n) -> std::pair<i64, i64> {if (n < k) {return {0, 0};}i64 mid = 1 + n >> 1ll;if (n & 1) {auto [sum, cnt] = self(self, mid - 1);return {2 * sum + cnt * mid + mid, 2 * cnt + 1};} else {auto [sum, cnt] = self(self, mid);return {2 * sum + cnt * mid, 2 * cnt};}};std::cout << dfs(dfs, n).first << "\n";
}