【C#】 SortedDictionary，查找字典中是否存在给定的关键字-编程知识

欢迎来到《小5讲堂》
这是《C#》系列文章，每篇文章将以博主理解的角度展开讲解。
温馨提示：博主能力有限，理解水平有限，若有不对之处望指正！

在这里插入图片描述

背景

最近有小伙伴咨询C#相关基础知识点SortedDictionary，
说实在的，这个类我也很少用，从字面上理解就是一个键值对，并且是含自动排序的键值对。
如果直接查询不存在的关键词，那么会直接报错，因此本篇文章来简单讲讲关键词判断

场景说明

SortedDictionary<TKey, TValue> 是C#中的一种集合类型，它实现了IDictionary<TKey, TValue> 接口，可以存储键-值对并按键排序。
SortedDictionary基于红黑树实现，因此其插入、删除和查找操作的复杂度为O(log n)，适合需要按键排序的场景。
SortedDictionary中的键必须是唯一的。
与Dictionary<TKey, TValue>不同的是，SortedDictionary会按键的比较顺序自动对键进行排序。
SortedDictionary比Dictionary有更高的查找开销，但可以提供快速的有序遍历。
可以使用SortedDictionary来存储需要按键排序的键值对，并快速查找、插入、删除和遍历它们。

红黑树原理

红黑树是一种自平衡的二叉搜索树，它在每个节点上都会增加一个额外的表示节点颜色的属性（通常为红色或黑色），并且满足以下几个性质：
1.每个节点要么是红色，要么是黑色。
2.根节点是黑色。
3.每个叶子节点（NIL节点，空节点）是黑色。
4.如果一个节点是红色的，则其子节点必须是黑色的。
5.从任一节点到其每个叶子节点的所有路径上，黑色节点的数量相同。
通过这些性质，红黑树保持了一种平衡，使得任何一条路径上的黑色节点数量差不多，从而确保了树的高度不会过高，最坏情况下的查找、插入和删除操作的时间复杂度为O(log n)。
红黑树的自平衡性质使得它在插入或删除节点时能够通过旋转和重新着色等操作来保持树的平衡。这种特性使得红黑树在需要频繁插入、删除操作的数据结构中具有很好的性能表现。

判断代码

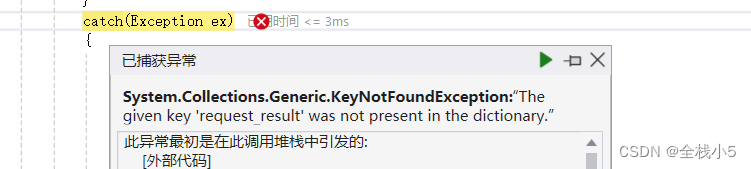
默认情况下，若不做判断会报错

The given key ‘request_result’ was not present in the dictionary.
字典中不存在给定的关键字“request_result”。

在这里插入图片描述

SortedDictionary<string, object> dict = new SortedDictionary<string, object>();// 添加一些键值对
dict.Add("key1", "value1");
dict.Add("key2", 123);
dict.Add("key3", true);// 判断是否包含关键词
string keyword = "key2";
if (dict.ContainsKey(keyword))
{Console.WriteLine($"Found keyword {keyword}");
}
else
{Console.WriteLine($"Keyword {keyword} not found");
}

Dictionary

在C#中，可以使用Dictionary<TKey, TValue>的ContainsKey方法来查找字典中是否存在给定的关键字。
该方法接受一个键作为参数，如果字典中包含该键则返回true，否则返回false。
下面是一个示例代码：

using System;
using System.Collections.Generic;class Program
{static void Main(){Dictionary<string, int> dictionary = new Dictionary<string, int>();dictionary.Add("apple", 1);dictionary.Add("banana", 2);string keyToFind = "banana";if (dictionary.ContainsKey(keyToFind)){Console.WriteLine($"The key '{keyToFind}' exists in the dictionary.");}else{Console.WriteLine($"The key '{keyToFind}' does not exist in the dictionary.");}}
}

在上面的示例中，创建了一个Dictionary<string, int>对象，并向其中添加了两个键值对。
然后我们使用ContainsKey方法来查找是否存在给定的关键字，并输出结果。

知识点

1.二叉查找树
二叉查找树（Binary Search Tree，BST），是一种二叉树，具有一定的排序性质，对于每个节点，左子树上所有节点的值都小于该节点的值，右子树上所有节点的值都大于该节点的值。在最坏情况下，BST的高度可能会达到O(n)，导致查找、插入和删除操作的时间复杂度变成O(n)。

2.AVL树
是一种自平衡的二叉搜索树，通过维护每个节点的平衡因子（左子树高度和右子树高度的差）为-1、0、1来保持树的平衡。AVL树确保了树的高度不会过高，从而保证了查找、插入和删除操作的时间复杂度为O(log n)。

3.B树和B+树
是一种多路搜索树，用于在内存和磁盘上存储大量数据。B树和B+树通过在一个节点中存储多个键值对来减少树的高度，从而减少查找的开销。B+树相比于B树更适合作为数据库索引的数据结构，因为B+树的叶子节点构成了一个有序链表，便于范围查询和范围遍历。

【C#】 SortedDictionary，查找字典中是否存在给定的关键字

【C#】.net core 6.0 MVC返回JsonResult显示API接口返回值不可被JSON反序列化

【C#】.net core 6.0 使用第三方日志插件Log4net，配置文件详细说明

【C#】使用代码实现龙年春晚扑克牌魔术（守岁共此时），代码实现篇

【C#】使用代码实现龙年春晚扑克牌魔术（守岁共此时），流程描述篇

【C#】约瑟夫原理举例2个代码实现

【C#】List泛型数据集如何循环移动，最后一位移动到第一位，以此类推

【C#】获取文本中的链接，通过正则表达式的方法获取以及优化兼容多种格式