无限集中的最小数字-编程知识

无限集中的最小数字

题目链接

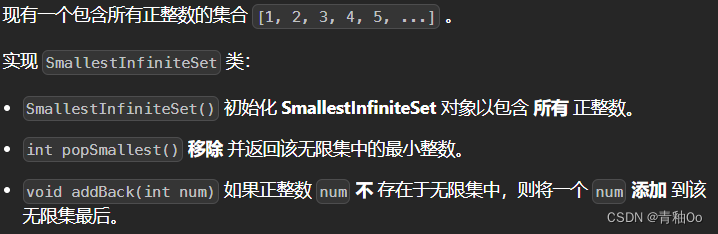
无限集中的最小数字

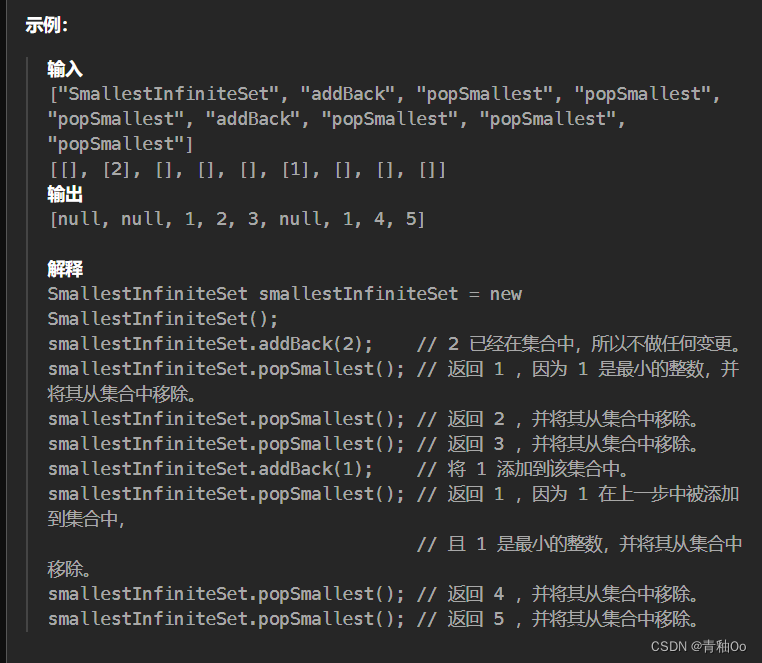
题目描述

注意点

1 <= num <= 1000

解答思路

由题意得，可以理解为最初集合中有1~1000之间的所有数字，如果集合中存在数字，则添加时不会有任何操作；在移除集合中的元素时，会按顺序从小到大进行移除，所以集合弹出的最大元素是有规律的，且始终保持为一个较小的元素，但是元素删除后可能又会添加到集合中，此时弹出的元素就不应该是弹出的最大元素加1，而是加入后的最小元素
使用noDelMin存储集合从未弹出元素的右边界（也就是最大值），使用TreeSet以从小到大的顺序存储被删除后又添加到集合中的元素
在进行添加操作时：如果添加的元素不小于noDelMin，说明该元素肯定还没有被弹出，不需要做任何操作；否则该元素已经被弹出（即使在这之前弹出后又添加，此时添加也无影响，TreeSet中元素不重复），需要重新添加到集合中，添加到TreeSet中
在进行删除操作时：如果此时TreeSet为空，说明此时没有元素被删除后又添加到集合中（即使有也说明该元素在这之前又被移除了），此时弹出的就是noDelMin；如果此时TreeSet不为空，说明此时有元素被删除在这之前又被添加到集合中，此时弹出的就是TreeSet的顶部元素

代码

class SmallestInfiniteSet {// 集合从未弹出元素的左边界int noDelMin;// 元素不重复，默认从小到大排序TreeSet<Integer> set;public SmallestInfiniteSet() {noDelMin = 1;set = new TreeSet<>();}public int popSmallest() {// set中有元素，可能是未删除过元素，也可能是删除元素后又添加进set中if (!set.isEmpty()) {return set.pollFirst();}// set中无元素，说明从1~delMax都被弹出，且删除后未添加进集合中，此时最小整数就是delMaxint res = noDelMin;noDelMin++;return res;}public void addBack(int num) {// num曾经被删除过又重新添加if (num < noDelMin) {set.add(num);}}
}