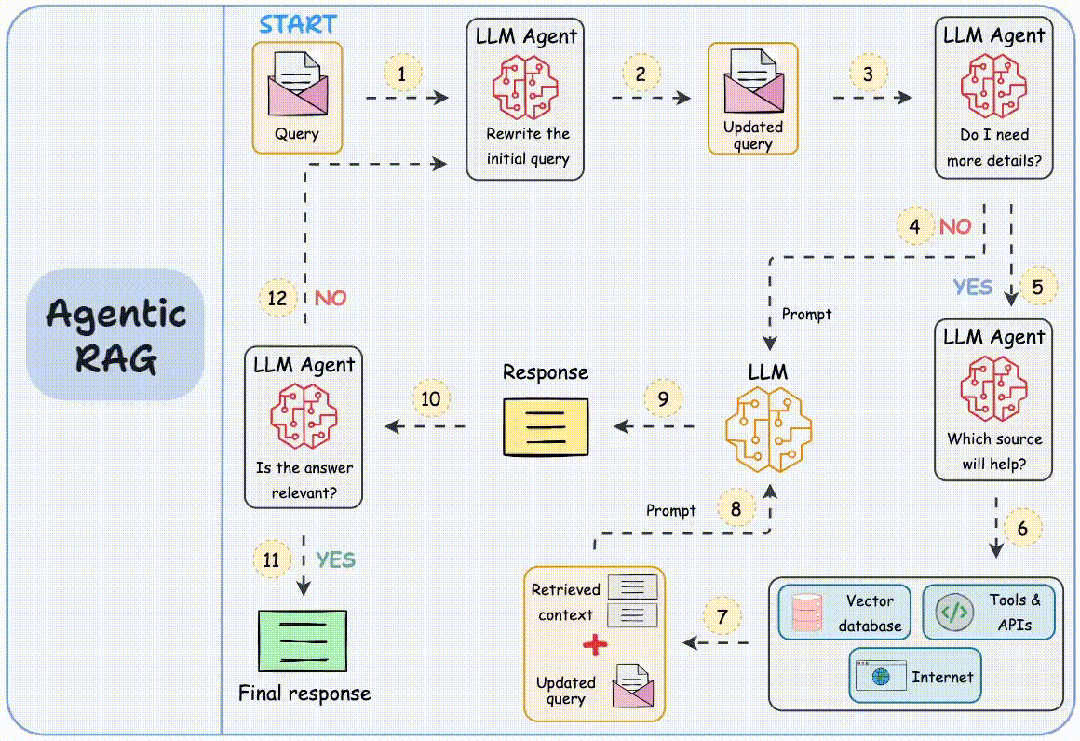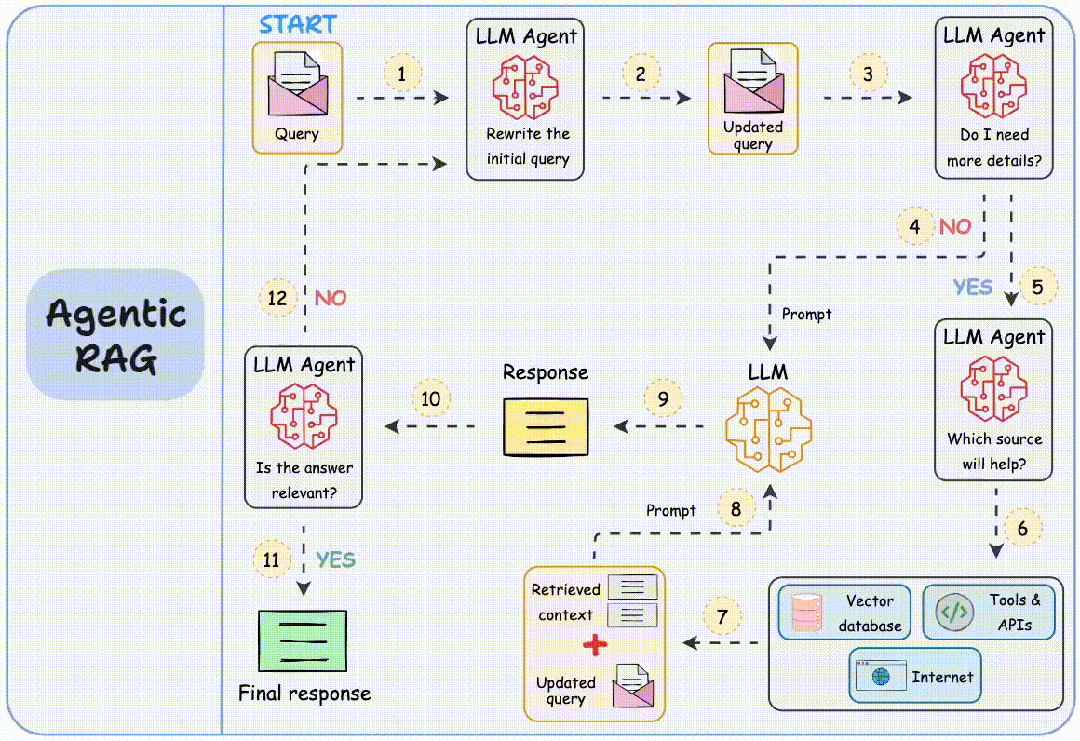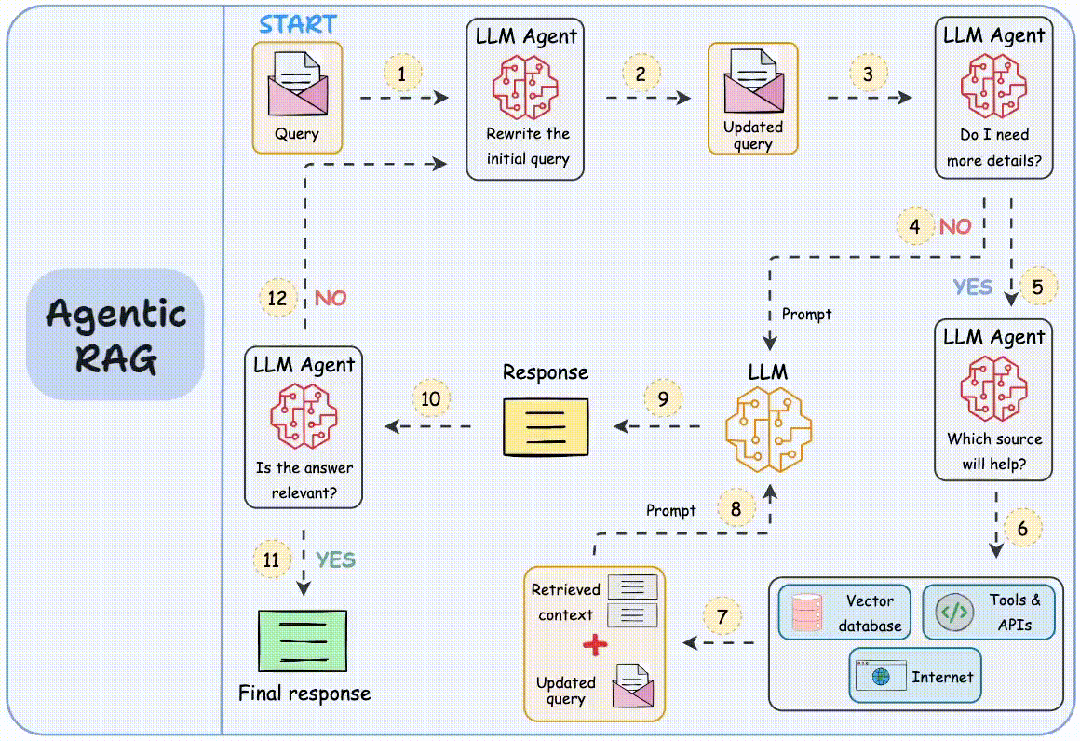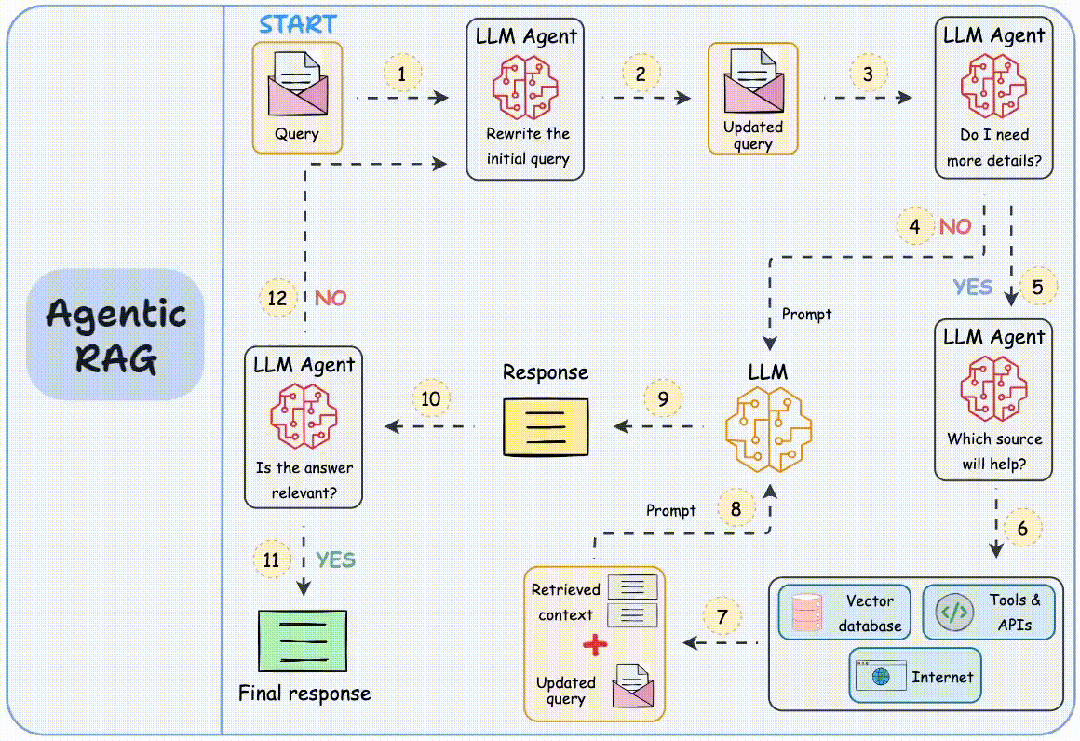
DAY1:贪心算法a
经典模型:
-
硬币问题:
找零钱问题:
有 \(100\) 元、\(50\) 元、\(20\) 元、\(10\) 元、\(5\) 元和 \(1\) 元这些面值的钱- 求凑出 \(𝑥\) 元的最多张数和最少张数,要求第 \(𝑖\) 种面值的钱不能用超过 \(𝑎_𝑖\) 张
- 多组询问,\(𝑇 ≤ 10^5,𝑎_𝑖 ≤ 10^9, 𝑥 ≤ 10^9\) 。
解题思路:
- 首先,我们需要将货币面值存储在一个数组中,按照从大到小的顺序排列,即 \(\{100, 50, 20, 10, 5, 1\}\) 。
- 对于求最多张数的情况:
- 从最小面值开始,尽可能多地使用该面值的货币,直到达到使用该面值的上限 \(a_i\) 或凑够所需金额 \(x\) 。
- 重复此过程,逐步使用更大面值的货币,直到凑够 \(x\) 元或无法再凑出。
- 对于求最少张数的情况:
- 从最大面值开始,尽可能多地使用该面值的货币,直到达到使用该面值的上限 \(a_i\) 或凑够所需金额 \(x\) 。
- 重复此过程,逐步使用更小面值的货币,直到凑够 \(x\) 元或无法再凑出。
-
部分背包
例如: -
区间问题
- 选择若干不相交区间问题
-
例题:
-
思路: 以结束时间为第一关键字排序,依次考虑各个活动,如果没有和已经选择的活动冲突,就选,否则就不选。
-
- 区间覆盖或线段覆盖问题
-
例题:
-
思路: 最左边的线段放什么最好?
显然放右端点最靠左的线段最好,从左向右放,右端点越小妨碍越少。
其他线段放置按右端点排序,贪心放置线段,即能放就放。(类似若干不相交区间问题)
-
- 区间分段问题
-
例题:
-
思路: 这个应该算是最简单最基础的贪心了,甚至都不用排序,从前往后扫,一旦和大于 \(m\) ,再分新的一段。
-
- 选择若干不相交区间问题
-
顺序问题
一般解题步骤
- 建立数学模型来描述问题(把问题简化成学过的知识,术语,或者算法);
- 把求解的问题分成若干个子问题(大事化小);
- 对每一子问题求解,得到子问题的局部最优解(小事化了);
- 把子问题的局部最优解合成原来问题的一个解(合并所有答案得到最终答案)。
范围及证明
决定一个贪心算法是否能找到全局最优解的条件:
-
\({\color{Blue}\large \mathcal{有最优子结构}}\):很好理解,就是指一个问题的最优解包含其子结构的最优解,和动态规划上理解是一样的。
-
\({\color{Blue}\large \mathcal{有最优贪心选择属性}}\):而贪心选择性是指所求问题的整体最优解可以通过一系列可以通过一系列局部最优的选择来达到。他总是作出当前最好的选择,该选择可以依赖于之前的选择,但绝不依赖于将来的选择和子问题的选择,这是他与动态规划的重要区别。
一般我们证明一个题目可以用贪心就是证明上面两点均满足。
-
反证法: 如果交换方案中任意两个元素/相邻的两个元素后,答案不会变得更好,那么可以推定目前的解已经是最优解了。
-
归纳法: 先算得出边界情况(例如 \(n=1\) )的最优解 \(F_1\) ,然后再证明:对于每个 \(n\) ,\(F_{n+1}\) 都可以由 \(F_n\) 推导出结果。
归纳法例题:
题目解法&思路
\(T1\)
#include <bits/stdc++.h>
using namespace std;struct node{int x,y;
}a[101010];
int n;
bool cmp(node xx,node yy){return xx.y < yy.y;
}
int main(Designer = 洛谷@Lwj54joy,uid=845400){cin>>n;for(int i = 1;i <= n;i++){cin>>a[i].x>>a[i].y;}sort(a+1,a+1+n,cmp);int ans = 1,ls;ls = a[1].y;for(int i = 2;i <= n;i++){if(a[i].x >= ls) ans++,ls = a[i].y;}cout<<ans<<endl;
}
\(T2\)
#include <bits/stdc++.h>
using namespace std;
bool f[101010];
struct node{int x,y,z;
}a[101010];
int n;
bool cmp(node xx,node yy){return xx.y < yy.y;
}
int h;
int main(Designer = 洛谷@Lwj54joy,uid=845400){cin>>n>>h;for(int i = 1;i <= h;i++){cin>>a[i].x>>a[i].y>>a[i].z;}sort(a+1,a+1+h,cmp);int ans = 0;for(int i = 1;i <= h;i++){int lim = a[i].z;for(int j = a[i].x;j <= a[i].y and lim;j++){if(f[j]) lim--;}if(lim != 0){for(int j = a[i].y;j >= a[i].x and lim;j--){if(f[j]) continue;ans++;f[j] = true;lim--;}}}cout<<ans<<endl;
}
\(T3\)
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>struct node {double l, r;bool operator<(const node& W) const {return l < W.l;}
};int main(Designer = 洛谷@Lwj54joy,uid=845400){int T;std::cin >> T;while (T--) {int cnt = 0;int n;double l, w;std::cin >> n >> l >> w;std::vector<node> a;double w2 = w / 2.0;for (int i = 0; i < n; ++i) {double x, y;std::cin >> x >> y;if (y <= w / 2) {continue;}node temp;temp.l = x - std::sqrt(y * y - w * w / 4);temp.r = x + std::sqrt(y * y - w * w / 4);a.push_back(temp);}std::sort(a.begin(), a.end());double s = 0, e = l;int i = 0, ans = 0;bool t = false;while (s < e) {double vis = -2e9;size_t j;for (j = i; j < a.size(); ++j) {if (a[j].l <= s) {vis = std::max(vis, a[j].r);} else {break;}}if (s < e && vis < s) {std::cout << -1 << "\n";t = true;break;}ans++;s = vis;i = j;}if (!t) std::cout << ans << "\n";}}
\(T4\)
#include <bits/stdc++.h>
using namespace std;
struct node{int w,id;
}e[1010];
int a[1010],b[1010],n;
bool cmp(node xx,node yy){return xx.w < yy.w;
}
int main(Designer = 洛谷@Lwj54joy,uid=845400){cin>>n;for(int i = 1;i <= n;i++) cin>>a[i];for(int i = 1;i <= n;i++) cin>>b[i];for(int i = 1;i <= n;i++) e[i] = {min(a[i],b[i]),i};sort(e+1,e+1+n,cmp);int q[1010] = {0},l = 0,r = n+1;for(int i = 1;i <= n;i++)if(e[i].w == a[e[i].id]) q[++l] = e[i].id;else q[--r] = e[i].id;int ta = 0,tb = 0;for(int i = 1;i <= n;i++){ta += a[q[i]];tb = max(ta,tb);tb += b[q[i]];}cout<<tb<<endl;
}
\(T5\)
#include <bits/stdc++.h>
using namespace std;struct node{int t,w;bool operator<(const node &W) const{return w>W.w;}
}a[1010];
bool st[1010];
int n,m;
int main(Designer = 洛谷@Lwj54joy,uid=845400){cin>>m>>n;for(int i = 1;i <= n;i++) cin>>a[i].t;for(int i = 1;i <= n;i++) cin>>a[i].w;sort(a+1,a+1+n);for(int i = 1;i <= n;i++){bool flag = false;for(int k = a[i].t;k >= 1;k--){if(!st[k]){flag = true;st[k] = 1;break;}}if(!flag) m -= a[i].w;}cout<<m<<endl;
}
\(T6\)
#include <bits/stdc++.h>
using namespace std;
int a[1110100];
int n;
struct cmp1{bool operator()(int x,int y){return x < y;}
};
struct cmp2{bool operator()(int x,int y){return x > y;}
};
int main(Designer = 洛谷@Lwj54joy,uid=845400){priority_queue<int,vector<int>,cmp1> q1; //大根堆priority_queue<int,vector<int>,cmp2> q2; //小根堆 cin>>n;for(int i = 1;i <= n;i++){cin>>a[i];q1.push(a[i]);q2.push(a[i]); } while(q1.size() >= 2){int xx = q1.top(); q1.pop();int yy = q1.top();q1.pop();q1.push(yy*xx+1);}while(q2.size() >= 2){int xx = q2.top(); q2.pop();int yy = q2.top();q2.pop();q2.push(yy*xx+1);}cout<<q2.top() - q1.top()<<endl;
}
\(T7\)
#include <bits/stdc++.h>
using namespace std;int a[101010];
int n,m;
int main(Designer = 洛谷@Lwj54joy,uid=845400){cin>>n>>m;for(int i = 1;i <= n;i++){cin>>a[i];}int ans = 1,kkk = 0;for(int i = 1;i <= n;i++){if(kkk+a[i] <= m) kkk += a[i];else kkk = a[i],ans++;}cout<<ans<<endl;
}
\(T8\)
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;struct node{int x,y;
}a[1010010];
int n;
bool cmp(node xx,node yy){return xx.y < yy.y;
}
int main(Designer = 洛谷@Lwj54joy,uid=845400){cin>>n;for(int i = 1;i <= n;i++){scanf("%d%d",&a[i].x,&a[i].y );}sort(a+1,a+1+n,cmp);int ans = 1,ls;ls = a[1].y;for(int i = 2;i <= n;i++){if(a[i].x >= ls) ans++,ls = a[i].y;}cout<<ans;
}
\(T9\)
#include <bits/stdc++.h>
using namespace std;
int n,leisure,fish[200],trip[1010],delta[1010];
struct node{int id,key;bool operator < (const node &rhs)const{return key<rhs.key;}
};
int main(Designer = 洛谷@Lwj54joy,uid=845400){cin>>n>>leisure;leisure *= 12;node t;int answer = -1;for(int i = 1;i <= n;i++){cin>>fish[i];}for(int i = 1;i <= n;i++){cin>>delta[i];}for(int i = 1;i < n;i++){cin>>trip[i];trip[i] += trip[i-1];}int lt,ans;for(int i = 1;i <= n;i++){lt = leisure-trip[i-1],ans = 0;priority_queue<node> q;for(int j = 1;j <= i;j++) q.push({j,fish[j]});for(int j = 1;j <= lt;j++){t=q.top();q.pop();if(t.key < 0) break;ans += t.key;q.push({t.id,t.key-delta[t.id]});}answer = max(answer,ans);}cout<<answer<<endl;
}
\(T1\)
#include <bits/stdc++.h>
using namespace std;int a[1010101];
long long c[1010101];
long long sum,n;
int main(Designer = 洛谷@Lwj54joy,uid=845400){cin>>n;for(int i = 1;i <= n;i++){scanf("%d",&a[i]);sum += a[i];}long long ave = sum/n;for(int i = n;i >= 1;i--) c[i] = c[i+1]+ave-a[i];c[1] = 0;sort(c+1,c+1+n);long long ans = 0;for(int i = 1;i <= n;i++){ans += abs(c[i]-c[(n+1)/2]);}cout<<ans<<endl;
}