目录
题目
方法一
思路
优化
方法二
思维误区
递归关系推导
代码实现
题目
98. 验证二叉搜索树
难度:中等
给你一个二叉树的根节点root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
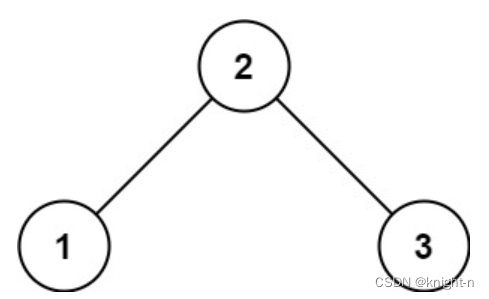
输入:root = [2,1,3]
输出:true
示例 2:
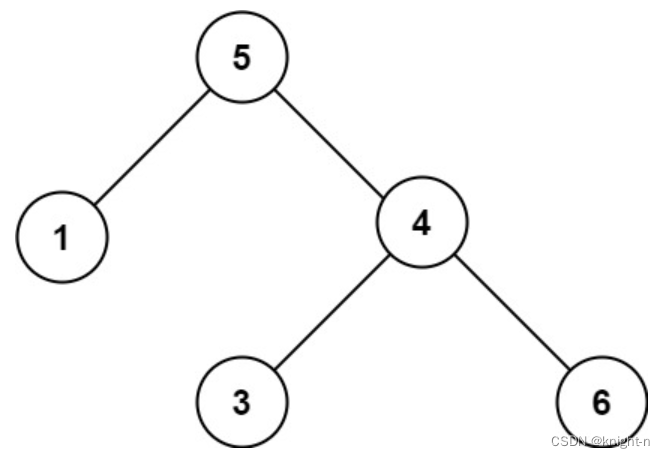
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
方法一
思路
我们知道一个二叉搜索树的中序遍历得到的序列一定是升序的。那么我们直接中序遍历二叉树,将每个结点的值保存,然后判断得到的序列是否升序即可。这种方法的时间复杂度和空间复杂度均为O(n)。
Q:为什么中序遍历一颗二叉树得到升序序列可以证明这颗树是二叉搜索树?
A:二叉搜索树的定义是:对于树中的每个节点,它的左子树中的所有节点的值都小于该节点的值,而它的右子树中的所有节点的值都大于该节点的值。这个特性保证了二叉搜索树在结构上有序。而中序遍历二叉树的顺序是:先遍历左子树,然后访问根节点,最后遍历右子树。由于二叉搜索树的左子树节点值小于根节点,右子树节点值大于根节点,因此中序遍历二叉搜索树的结果会是一个升序序列。反过来,如果中序遍历一颗二叉树得到的是升序序列,那么这颗树的每个节点的左子树节点值都小于它,右子树节点值都大于它,这符合二叉搜索树的定义。
A:当访问任意节点A时,肯定已经先访问了A的左子树,因为得到的是升序序列,此时A的值大于左子树所有的值,A和左子树满足二叉搜索树的定义,同理A和右子树满足二叉搜索树的定义,所以以A为根节点数是二叉搜索树。所以这颗树满足二叉搜索树的定义,是一颗二叉搜索树。
优化
这个算法还可进一步优化,判断输出序列是否升序仅需检查当前节点的值是否大于前一个中序遍历到的节点的值即可。所以我们仅需保存上一个结点的值即可。这种方法的时间复杂度为O(n),时间复杂度均为O(1) (忽略函数调用栈空间)。
这种方法很容易想到,实现也很容易,在此我们不具体实现。如果大家对二叉树的遍历不熟悉,可以参考我的往期博客:二叉树的遍历。
方法二
思维误区
通过搜索二叉树的性质:对于树中的每个节点,它的左子节点值小于该节点的值,而它的右子节点的值大于该节点的值。我们很容易想出一个递归算法,即递归判断每个结点的左子结点和右子结点,判断他们是否小于或大于父节点的值。如果所有结点都符合条件,则该树为二叉搜索树。
其实这是一个经典的思维误区,我们举一个反例:
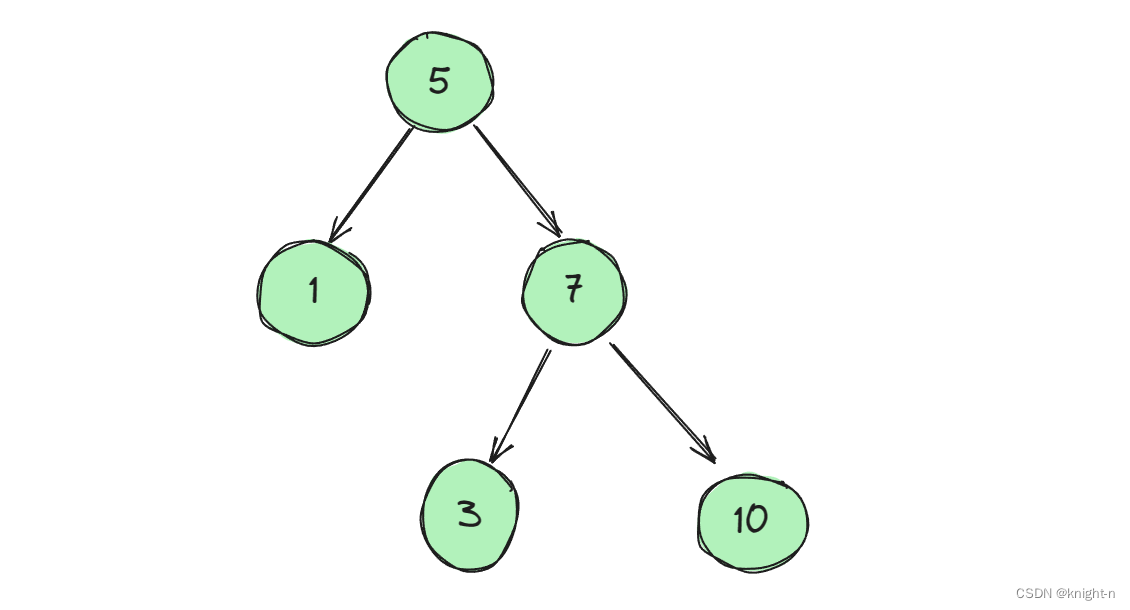
对于这颗树它的树中的每个节点,它的左子节点值小于父节点的值,而它的右子节点的值大于该节点的值。但他并不是一个二叉搜索树。
为什么呢?因为二叉搜索树定义中
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
也就是说每个结点的左子节点的上界为当前节点,右子节点的下界为当前节点。同时他们还需要有一个下界/上界,保证他们符合二叉搜素树的定义。
那么我们现在只要知道左子节点的下界,右子节点的上界。就可以得出递归关系,进行递归判断。
递归关系推导
对于二叉树中的结点(除根节点,与其左右结点)都可概括为以下四种类型:
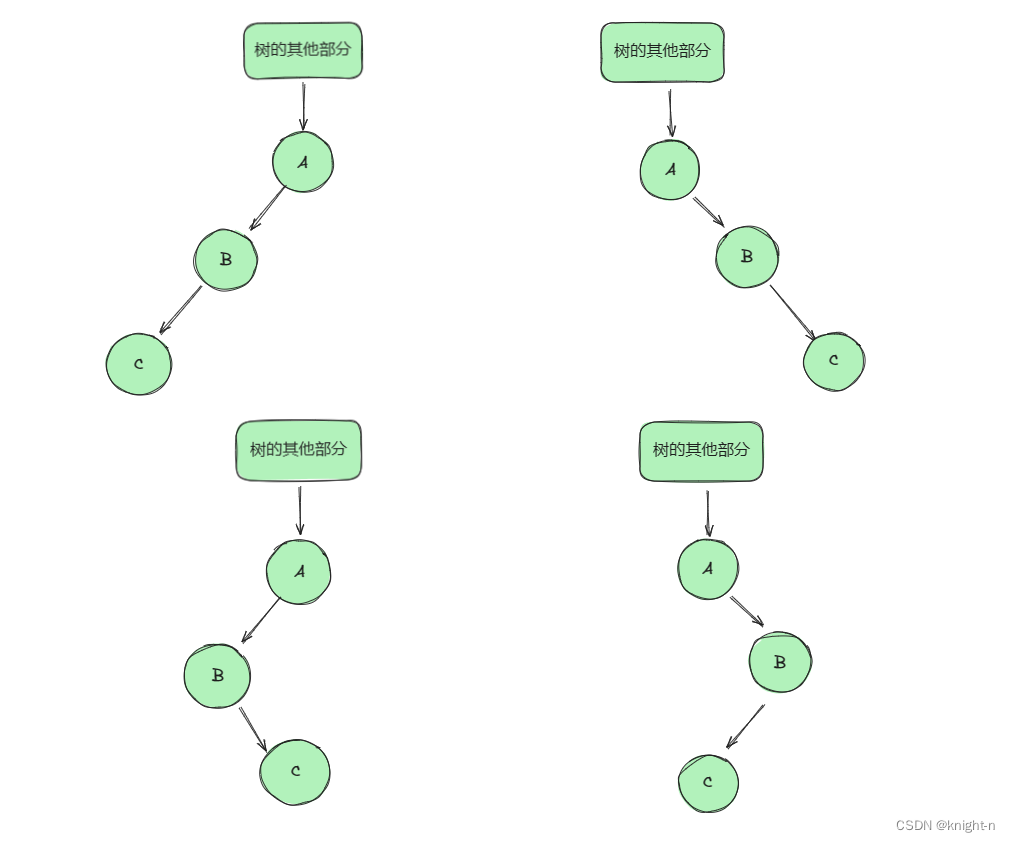
我们先分析C作为B左子树的两种情况:
情况一:
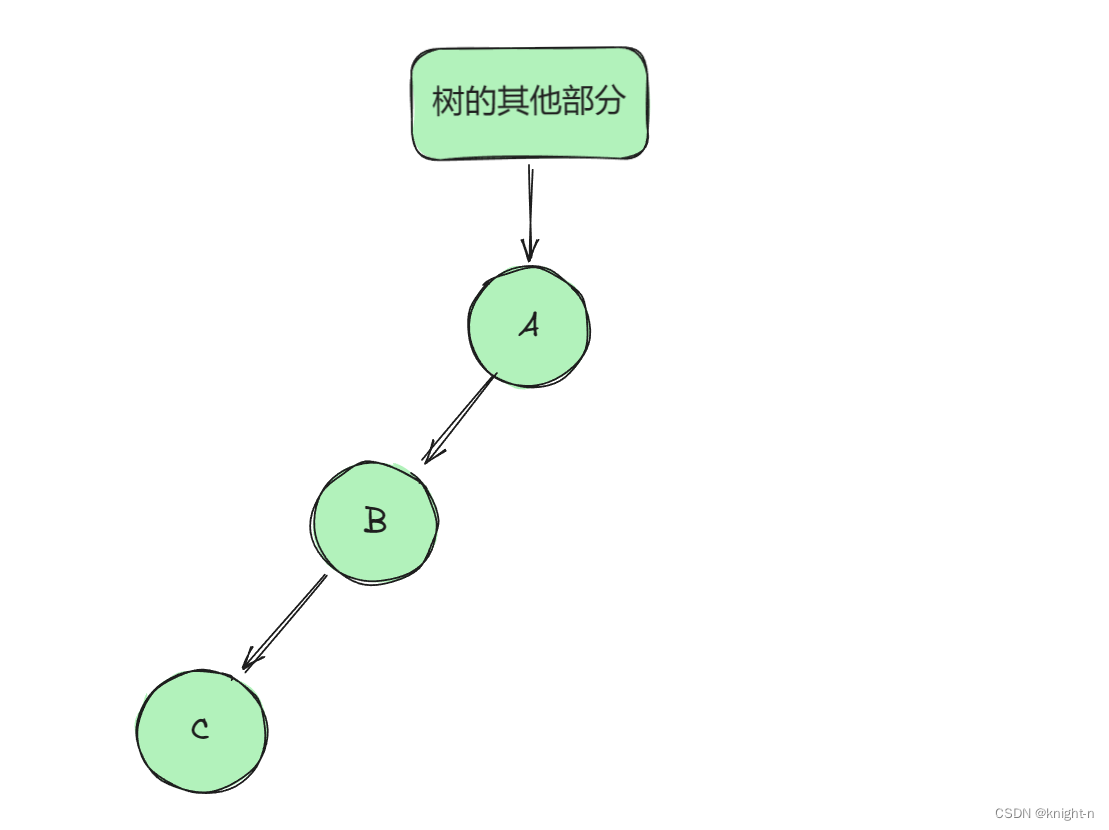
情况二:
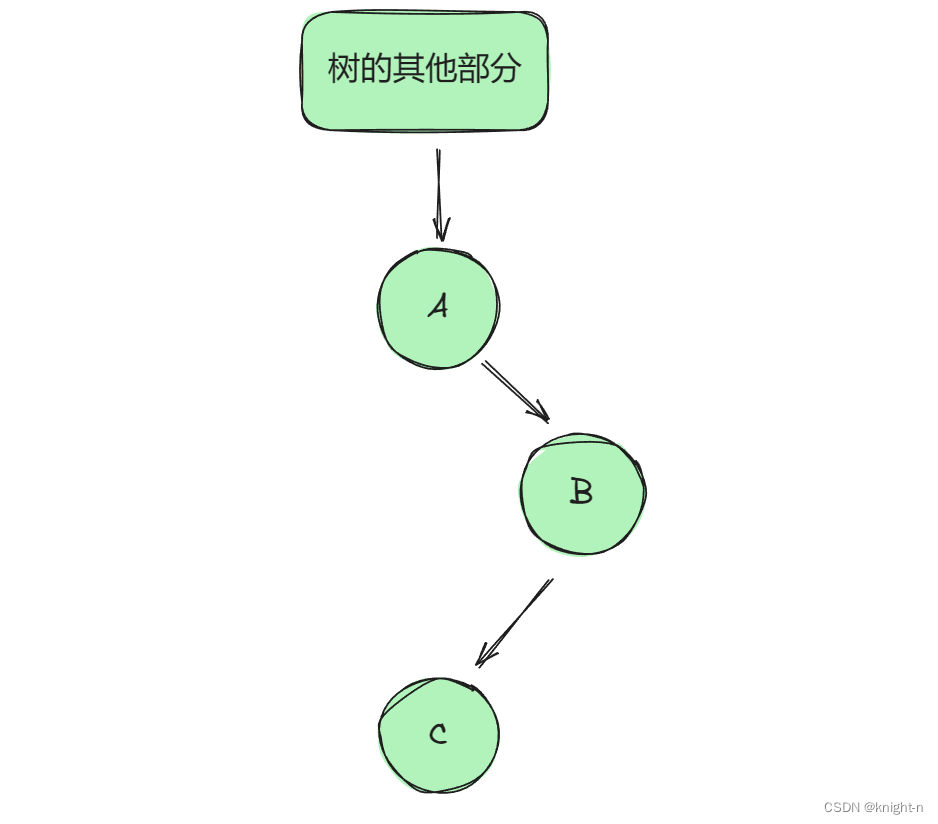
上界:对于这两种情况 ,C 都要小于 B ,即 C 的上界为 B。
下界:情况一下,C 的下界为负无穷。B的下届也为负无穷。即 C 的下界为 B 的下界。情况二下,C 必须小于 A,即 C的下界为A。B的下界也为A, 即 C 的下界为 B 的下界.
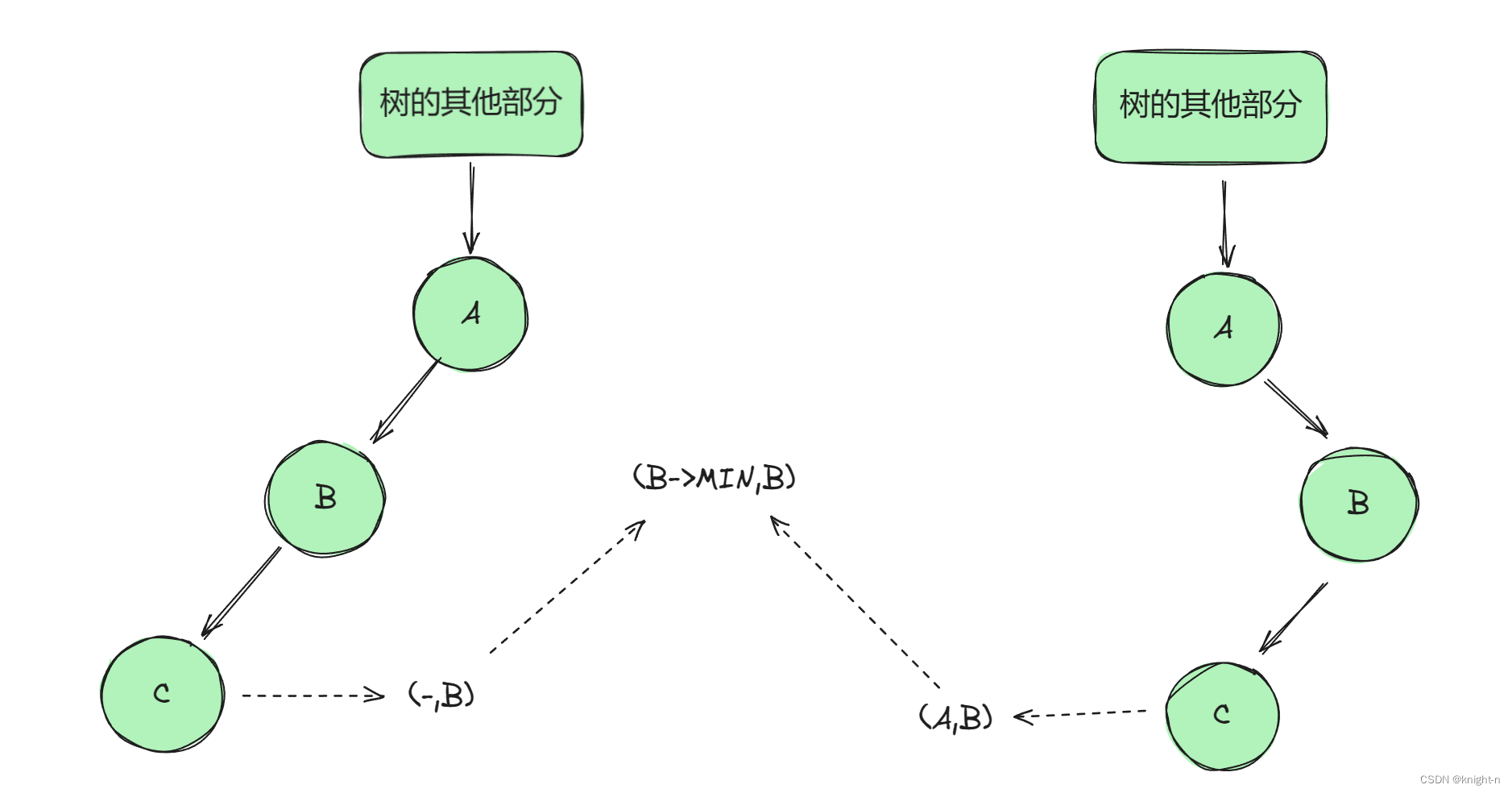
综上可得:当前结点的左子节点的上界为当前节点,下界为当前节点的下界。
C作为B右子树的两种情况:
情况一:
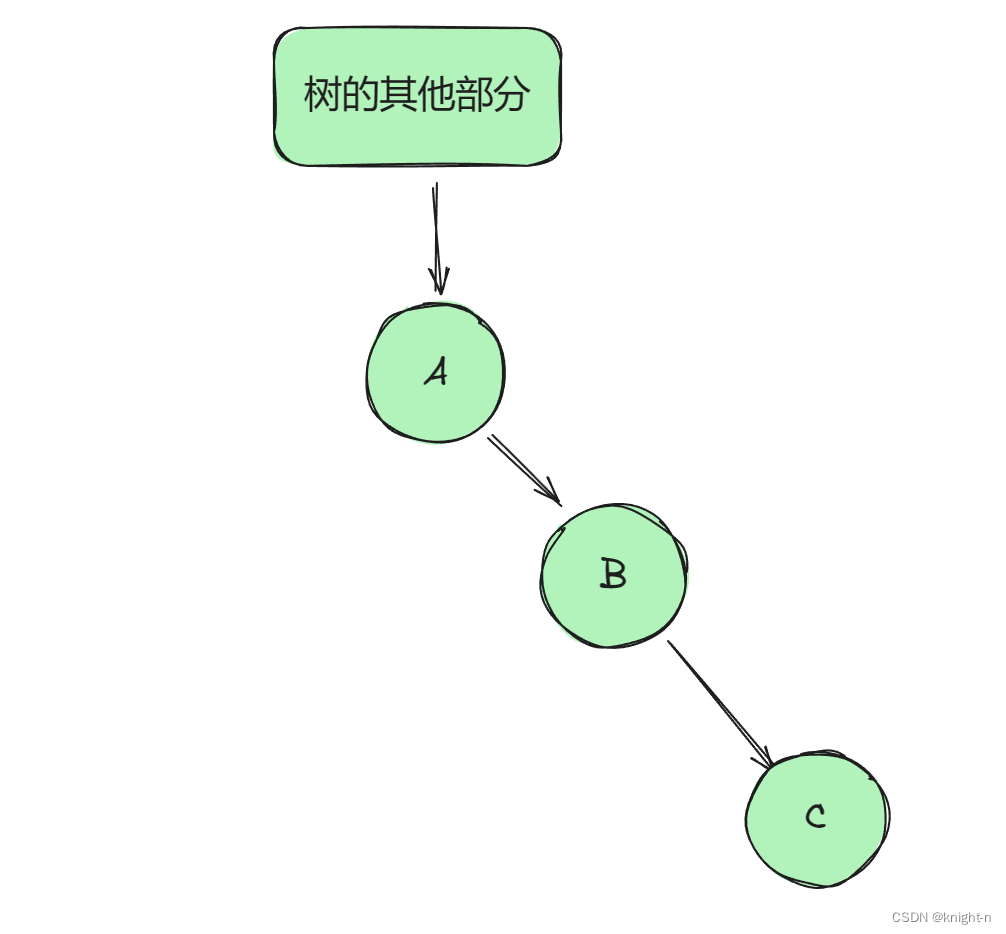
情况二:
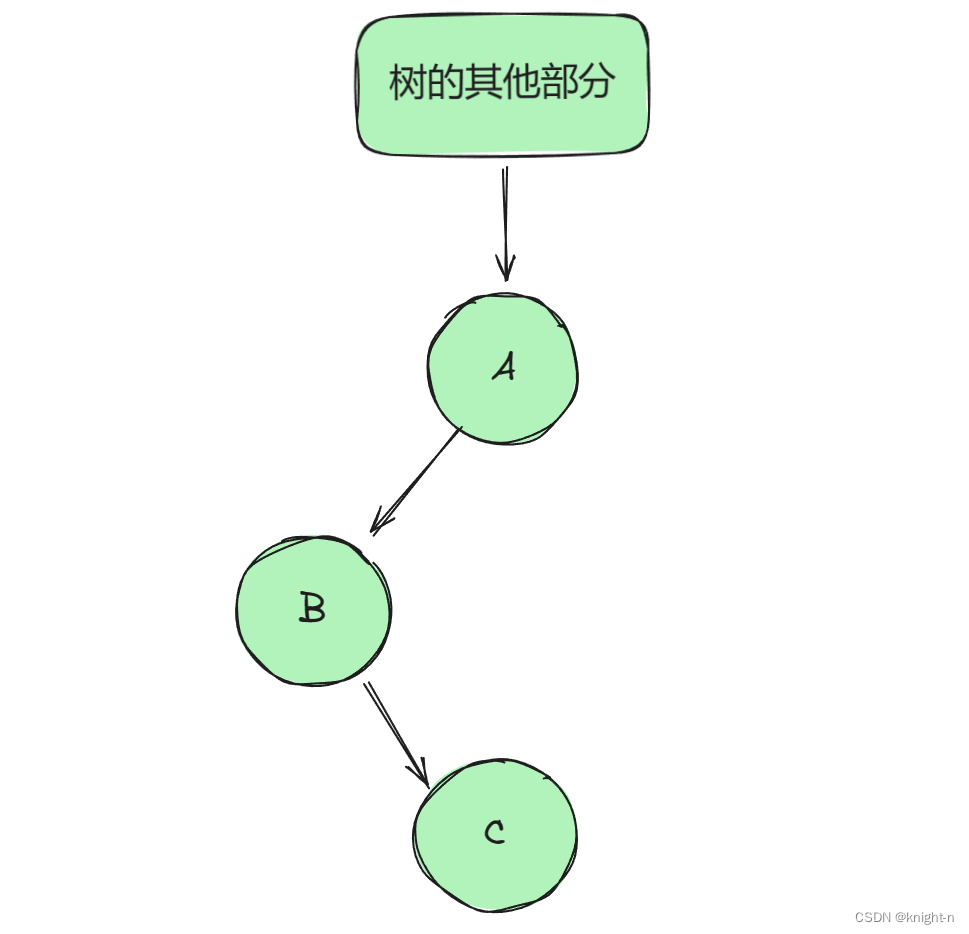
上界: 情况一下,C 的上界为正无穷。B的上界届也为正无穷。即 C 的上界为 B 的上界。情况二下,C 必须小于A,即 C的上界为A。B的上界也为A, 即 C 的上界为 B 的上界.
下界:对于这两种情况 ,C 都要大于 B ,即 C 的下界为 B。
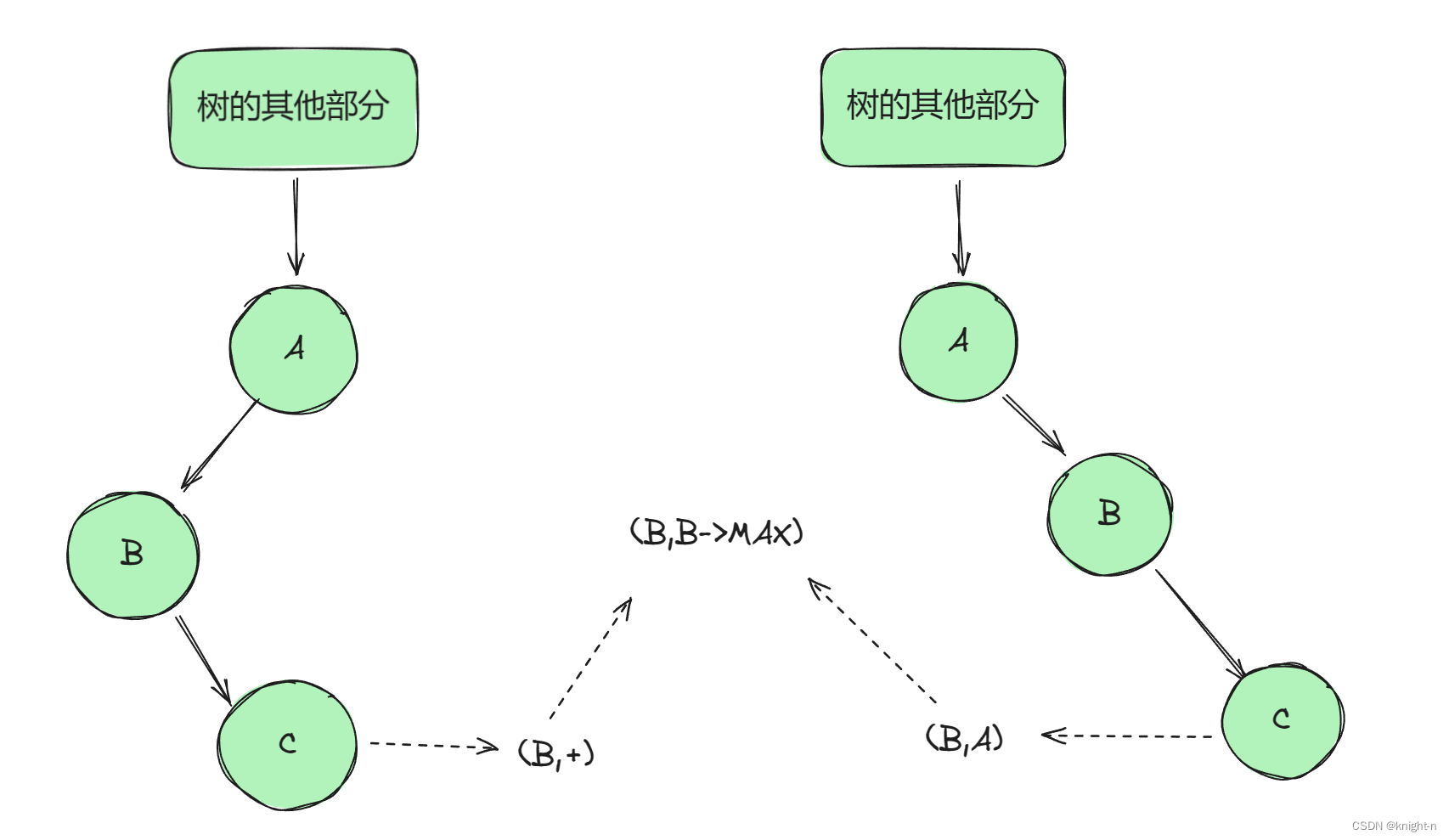
综上可得:当前结点的右子节点的下界为当前节点,上界为当前节点的上界。
代码实现
现在我们得到了递归关系,只需递归判断左右子树即可。
代码如下:
class Solution {
public:bool istrue(TreeNode* root,long long min,long long max){if(!root) return true;if(root->val<=min || root->val>=max){return false;}return istrue(root->left,min,root->val) && istrue(root->right,root->val,max);//[min,root->val] [root->val,max]}bool isValidBST(TreeNode* root) {return istrue(root,LONG_MIN,LONG_MAX);}
};