算法题解记录25+++验证二叉搜索树（百日筑基）-编程知识

题目描述：

难度：中等

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左
子树
只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

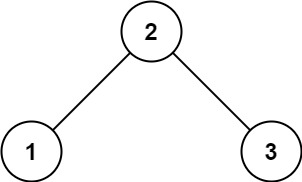
输入：root = [2,1,3]
输出：true

示例 2：

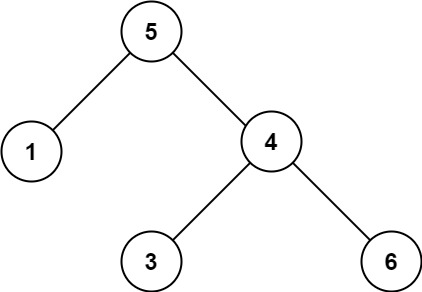
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 10^4] 内
-2^31 <= Node.val <= 2^31 - 1

解题准备：

1.题意：题目要求验证一棵二叉树，是不是二叉搜索树（BST，即Binary Search Tree），那么我们首先要知道，一棵二叉搜索树是什么样的。

简单地说，BST有如下性质：第一，其左子树上所有节点的值，都小于根节点值；第二，其右子树上所有节点的值，都大于根节点的值。第三，BST下所有节点，都有BST的性质。

2.基本操作：就题目看，不涉及增删改，验证必然要涉及查找遍历，姑且认为只有查找和比较。

3.基础原理：面对树的题目，我们应敏锐地察觉到至少两种方法---BFS广度优先搜索和DFS深度优先搜索。这两种方法几乎是树的算法的基础，大多数算法，都是在二者之上优化而得。

解题思路：

朴素地说，对于新手，其实一看到这个题目，是不会有什么思路的。

然而，如果说做过一些题，就能直接得到答案，也非常夸张。

我在此分享我的错误思路。

错误思路---左右递归判断

我最开始的思路比较简单，基于两个基本原理：

第一，如果一棵树左子节点left的值，大于或等于根节点root的值，说明它不是BST。

第二，如果一棵树右子节点right的值，小于或等于根节点root的值，说明不是BST。

这两个原理没有错，却不完全，如果一棵树满足这两个原理，也有可能不是BST，比如下图，7大于5，却满足这个原理，同样，3小于5，也满足这个原理。

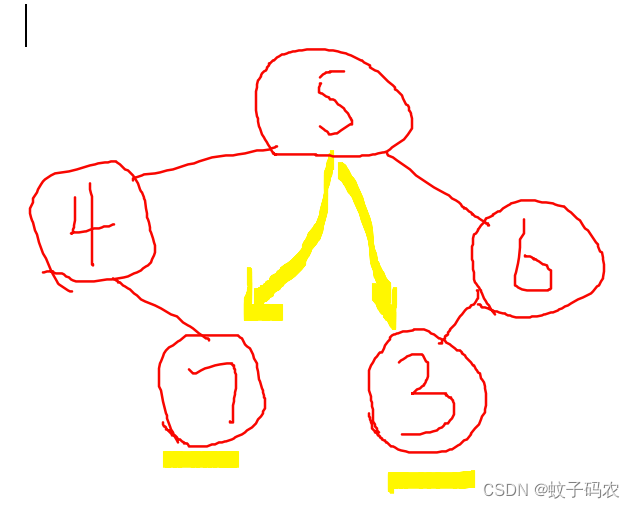
这两个原理没有满足整体，所以我编写的代码在运行之后也报错了，不过，我会在下面提供代码。我先在此说明我的思考过程。【如何将这两个原理转化为代码的】

第一步，有了原理，尽量往dfs或者bfs方法上靠近。

第二步，发现判断一个节点是否满足2个原理，只需要判断left与root的关系、right与root的关系即可。【异常处理还没做】

第三步，得到问题：虽然判断一个节点很简单，怎么判断下一个呢？

第四步，初始的朴素思想：干脆中序遍历或前序遍历一遍，得到所有节点（存储List），依次进行判断？

第五步，想到优化思路，既然中序遍历能够遍历每个节点，为什么要遍历一边，然后又从List再遍历一遍？

第六步，中序原理是左根右，访问操作只在根节点做，那么继续左中右方法，把判断左子放在“左”，判断右子放在“右”，根节点的数据访问忽略了，就可以了。

第七步，异常：访问到空节点null。

第八步：if限制，null节点直接返回，又因为要判断子节点与根节点的关系，返回明显不能处理，所以需要额外判断子节点是否为null。

完成。

正确思路---中序遍历序列

这个思路首先要明白一件事：中序遍历，其顺序是左子树、根节点、右子树。

其中，在左子树left中，其顺序也是left的左子树、left、left的右子树。

如果一棵树只有一个节点，毫无疑问它是升序的。

假设这棵树root，它的左子树是left，右子树是right。

那么，中序遍历时，一定会访问到left的最左子节点X，它是升序的。

接着，访问最左子节点的父节点F，由于BST性质，最左子X小于F，所以是升序的。

然后，访问F的右子【也有可能是右子的左子、右子的左子的左子……】P，由于BST性质，XFP升序排列。

由于这棵树升序排列，那么，它的父树也升序排列，最后，left升序排列，整个节点的中序序列，都升序排列。

由此，我们只需要得到中序序列，即可判断。

正确思路---区间逼近

这个思路是题解的思路，不过与我的错误思路非常接近，它把我的2个原理推进了。

原理1：左子节点left，一定比root小，左子的左子，一定比root小；左子的右子，一定比root小，并且比左子大……

原理2：右子节点right，一定比root大，右子的右子，一定比root大；右子的左子，一定比root大，并且比右子小。

如此，我们可以发现，我的错误思路，就在于判断时，只是把节点与其左右子进行判断，忽略了最重要的根节点。

然而，问题出现了：如果我们持续用root的值，作为判断依据，如下图：5作为右边所有节点的下限，没有问题，但是9却比7要大，也就是说子树7不符合BST的性质，所以整棵树不是BST。

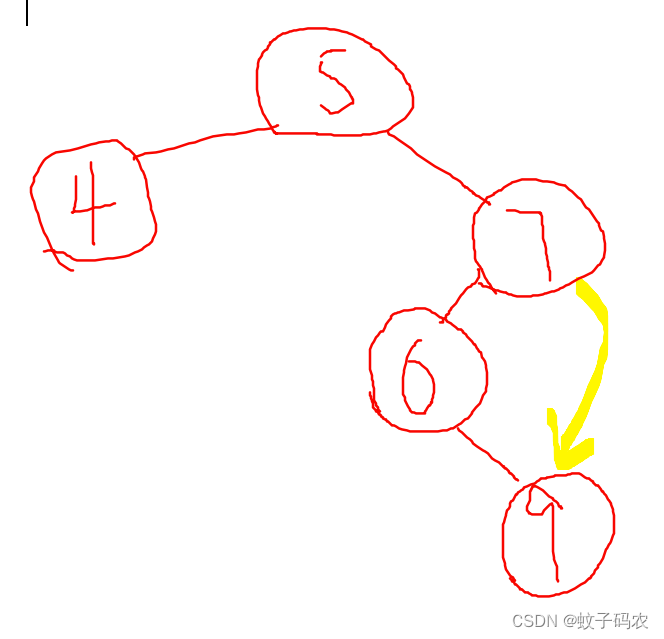
换句话说，我们要求上下限是不断变化的，这其实也是二叉树的精髓部分。

怎么做呢？

一般的想法是，维护两个变量low、up，使它们代表某个节点的上下限，在每次判断时作为依据。

不过，如果这两个变量只是代表1个节点上下限，那么我们要开辟一个非常大的空间，用来存储所有的变量对low、up。

所以，借助递归的方案，我们把维护变量对的操作交给系统，我们只需要递归调用时，传递变量对即可。

解题难点分析：

无

错误代码---我的思路：

class Solution {public boolean isValidBST(TreeNode root) {boolean flag = true;// 为null不判断if(root.left!=null){if(root.left.val>=root.val){return false;}flag = isValidBST(root.left);}// 看一下是否不是BSTif(!flag){return flag;}// 同理if(root.right!=null){if(root.right.val<=root.val){return false;}flag = isValidBST(root.right);}return flag;}
}

代码---中序遍历：

class Solution {public boolean isValidBST(TreeNode root) {// 存储节点List<Integer> data = new ArrayList<>();fuzhu(root, data);// 依次判断for(int i=0; i<data.size()-1; i++){if(data.get(i) >= data.get(i+1)){return false;}}return true;}private void fuzhu(TreeNode root, List<Integer> data){if(root==null){return;}fuzhu(root.left, data);data.add(root.val);fuzhu(root.right, data);}
}

代码---迭代上下限：

class Solution {public boolean isValidBST(TreeNode root) {return fuzhu(root, Long.MIN_VALUE, Long.MAX_VALUE);}private boolean fuzhu(TreeNode root, long low, long up){// 如果是空节点，即正确 if(root==null){return true;}// 如果超出界限，则错误// 我们可以看出来，每次递归判断，只能判断一个节点，我们不可能一起判断左子和右子if(root.val <= low || root.val >= up){return false;}// 返回左子节点、右子节点的判断。return fuzhu(root.left, low, root.val) && fuzhu(root.right, root.val, up);}
}

以上内容即我想分享的关于力扣热题25的一些知识。

我是蚊子码农，如有补充，欢迎在评论区留言。个人也是初学者，知识体系可能没有那么完善，希望各位多多指正，谢谢大家。