摘要：搜索二叉树的效率，搜索二叉树的两种搜索模型及应用举例

前面一片文章学习了并实现了搜索二叉树，这篇将从实际应用的角度进一步介绍搜索二叉树。

---

1. 搜索二叉树的效率

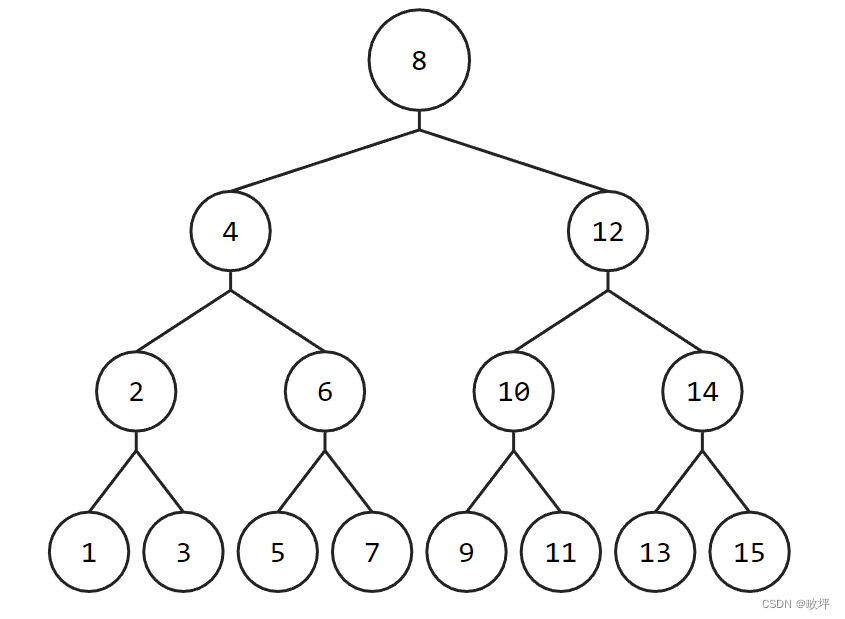
BST的查找效率是 O(N)。
分析：如右图所示的二叉树中，如果我们需要查找结点1，则我们需要遍历所有的结点才能找到。因此，很明显BST的查找效率是O(N)

另外，当BST为满二叉树/完全二叉树，BST的查找效率为O(logN)，这样的BST成为平衡搜索二叉树。

---

2. 搜索二叉树的两种模型

1）Key 模型

用途：查找某 key 值是否存在。

实际应用举例：门禁系统——读取门禁卡信息，查找该门禁卡信息是否存储在门禁系统的名单中。

上一篇中我们实现的BST即为Key模型。

2）KV 模型 （key and value）

用途：查找 key 是否存在，并通过 key 查找 value。value 是 key 的一个映射。

实际应用举例：e.g.1 英汉词典，通过查找英文找到对应的中文。e.g.2 统计出现的单词个数

实现KV模型的BST

e.g.1 英汉词典

相对于Key模型，KV模型没有很多需要更改的地方。

• 首先，每个结点多了一个key的映射值val，具体代码如下。

  template<class K, class V>
  struct BSTreeNode_KV
  {BSTreeNode_KV(const K key = K(), const V val = V()):_key(key), _val(val), _left(nullptr), _right(nullptr){}K _key;V _val;BSTreeNode_KV<K, V>* _left;BSTreeNode_KV<K, V>* _right;
  };
  

   
• insert：构造结点的时候需要多传一个参数，具体代码如下。（ps.递归版本的 find 也要相应的修改）

  bool Insert(const K& key, const V& val)
  {if (_rootp == nullptr){_rootp = new Node(key, val);return true;}Node* curp = _rootp;Node* parent_p = curp;while (curp){if (curp->_key > key){parent_p = curp;curp = curp->_left;}else if (curp->_key < key){parent_p = curp;curp = curp->_right;}elsereturn false;}Node* newp = new Node(key, val);if (parent_p->_key > key){parent_p->_left = newp;}else{parent_p->_right = newp;}return true;
  }

   
• 另外，我们可以把 find 函数修改一下，返回找到的结点的指针。具体代码如下。（ps.递归版本的 find 也要相应的修改）

  Node* Find(const K& key)
  {if (_rootp == nullptr)return nullptr;Node* curp = _rootp;while (curp){if (curp->_key > key){curp = curp->_left;}else if (curp->_key < key){curp = curp->_right;}elsereturn curp;}return nullptr;
  }
  //这里find函数没找到选择返回空指针的方式，对该情况的处理可以根据需求选择其他更合适的方式
  上面这个是类内的成员函数int main()
  {BSTree_KV<std::string, std::string> treekv;treekv.Insert("test", "测试");treekv.Insert("tress", "树");treekv.Insert("left", "左");treekv.Insert("right", "右");//…………………………………………std::string str;while (std::cin >> str)//通过这样的方式我们可以简单地实现通过英文查找中文的功能{std::cout << (treekv.Find(str))->_val << std::endl;}
  }

e.g.2 用KV模型实现统计出现次数 

示例应用代码如下。

int main
{std::vector<std::string> vs = { "what","world","speak","now","speak","now","tolerate","speak" };BSTree_KV<std::string, int> countTree;for (auto str : vs){if (countTree.Find(str) == nullptr)countTree.Insert(str, 1);else++(countTree.Find(str))->_val;}countTree.InOrder();return 0;
}

---

END