题目描述

手工课上老师拿出 N 张长方形彩纸，且每张彩纸上都画着 W*H 的网格（网格铺满整张彩纸）。现在老师将 N 张彩纸裁剪出 K 张大小相同的正方形，并且要使裁剪出的正方形的边长最大（裁剪的正方形边长必须为整数）。

例如：N = 2，有 2 张彩纸，第一张彩纸 W = 4，H = 3；第二张彩纸 W = 5，H = 4；K = 6，裁剪的 6 个正方形边长最大是 2。

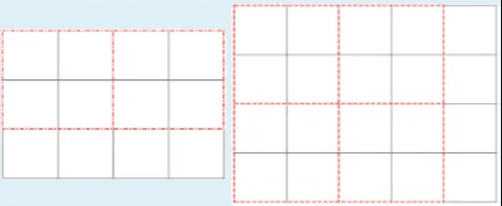
当给出 N 张长方形彩纸 W 和 H，及 K 的值，请计算出将 N 张彩纸裁剪出 K 张大小相同的正方形，正方形的边长最大是多少（裁剪的正方形边长必须为整数）。

输入格式

第一行输入两个正整数 N，K (1 < N < 100，1 < K < 100)，N 表示彩纸数量，K 表示需裁剪的正方形数量，两个正整数之间一个空格隔开；

第二行开始，输入 N 行，每行输入两个正整数 Wi，Hi (1 < Wi < 1000，1 < Hi < 1000，且 Wi ≠ Hi)，Wi表示彩纸的长度，Hi表示彩纸的宽度，两个正整数之间一个空格隔开。

输出格式

输出一个正整数，表示将 N 张彩纸裁剪出 K 张大小相同的正方形的边长最大是多少（裁剪的正方形边长必须为整数），如果不能裁剪出 K 张正方形就输出“-1”。

输入样例

输入数据 1

2 6
4 3
5 4

Copy

输出数据 1

2

AC代码 

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
 
int w[105], h[105];
 
int main()
{
  int n, k;
  cin >> n >> k;
  for (int i = 1; i <= n; i++)
    cin >> w[i] >> h[i];
 
  for (int len = 999; len >= 1; len--)
  {
    int s = 0;
    for (int i = 1; i <= n; i++)
      s += (h[i]/len) * (w[i]/len);
    if (s >= k)
    {
      cout << len << endl;
      return 0;
    }
  }
  cout << -1 << endl;
  return 0;
}