描述
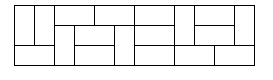
一张普通的国际象棋棋盘,它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌,每张牌恰好覆盖棋盘上相邻的两个方格,即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么,是否能够把 32 张多米诺牌摆放到棋盘上,使得任何两张多米诺牌均不重叠,每张多米诺牌覆盖两个方格,并且棋盘上所有的方格都被覆盖住?我们把这样一种排列称为棋盘被多米诺牌完美覆盖。这是一个简单的排列问题,同学们能够很快构造出许多不同的完美覆盖。但是,计算不同的完美覆盖的总数就不是一件容易的事情了。不过,同学们 发挥自己的聪明才智,还是有可能做到的。
现在我们通过计算机编程对 3 乘 n 棋盘的不同的完美覆盖的总数进行计算。
任务
对 3 乘 n 棋盘的不同的完美覆盖的总数进行计算。
输入
一次输入可能包含多行,每一行分别给出不同的 n 值 ( 即 3 乘 n 棋盘的列数 )。当输入 -1 的时候结束。
n 的值最大不超过 30.
输出
针对每一行的 n 值,输出 3 乘 n 棋盘的不同的完美覆盖的总数。
样例输入
2 8 12 -1
样例输出
3 153 2131
解题分析
首先,由于多米诺牌本身占两个格子,所以如果完全覆盖的话,那么n一个要偶数,否则3乘上一个奇数会导致格子总数为奇数,这就矛盾了。
然后,我们可以明显地感知到,我们当前排列的结果与前面的排列是有一定关系的。我们先计算一个n=2的时候,这是最小的单元(n=1的时候很明显,不可能被完全覆盖,或者从n必须为偶数理解)。我们自己脑子里摆一摆,知道n=2的时候有三种摆法。现在我们设置一个数组dp,dp[i]表示n=i时的摆法。显然,dp[i]中有一部分摆法是3*dp[i-2]。但是这显然没有包括全部的情况。那我们还漏掉了哪些情况?
简单举个例子,有两种很重要的情况被我们忽略了。比如n=4的时候,如果我们只是计算3*dp[2],那实际上我们在n=2,3这两列可以横着放多米诺牌。这部分被我们忽略了。所以我们还需要考虑dp[i-4],即我们空出四列出来,然后计算dp[i-4]*2,然后保持这两列横着放,继续i-=2,因为我们刚刚使用了dp[i-4],这是没有考虑i-4和i-5列横着放并且i-3和i-2列横着放的情况。
代码实现
#include <iostream>
using namespace std;
int dp[31]={0};int compute(int m){if(dp[m]) return dp[m];for(int i=4;i<=30;i++){dp[i]=dp[i-2]*3;for(int j=i-4;j>=0;j-=2){dp[i]+=dp[j]*2;}}return dp[m];
}int main(){int n;dp[0]=1;dp[2]=3;while(cin>>n){if(n==-1){break; }cout<<compute(n)<<endl;}return 0;
}