C++哈希
- 1.unordered_mapd
- 1.1unordered_map的构造函数
- 1.2unorder_map的容量
- 1.3unordered_map的迭代器
- 1.4unordered_map的元素访问
- 1.5unorder_map的查找
- 1.6unordered_map的修改操作
- 1.7unordered_map的桶操作
- 2.unordered_set
- 3.unordered_set和unordered_set的笔试题
- 4.哈希
- 4.1哈希概念
- 4.2哈希冲突
- 4.3哈希函数
- 4.4哈希冲突解决
- 4.4.1闭散列
- 4.4.1.1线性探测的实现
- 4.4.2开散列
- 4.4.2.1开散列的实现
- 4.unordered_map和unordered_set模拟实现
- 4.1哈希表的改造
- 4.2unordered_set模拟实现
- 4.3unordered_map模拟实现
- 5.位图
- 5.1位图的实现
- 5.2布隆过滤器
- 5.2.1布隆过滤器的实现
1.unordered_mapd
C++unorder_map官方文档
1.1unordered_map的构造函数
| 函数声明 | 功能介绍 |
|---|---|
| unordered_map | 构造不同格式的unordered_map对象 |
1.2unorder_map的容量
| 函数声明 | 功能介绍 |
|---|---|
| bool empty() const | 检测unordered_map是否为空 |
| size_t size() const | 获取unordered_map的有效元素个数 |
1.3unordered_map的迭代器
| 函数声明 | 功能介绍 |
|---|---|
| begin | 返回unordered_map第一个元素的迭代器 |
| end | 返回unordered_map最后一个元素下一个位置的迭代器 |
| cbegin | 返回unordered_map第一个元素的const迭代器 |
| cend | 返回unordered_map最后一个元素下一个位置的const迭代器 |
1.4unordered_map的元素访问
| 函数声明 | 功能介绍 |
|---|---|
| operator[] | 返回与key对应的value,没有则返回一个默认值 |
注意:
该函数中实际调用哈希桶的插入操作,用参数key与V()构造一个默认值往底层哈希桶中插入,如果key不在哈希桶中,插入成功,返回V(),插入失败,说明key已经在哈希桶中,将key对应的value返回。
1.5unorder_map的查找
| 函数声明 | 功能介绍 |
|---|---|
| iterator find(const K& key) | 返回key在哈希桶中的位置 |
| size_t count(const K& key) | 返回哈希桶中关键码为key的键值对的个数 |
注意:unordered_map中key是不能重复的,因此count函数的返回值最大为1
1.6unordered_map的修改操作
| 函数声明 | 功能介绍 |
|---|---|
| insert | 向容器中插入键值对 |
| erase | 删除容器中的键值对 |
| void clear() | 清空容器中有效元素个数 |
| void swap(unorder map&) | 交换两个容器中的元素 |
1.7unordered_map的桶操作
| 函数声明 | 功能介绍 |
|---|---|
| size_t bucket count()const | 返回哈希桶中桶的总个数 |
| size_t bucket size(size_t n)const | 返回n号桶中有效元素的总个数 |
| size_t bucket(const K& key) | 返回元素key所在的桶号 |
2.unordered_set
C++unordered_set官方文档
这里不在一 一列举
3.unordered_set和unordered_set的笔试题
在长度 2N 的数组中找出重复 N 次的元素

class Solution {
public:int repeatedNTimes(vector<int>& nums){unordered_map<int, int> found;for (int num : nums){found[num]++;}for (auto it = found.begin(); it != found.end(); ++it){if (it->second == nums.size() / 2){return it->first;}}return -1;}
};两个数组的交集

class Solution {
public:vector<int> intersection(vector<int>& nums1, vector<int>& nums2){set<int> s1(nums1.begin(),nums1.end());set<int> s2(nums2.begin(),nums2.end());auto it1=s1.begin();auto it2=s2.begin();vector<int> v;while(it1!=s1.end()&&it2!=s2.end()){if(*it1<*it2){++it1;}else if(*it1>*it2){++it2;}else{v.push_back(*it1);++it1;++it2;}}return v;}
};
两个数组的交集 II

class Solution {
public:vector<int> intersect(vector<int>& nums1, vector<int>& nums2){multiset<int> s1(nums1.begin(),nums1.end());multiset<int> s2(nums2.begin(),nums2.end());auto it1=s1.begin();auto it2=s2.begin();vector<int> v;while(it1!=s1.end()&&it2!=s2.end()){if(*it1<*it2){it1++;}else if(*it1>*it2){it2++;}else{v.push_back(*it1);it1++;it2++;}}return v;}
};
存在重复元素

class Solution {
public:bool containsDuplicate(vector<int>& nums){unordered_map<int,int> mp;for(int num:nums){mp[num]++;}auto it=mp.begin();while(it!=mp.end()){if(it->second>=2){return true;}++it;}return false;}
};
两句话中的不常见单词

class Solution {
public:vector<string> uncommonFromSentences(string s1, string s2){vector<string> v;unordered_map<string,int> mp;stringstream ss1(s1);string word;while(ss1>>word){mp[word]++;}stringstream ss2(s2);while(ss2>>word){mp[word]++;}for(auto& w:mp){if(w.second==1){v.push_back(w.first);}}return v;}
};
4.哈希
4.1哈希概念
通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一 一映射的关系,在查找时通过该函数可以很快找到该元素。
1.插入元素
根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放
2.搜索元素
对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比较,若关键码相等,则找到了
哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(Hash Table)(或者称散列表)
4.2哈希冲突
不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞。
4.3哈希函数
哈希函数设计原则:
-
1.哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1之间
-
哈希函数计算出来的地址能均匀分布在整个空间中
-
哈希函数应该比较简单
常见的哈希函数 -
直接定址法–(常用)
取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B
优点:简单、均匀
缺点:需要事先知道关键字的分布情况
使用场景:适合查找比较小且连续的情况 -
除留余数法–(常用)
设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,
按照哈希函数:Hash(key) = key% p(p<=m),将关键码转换成哈希地址
4.4哈希冲突解决
解决哈希冲突两种常见的方法是:闭散列和开散列
4.4.1闭散列
也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个” 空位置中去。
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止。
1.插入
- 通过哈希函数获取待插入元素在哈希表中的位置
- 如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突, 使用线性探测找到下一个空位置,插入新元素

2.删除
采用闭散列处理哈希冲突时,不能物理删除哈希表中已有的元素,若直接删除元素会影响其他元素的搜索。比如删除元素4,如果直接删除掉,44查找起来可能会受影响。因此线性探测采用标记的伪删除法来删除一个元素。(也就是给位置标记状态)
// 哈希表每个空间给个标记
// EMPTY此位置空, EXIST此位置已经有元素, DELETE元素已经删除
enum State{EMPTY, EXIST, DELETE};
4.4.1.1线性探测的实现
enum Status
{EMPTY,EXIST,DELETE
};template<class K,class V>
struct HashData
{pair<K, V> _kv;Status _s; //状态
};//HashFunc<int>
template<class K>
struct HashFunc
{size_t operator()(const K& Key){return (size_t)Key;}
};//HashFunc<string>
template<>
struct HashFunc<string>
{size_t operator()(const string& key){size_t hash = 0;for (auto e : key){hash *= 31;hash += e;}cout << key << ":" << hash << endl;return hash;}
};template<class K,class V,class Hash=HashFunc<K>>
class HashTable
{
public:HashTable(){_tables.resize(10);}bool Insert(const pair<K, V>& kv){if (Find(kv.first)){return false;}//负载因子0.7就扩容if (_n * 10 / _tables.size() == 7){size_t newSize = _tables.size() * 2;HashTable<K, V> newHT;newHT._tables.resize(newSize);for (size_t i = 0;i < _tables.size();i++){if (_tables[i]._s == EXIST){newHT.Insert(_tables[i]._kv);}}_tables.swap(newHT._tables);}Hash hf;size_t hashi = hf(kv.first) % _tables.size();while (_tables[hashi]._s == EXIST){hashi++;hashi %= _tables.size();}_tables[hashi]._kv = kv;_tables[hashi]._s = EXIST;++_n;return true;}HashData<K, V>* Find(const K& key){Hash hf;size_t hashi = hf(key) % _tables.size();while (_tables[hashi]._s != EMPTY){if (_tables[hashi]._s == EXIST && _tables[hashi]._kv.first == key){return &_tables[hashi];}hashi++;hashi %= _tables.size();}return nullptr;}bool Erase(const K& key){HashData<K, V>* ret = Find(key);if (ret){ret->_s = DELETE;--_n;return true;}else{return false;}}void Print(){for (size_t i = 0;i < _tables.size();i++){if (_tables[i]._s == EXIST){cout << "[" << i << "]->" << _tables[i]._kv.first << ":" << _tables[i]._kv.second << endl;}else if (_tables[i]._s == EMPTY){printf("[%d]->\n", i);}else{printf("[%d]->D\n", i);}}cout << endl;}private:vector<HashData<K,V>> _tables;size_t _n = 0;//存储的关键字的个数
};
线性探测优点:实现非常简单
线性探测缺点:一旦发生哈希冲突,所有的冲突连在一起,容易产生数据“堆积”,即:不同
关键码占据了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜索效率降
低。
4.4.2开散列
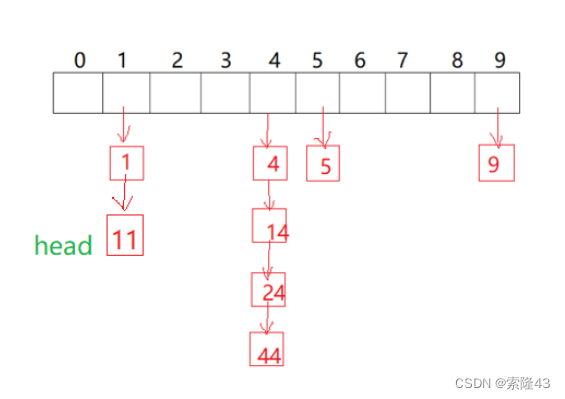
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地
址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链
接起来,各链表的头结点存储在哈希表中。
4.4.2.1开散列的实现
//HashFunc<int>
template<class K>
struct HashFunc
{size_t operator()(const K& Key){return (size_t)Key;}
};//HashFunc<string>
template<>
struct HashFunc<string>
{size_t operator()(const string& key){size_t hash = 0;for (auto e : key){hash *= 31;hash += e;}cout << key << ":" << hash << endl;return hash;}
};template<class K, class V>
struct HashNode
{HashNode* _next;pair<K, V> _kv;HashNode(const pair<K, V>& kv):_kv(kv), _next(nullptr){}
};template<class K, class V,class Hash=HashFunc<K>>
class HashTable
{typedef HashNode<K, V> Node;
public:HashTable(){_tables.resize(10);}~HashTable(){for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}}bool Insert(const pair<K, V>& kv){if (Find(kv.first))return false;Hash hf;// 负载因子最大到1if (_n == _tables.size()){vector<Node*> newTables;newTables.resize(_tables.size() * 2, nullptr);// 遍历旧表for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;//挪动到映射的新表size_t hashi = hf(cur->_kv.first) % newTables.size();cur->_next = newTables[hashi];//标记newTables[hashi] = cur;cur = next;}_tables[i] = nullptr;}_tables.swap(newTables);}size_t hashi = hf(kv.first) % _tables.size();Node* newnode = new Node(kv);// 头插newnode->_next = _tables[hashi];_tables[hashi] = newnode;++_n;return true;}Node* Find(const K& key){Hash hf;size_t hashi = hf(key) % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){return cur;}cur = cur->_next;}return nullptr;}bool Erase(const K& key){Hash hf;size_t hashi = hf(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){if (prev == nullptr){_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;return true;}prev = cur;cur = cur->_next;}return false;}void Some(){size_t bucketSize = 0;size_t maxBucketLen = 0;size_t sum = 0;double averageBucketLen = 0;for (size_t i = 0;i < _tables.size();i++){Node* cur = _tables[i];if (cur){++bucketSize;}size_t bucketLen = 0;while (cur){++bucketLen;cur = cur->_next;}sum += bucketLen;if (bucketLen > maxBucketLen){maxBucketLen = bucketLen;}}printf("all bucketSize:%d\n", _tables.size());printf("bucketSize:%d\n", bucketSize);printf("maxBucketLen:%d\n", maxBucketLen);printf("averageBucketLen:%lf\n\n", averageBucketLen);}private:vector<Node*> _tables;size_t _n = 0;
};
4.unordered_map和unordered_set模拟实现
4.1哈希表的改造
//HashFunc<int>
template<class K>
struct HashFunc
{size_t operator()(const K& Key){return (size_t)Key;}
};//HashFunc<string>
template<>
struct HashFunc<string>
{size_t operator()(const string& key){size_t hash = 0;for (auto e : key){hash *= 31;hash += e;}cout << key << ":" << hash << endl;return hash;}
};
namespace hash_bucket
{template<class T>struct HashNode{HashNode* _next;T _data;HashNode(const T& data):_data(data), _next(nullptr){}};// 前置声明template<class K, class T, class KeyOfT, class Hash>class HashTable;template<class K,class T,class Ref,class Ptr,class KeyOfT,class Hash>struct __HTIterator{typedef HashNode<T> Node;typedef __HTIterator<K, T, Ref, Ptr, KeyOfT, Hash> Self;Node* _node;const HashTable<K, T, KeyOfT, Hash>* _pht;size_t _hashi;__HTIterator(Node* node,HashTable<K,T,KeyOfT,Hash>* pht,size_t hashi):_node(node),_pht(pht),_hashi(hashi){}__HTIterator(Node* node, const HashTable<K, T, KeyOfT, Hash>* pht, size_t hashi):_node(node), _pht(pht), _hashi(hashi){}Self& operator++(){if (_node->_next){_node = _node->_next;}else{++_hashi;while (_hashi < _pht->_tables.size()){if (_pht->_tables[_hashi]){_node = _pht->_tables[_hashi];break;}++_hashi;}if (_hashi == _pht->_tables.size()){_node = nullptr;}}return *this;}Ref operator*(){return _node->_data;}Ptr operator->(){return &(_node->_data);}bool operator!=(const Self& s){return _node != s._node;}};//unordered_set->HashTable<K,K>//unordered_map->HashTable<K,pair<K,V>>template<class K, class T,class KeyOfT,class Hash>class HashTable{typedef HashNode<T> Node;template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash>friend struct __HTIterator;public:typedef __HTIterator<K, T, T&, T*, KeyOfT, Hash> iterator;typedef __HTIterator<K, T, const T&, const T*, KeyOfT, Hash> const_iterator;iterator begin(){for (size_t i = 0;i < _tables.size();i++){if (_tables[i]){return iterator(_tables[i], this, i);}}return end();}iterator end(){return iterator(nullptr, this, -1);}const_iterator begin() const{for (size_t i = 0;i < _tables.size();i++){if (_tables[i]){return const_iterator(_tables[i], this, i);}}return end();}const_iterator end() const{return const_iterator(nullptr, this, -1);}HashTable(){_tables.resize(10);}~HashTable(){for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}}pair<iterator,bool> Insert(const T& data){Hash hf;KeyOfT kot;iterator it = Find(kot(data));if (it != end()){return make_pair(it, false);}// 负载因子最大到1if (_n == _tables.size()){vector<Node*> newTables;newTables.resize(_tables.size() * 2, nullptr);// 遍历旧表for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;//挪动到映射的新表size_t hashi = hf(kot(data)) % newTables.size();cur->_next = newTables[hashi];//标记newTables[hashi] = cur;cur = next;}_tables[i] = nullptr;}_tables.swap(newTables);}size_t hashi = hf(kot(data)) % _tables.size();Node* newnode = new Node(data);// 头插newnode->_next = _tables[hashi];_tables[hashi] = newnode;++_n;return make_pair(iterator(newnode,this,hashi),true);}iterator Find(const K& key){Hash hf;KeyOfT kot;size_t hashi = hf(key) % _tables.size();Node* cur = _tables[hashi];while (cur){if (kot(cur->_data) == key){return iterator(cur,this,hashi);}cur = cur->_next;}return end();}bool Erase(const K& key){Hash hf;KeyOfT kot;size_t hashi = hf(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (kot(cur->_data) == key){if (prev == nullptr){_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;return true;}prev = cur;cur = cur->_next;}return false;}void Some(){size_t bucketSize = 0;size_t maxBucketLen = 0;size_t sum = 0;double averageBucketLen = 0;for (size_t i = 0;i < _tables.size();i++){Node* cur = _tables[i];if (cur){++bucketSize;}size_t bucketLen = 0;while (cur){++bucketLen;cur = cur->_next;}sum += bucketLen;if (bucketLen > maxBucketLen){maxBucketLen = bucketLen;}}averageBucketLen = (double)sum / (double)bucketSize;printf("all bucketSize:%d\n", _tables.size());printf("bucketSize:%d\n", bucketSize);printf("maxBucketLen:%d\n", maxBucketLen);printf("averageBucketLen:%lf\n\n", averageBucketLen);}private:vector<Node*> _tables;size_t _n = 0;};
}
4.2unordered_set模拟实现
#pragma once
#include"HashTable.h"namespace ljh
{template<class K, class Hash = HashFunc<K>>class unordered_set{struct SetKeyOfT{const K& operator()(const K& key){return key;}};public:typedef typename hash_bucket::HashTable<K, K, SetKeyOfT, Hash>::const_iterator iterator;typedef typename hash_bucket::HashTable<K, K, SetKeyOfT, Hash>::const_iterator const_iterator;/*iterator begin(){return _ht.begin();}iterator end(){return _ht.end();}*/const_iterator begin() const{return _ht.begin();}const_iterator end() const{return _ht.end();}pair<const_iterator, bool> insert(const K& key){auto ret = _ht.Insert(key);return pair<const_iterator, bool>(const_iterator(ret.first._node, ret.first._pht, ret.first._hashi), ret.second);}iterator find(const K& key){return _ht.Find(key);}bool erase(const K& key){return _ht.Erase(key);}private:hash_bucket::HashTable<K, K, SetKeyOfT, Hash> _ht;};
}
4.3unordered_map模拟实现
#pragma once
#include"HashTable.h"
namespace ljh
{template<class K,class V,class Hash=HashFunc<K>>class unordered_map{struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};public:typedef typename hash_bucket::HashTable<K, pair<const K, V>, MapKeyOfT, Hash>::iterator iterator;iterator begin(){return _ht.begin();}iterator end(){return _ht.end();}pair<iterator, bool> insert(const pair<K, V>& kv){return _ht.Insert(kv);}V& operator[](const K& key){pair<iterator, bool> ret = _ht.Insert(make_pair(key, V()));return ret.first->second;}const V& operator[](const K& key) const{pair<iterator, bool> ret = _ht.Insert(make_pair(key, V()));return ret.first->second;}iterator find(const K& key){return _ht.Find(key);}bool erase(const K& key){return _ht.Erase(key);}private:hash_bucket::HashTable<K, pair<const K, V>, MapKeyOfT, Hash> _ht;};
}
5.位图
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。
解决方案:
1:暴力遍历:时间复杂度O(N)
2.快排(O(NlogN))+二分查找(logN)
3.位图
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,可以使用一个二进制比特位来代表数据是否存在,如果二进制比特位为1,代表存在,为0代表不存在。
5.1位图的实现
//N为需要多少比特位
template<size_t N>
class bitset
{
public:bitset(){_bits.resize(N / 32 + 1);}void set(size_t x){size_t i = x / 32;size_t j = x % 32;_bits[i] |= (1 << j);}void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_bits[i] &= ~(1 << j);}bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1 << j);}private:vector<int> _bits;
};template<size_t N>
class twobitset
{
public:void set(size_t x){//00->01//01->10//10->11//11->不变if (_bs1.test(x) == false && _bs2.test(x) == false){_bs2.set(x);}else if (_bs1.test(x) == false && _bs2.test(x) == true){_bs1.set(x);_bs2.reset(x);}else if (_bs1.test(x) == true && _bs2.test(x) == false){_bs2.set(x);}}void Print(){for (size_t i = 0;i < N;i++){if (_bs1.test(i) == false && _bs2.test(i) == true){cout << "1->" << i << endl;}else if (_bs1.test(i) == true && _bs2.test(i) == false){cout << "2->" << i << endl;}}cout << endl;}private:bitset<N> _bs1;bitset<N> _bs2;
};
5.2布隆过滤器
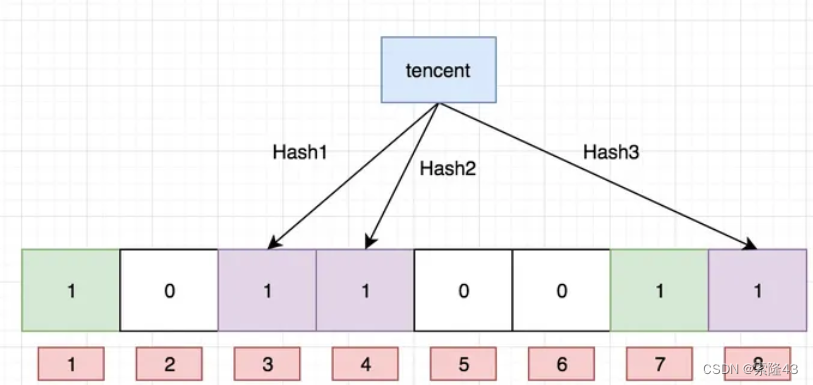
具体实现思想:用多个哈希函数,将一个数据映射到位图结构中
作用:某样东西一定不存在或者可能存在

5.2.1布隆过滤器的实现
#include<string>
#include<iostream>
#include<vector>
using namespace std;
#include"bitset.h"
struct BKDRHash
{size_t operator()(const string& key){// BKDRsize_t hash = 0;for (auto e : key){hash *= 31;hash += e;}return hash;}
};struct APHash
{size_t operator()(const string& key){size_t hash = 0;for (size_t i = 0; i < key.size(); i++){char ch = key[i];if ((i & 1) == 0){hash ^= ((hash << 7) ^ ch ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));}}return hash;}
};struct DJBHash
{size_t operator()(const string& key){size_t hash = 5381;for (auto ch : key){hash += (hash << 5) + ch;}return hash;}
};template<size_t N,class K = string,class HashFunc1 = BKDRHash,class HashFunc2 = APHash,class HashFunc3 = DJBHash>
class BloomFilter
{
public:void Set(const K& key){size_t hash1 = HashFunc1()(key) % N;size_t hash2 = HashFunc2()(key) % N;size_t hash3 = HashFunc3()(key) % N;_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);}//void Reset(const K& key);一般不支持删除bool Test(const K& key){//判断不存在是准确的,其他的都是存在偏差的size_t hash1 = HashFunc1()(key) % N;if (_bs.test(hash1) == false){return false;}size_t hash2 = HashFunc2()(key) % N;if (_bs.test(hash2) == false){return false;}size_t hash3 = HashFunc3()(key) % N;if (_bs.test(hash3) == false){return false;}// 存在误判的return true;}private:ljh::bitset<N> _bs;
};