文章目录
- HJ108 求最小公倍数
- NC95 数组中的最长连续子序列
- DP39 字母收集
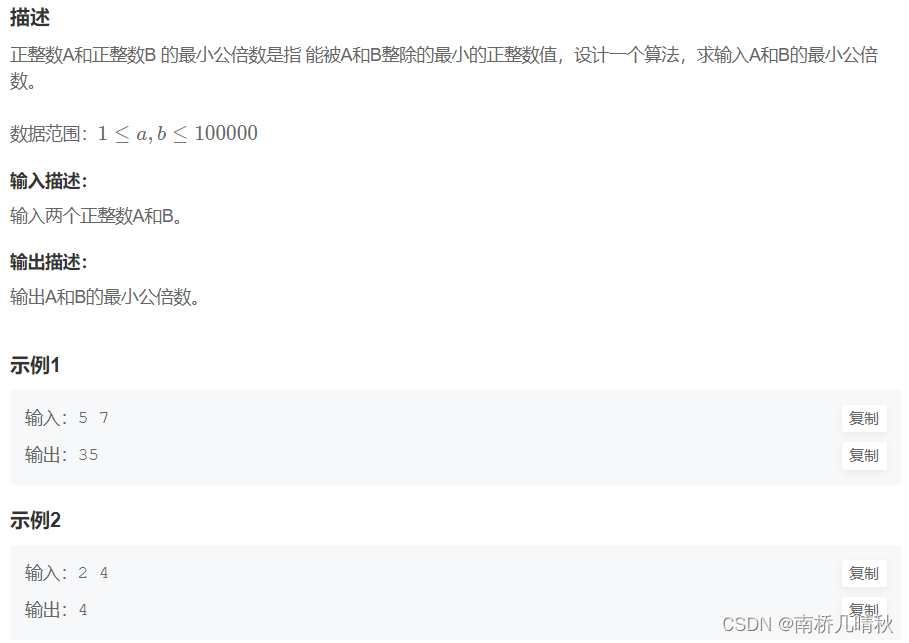
HJ108 求最小公倍数
HJ108 求最小公倍数
#include<iostream>using namespace std;int a,b;int gcd(int a,int b)
{if(b==0) return a;return gcd(b,a%b);
}
int main()
{cin>>a>>b;int t=gcd(a,b);int ans=a*b/t;cout<<ans<<endl;return 0;
}
NC95 数组中的最长连续子序列
NC95 数组中的最长连续子序列

class Solution {
public:int MLS(vector<int>& arr) {int n=arr.size();sort(arr.begin(),arr.end());int ans=0;for(int i=0;i<n;){int j=i+1,cnt=1;while(j<n){if(arr[j]-arr[j-1]==1){cnt++;j++;}else if(arr[j]-arr[j-1]==0) j++;else break;}ans=max(cnt,ans);i=j;}return ans;}
};
DP39 字母收集
DP39 字母收集

#include<iostream>using namespace std;const int N=505;
int m,n;
char g[N][N];
int dp[N][N];int main()
{cin>>m>>n;for(int i=0;i<m;i++){for(int j=0;j<n;j++){cin>>g[i][j];}}for(int i=0;i<=m;i++){for(int j=0;j<=n;j++){int t=0;if(g[i][j]=='l') t=4;else if(g[i][j]=='o') t=3;else if(g[i][j]=='v') t=2;else if(g[i][j]=='e') t=1;dp[i][j]=max(dp[i][j-1],dp[i-1][j])+t;}}cout<<dp[m][n]<<endl;return 0;
}