🍄题目描述
为了配平一个化学方程式,我们可以令方程式中各物质的系数为未知数,然后针对涉及的每一种元素,列出关于系数的方程,形成一个齐次线性方程组。然后求解这个方程组,得到各物质的系数。这样,我们就把化学方程式配平的问题,转化为了求解齐次线性方程组的问题。 如果方程组没有非零解,那么这个方程式是不可以配平的。反之,如果方程组有非零解,我们就可能得到一个配平的方程式。当然,最终得到的方程式仍然需要结合化学知识进行检验,对此我们不再进一步考虑,仅考虑非零解的存在。
例如要配平化学方程式:Al2(SO4)3+NH3⋅H2O→Al(OH)3+(NH4)2SO4Al2(SO4)3+NH3⋅H2O→Al(OH)3+(NH4)2SO4
首先假定所有物质在方程的同一侧,即不考虑哪个是反应物,哪个是生成物,分别设这些物质的系数为 𝑥1,𝑥2,𝑥3,𝑥4x1,x2,x3,x4,则可以针对出现的各个元素,列出如下的方程组:
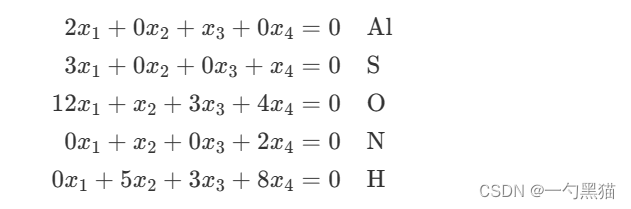
用矩阵的形式表示为:
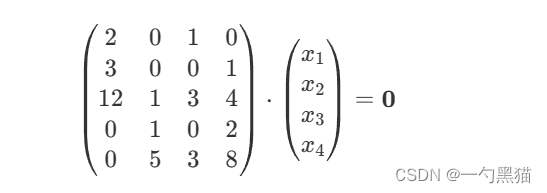
对系数矩阵实施高斯消元,得到系数矩阵的一个行阶梯形式:
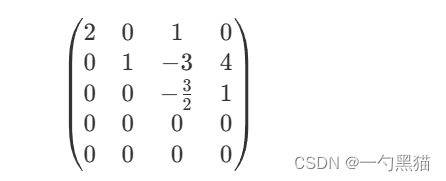
由此可见,系数矩阵的秩为 3。根据线性代数的知识,我们知道,齐次线性方程组 𝐴𝑋=0AX=0 的解空间的维数等于其未知数个数减去系数矩阵的秩 rank𝐴rankA。而要让方程式配平,即要求方程组存在非零解, 那么就需要让解空间的维数大于 00,即系数矩阵的秩小于未知数个数。因此,我们可以通过判断系数矩阵的秩是否小于未知数个数,来判断方程式是否可以配平。如果可以配平,则可以通过解的符号来判断反应物和生成物的位置。
本题中,我们将给出一些化学方程式,请你按照上述方法判断它们是否可以配平。为了便于程序处理,我们用到的化学式,会被化简为只包含小写字母和数字的字符串,不包含括号。 其中连续的字母表示一种元素,随后的数字表示原子个数。原子个数为 1 时不省略数字;一个化学式中包含的元素不重复。例如,上述方程式中的化学式可以化简为 al2s3o12、n1h5o1、al1o3h3、n2h8s1o4。
输入格式
从标准输入读入数据。
输入的第一行包含一个正整数 𝑛n,表示需要判断的化学方程式的个数。
接下来的 𝑛n 行,每行描述了一个需要被配平的化学方程式。包含空格分隔的一个正整数和全部涉及物质的化学式。其中,正整数 𝑚m 表示方程式中的物质;随后的 𝑚m 个字符串,依次给出方程式中的反应物的化学式和生成物的化学式。
输出格式
输出到标准输出。
输出包含 𝑛n 行,每行包含字母 Y 或 N,表示按题设方法,所给待配平化学方程式能否配平。
🍄AC代码
#include<bits/stdc++.h>
using namespace std;//统计某物质中的全部元素个数
map<string,int> analyse(string s){map<string,int> mmap;string element="";string number="";int flag=0; // 0表示元素,1表示元素个数for(int i=0;i<s.length();i++){if(!(s[i]>='0'&&s[i]<='9')){//字母if(flag==1){//从数字转为字母,说明循环到新的元素了,需要把上一个元素的数量放入mapflag=0;//此时element和number都表示上一个元素的,放入map后需清空mmap[element]=stoi(number);element="";number="";}element+=s[i];}else{//数字if(flag==0){flag=1;}number+=s[i];}}mmap[element]=stoi(number);return mmap;
}//计算矩阵的秩
int compute_zhi(vector<vector<double>> matrix){int m=matrix.size(),n=matrix[0].size();for(int pos=0;pos<n;pos++){if(matrix[pos][pos]==0){//在剩余行中找到第一列数字不为0的行与当前行交换int flag=0;for(int i=pos+1;i<m;i++){if(matrix[i][pos]!=0){flag=1;swap(matrix[i],matrix[pos]);}}if(!flag) continue; //如果其余行的第一列都为0,则跳过本轮循环}for(int i=pos+1;i<m;i++){double t=matrix[i][pos]/matrix[pos][pos]; if(t==0) continue; //倍数为0,整行元素不变,跳过for(int j=pos;j<m;j++)matrix[i][j]=matrix[i][j]-matrix[pos][j]*t;}}//对最后一列元素从倒数第一行遍历,统计为0的行数,矩阵的秩=总行数-0的行数int cnt=0,p=m-1;while(matrix[p--][n-1]==0) cnt++;return m-cnt;}//判断化学方程式否能配平
void judge(int n){string s;vector<map<string,int>> v; //记录每个物质中的元素个数map<string,int> ele_sort; //记录元素在矩阵中的行下标int cur_sort=0; //当前元素行下标for(int i=0;i<n;i++){cin>>s;//统计物质中每个元素的个数map<string,int> mmap=analyse(s);v.push_back(mmap);for(auto it=mmap.begin();it!=mmap.end();it++){//如果物质中的某元素还未出现过,则放入元素集合中if(ele_sort.find(it->first)==ele_sort.end()){ele_sort[it->first]=cur_sort++;}}}//生成二维矩阵vector<vector<double>> matrix(ele_sort.size(),vector<double>(n));for(int i=0;i<n;i++){for(auto it=v[i].begin();it!=v[i].end();it++)matrix[ele_sort[it->first]][i]=it->second;}if(matrix.size()<n){//如果元素个数小于物质个数,一定能配平cout<<"Y"<<endl;}else{//计算矩阵的秩并判断int r=compute_zhi(matrix);if(r<n) cout<<"Y"<<endl;else cout<<"N"<<endl;}}int main(){int n,m;cin>>n;for(int i=0;i<n;i++){int m;cin>>m;judge(m);}return 0;
}