数据结构之二叉树详解[1]-编程知识

在前面我们介绍了堆和二叉树的基本概念后，本篇文章将带领大家深入学习链式二叉树。

1.预备知识

2.二叉树结点的创建

3.二叉树的遍历

3.1前序遍历

3.2中序遍历

3.3 后序遍历

4.统计二叉树的结点个数

5.二叉树叶子结点的个数

6.二叉树第k层的结点个数

7.总结

1.预备知识

由于二叉树的性质，我们在实现二叉树及其相关功能时会经常使用到递归的操作。

所以我们首先介绍一下递归算法。

在百度百科中，对于递归算法的定义是：某个函数直接或者间接地调用自身，这样原问题的求解就转换为了许多性质相同但是规模更小的子问题。

很多同学或许对这句话无法理解，没有关系。

在这里我们仅仅将其当作一个工具，在编写代码时，我们只需搞清楚繁杂的递归调用中的一次调用即可，不需要去深究他调用的过程。在文章后续的代码实现中，大家可以深刻体会到这句话的意思。

2.二叉树结点的创建

既然是链式二叉树，对学习过链表的大家就很简单了。直接上代码

typedef char BTDataType;typedef struct BTreeNode//每一个结点的结构
{BTreeNode* left;//指向左树BTreeNode* right; //指向右树BTDataType data;//结点的值
}BTNode;BTNode* BuyNode(BTDataType x)//为新结点开辟空间
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}

3.二叉树的遍历

二叉树的遍历有四种：前序遍历、中序遍历、后序遍历、层序遍历。

今天我们在这里讲解前三种遍历，层序遍历请看下回分解。

3.1前序遍历

前序遍历就是先遍历根结点，在遍历左子树，最后遍历右子树。

理解了概念我们直接上代码。

void PreOrder(BTNode* root)//前序 根 左子树 右子树
{if (root == NULL){printf("NULL");return;}else {printf("%c", root->data);//打印根节点PreOrder(root->left);//递归遍历左子树PreOrder(root->right);//递归遍历右子树}
}

这里我们就使用到了递归。该如何理解呢。

我们只关注一次调用，既然遍历左树，

那么我们就让根去找，即 PreOrder(root->left)。

遍历右树，即PreOrder(root->right)。

中间是如何进行调用的细节我们不需要深究，我们只需要知道这个递归的写法。剩下的交给计算机。如果大家仍没理解，可以画个对照代码画一个草图。

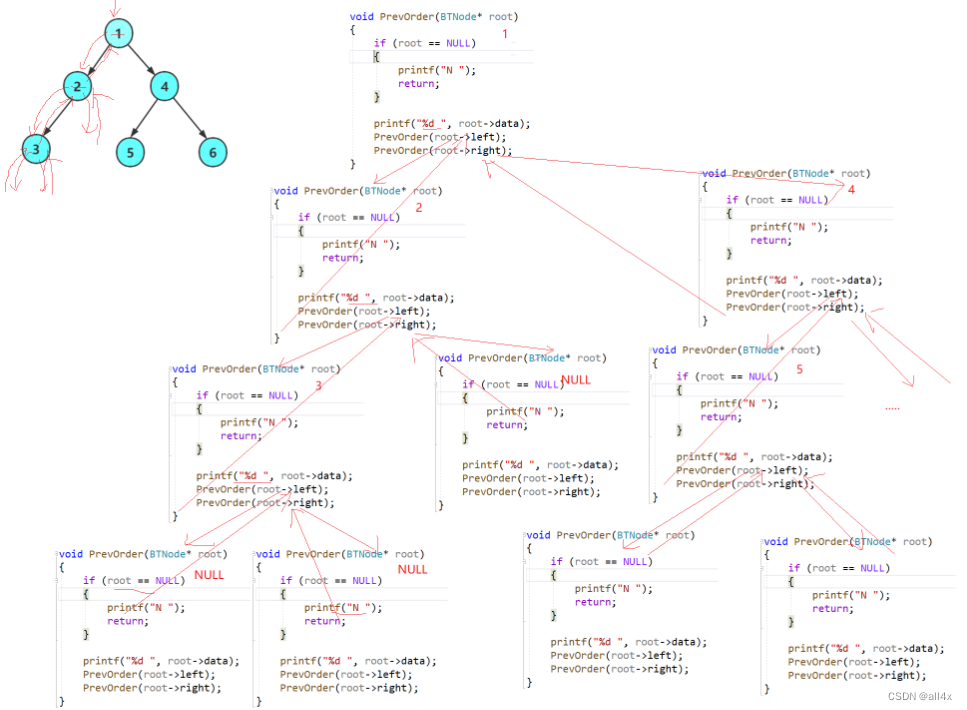
3.2中序遍历

中序遍历：先遍历左子树，在找根，最后遍历右子树。

代码如下

void InOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}else {InOrder(root->left);//遍历左树printf("%c", root->data);//找根InOrder(root->right);//遍历右树}
}

这里的递归我们仍然按一样的方法进行理解，只看一层调用。大家可以看图理解。

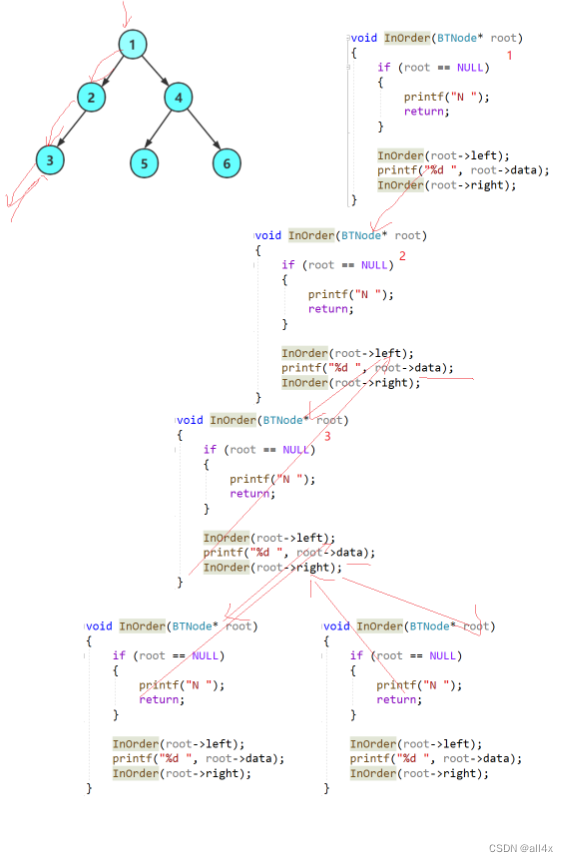
3.3 后序遍历

后序遍历：先遍历左子树，再遍历右子树，最后找根。

void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}else {PostOrder(root->left);//遍历左树PostOrder(root->right);//遍历右树printf("%c", root->data);//找根}
}

后序的图大家就自己画画吧。

4.统计二叉树的结点个数

如何统计二叉树的结点个数呢。

思路很简单，没遍历一个非空结点，个数加一。我们看下面代码。

void TreeSize(BTNode* root)
{if (root == NULL)return;int count = 0;count++;//既然不为空，那么一定就有一个结点的存在TreeSize(root->left);TreeSize(root->right);
}

如果大家觉得这个代码对的话，那就掉入陷阱了！

在递归调用中，count存在于栈帧之中，并且递归的每一次调用都会开辟新的一块栈帧，这样的话我们的count就无法进行值的保存而达到连续的效果。所以这里我们不能这样进行实现。

下面我们介绍正确的写法。

void TreeSize(BTNode* root,int*p)//p为指向节点个数的指针
{if (root == NULL)return;++(*p);//结点个数++，既然不为空，那么一定有一个根结点，所以先++TreeSize(root->left, p);//遍历左子树的结点TreeSize(root->right, p);//遍历右子树的结点
}

我们在这里运用定义了一个外部指针变量，用来记录结点的个数，传入的是记录结点个数变量的地址。这样就可以避免原来出现的问题了。

其实这里还有个更加简单的方法，直接用root来记录结点个数。

int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

5.二叉树叶子结点的个数

既然可以得到结点总数，那叶子结点是不是也可以得到呢。我们先上代码再解释。

int BTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL) //叶子结点的特点{return 1;}return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);//找叶子结点
}

既然要找叶子结点首先我们要知道叶子结点的性质：左右子树均为空。

所以我们在递归的时候需要加入叶子结点的判断条件，如果是叶子结点就要返回。

当然在进行递归前要判断根节点是否存在或者根结点是否有值，我们将其划分为代码中的一中情况。

6.二叉树第k层的结点个数

我们该如何求任意一层的结点个数呢。

我们将求第k层的结点个数转化为求第k-1层结点的左右子树个树是不是就和我们求叶子结点个数大同小异了呢！

int BTreeLayerSize(BTNode* root,int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BTreeLayerSize(root->left, k - 1) + BTreeLayerSize(root->right, k - 1);
}

我们加入需要的层数k，我们从根结点往下找第k层，如果要使其找到k层，就要使k=1。我们画图理解。