目录
- 一、引言
- 二、实例介绍
- 1.百分位数为横条形图
- 2.箱线图定制化
- 3.带有自定义填充颜色的箱线图
- 4.箱线图
- 5.箱线图和小提琴图
- 6.二维数据集的置信椭圆
一、引言
matplotlib库 可以用来创建各种静态、动态、交互式的图形,并广泛应用于数据分析和数据可视化领域。
二、实例介绍
1.百分位数为横条形图
2.箱线图定制化
3.带有自定义填充颜色的箱线图
4.箱线图
5.箱线图和小提琴图
6.二维数据集的置信椭圆
1.百分位数为横条形图
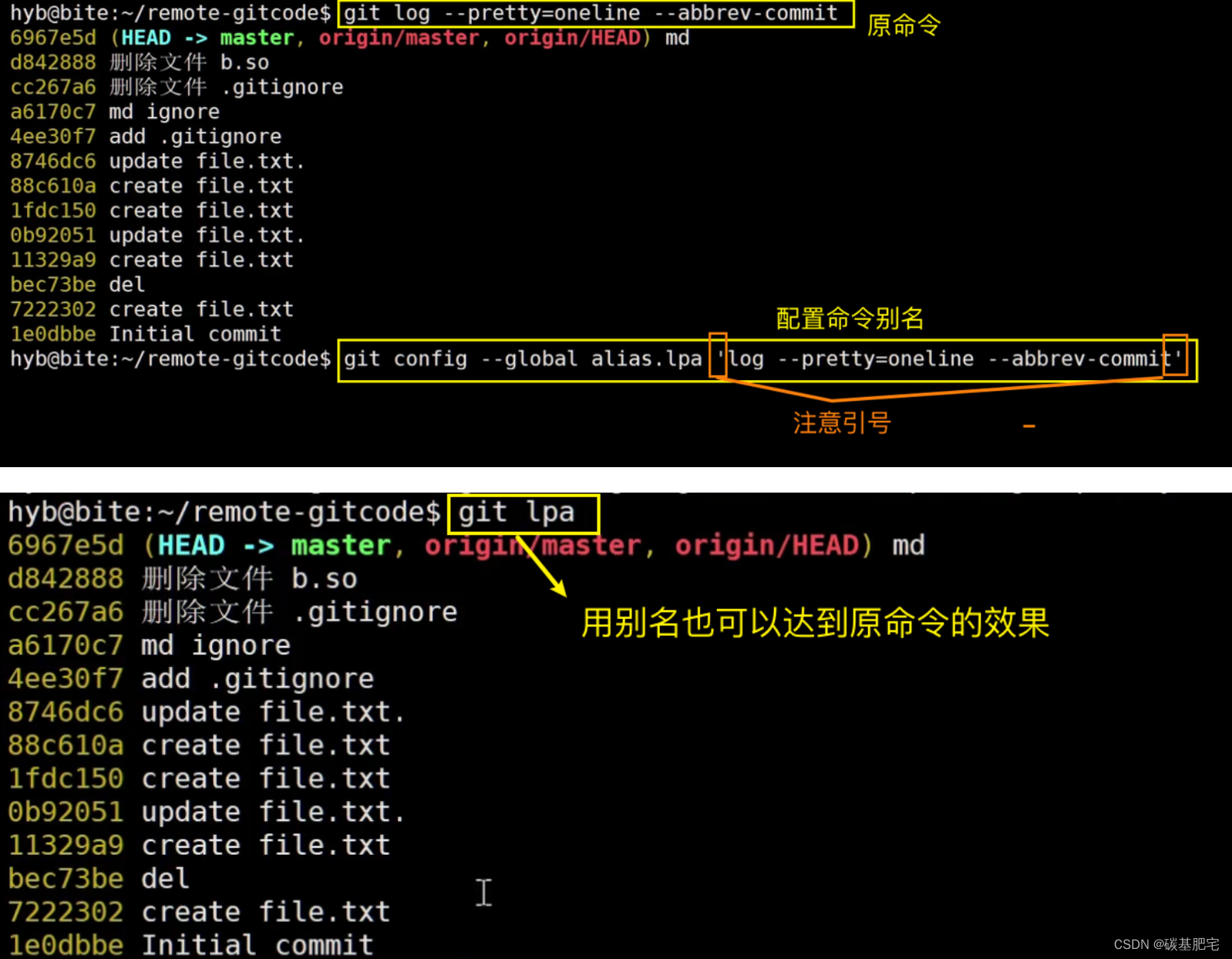
条形图对于可视化计数或带有误差条的汇总统计数据很有用。本例来自一个应用程序,在这个应用程序中,小学体育老师希望能够向家长展示他们的孩子在一些健身测试中的表现。绘图代码如下:
from collections import namedtupleimport matplotlib.pyplot as plt
import numpy as npStudent = namedtuple('Student', ['name', 'grade', 'gender'])
Score = namedtuple('Score', ['value', 'unit', 'percentile'])def to_ordinal(num):"""Convert an integer to an ordinal string, e.g. 2 -> '2nd'."""suffixes = {str(i): vfor i, v in enumerate(['th', 'st', 'nd', 'rd', 'th','th', 'th', 'th', 'th', 'th'])}v = str(num)# special case early teensif v in {'11', '12', '13'}:return v + 'th'return v + suffixes[v[-1]]def format_score(score):"""Create score labels for the right y-axis as the test name followed by themeasurement unit (if any), split over two lines."""return f'{score.value}\n{score.unit}' if score.unit else str(score.value)def plot_student_results(student, scores_by_test, cohort_size):fig, ax1 = plt.subplots(figsize=(9, 7), layout='constrained')fig.canvas.manager.set_window_title('Eldorado K-8 Fitness Chart')ax1.set_title(student.name)ax1.set_xlabel('Percentile Ranking Across {grade} Grade {gender}s\n''Cohort Size: {cohort_size}'.format(grade=to_ordinal(student.grade),gender=student.gender.title(),cohort_size=cohort_size))test_names = list(scores_by_test.keys())percentiles = [score.percentile for score in scores_by_test.values()]rects = ax1.barh(test_names, percentiles, align='center', height=0.5)# Partition the percentile values to be able to draw large numbers in# white within the bar, and small numbers in black outside the bar.large_percentiles = [to_ordinal(p) if p > 40 else '' for p in percentiles]small_percentiles = [to_ordinal(p) if p <= 40 else '' for p in percentiles]ax1.bar_label(rects, small_percentiles,padding=5, color='black', fontweight='bold')ax1.bar_label(rects, large_percentiles,padding=-32, color='white', fontweight='bold')ax1.set_xlim([0, 100])ax1.set_xticks([0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100])ax1.xaxis.grid(True, linestyle='--', which='major',color='grey', alpha=.25)ax1.axvline(50, color='grey', alpha=0.25) # median position# Set the right-hand Y-axis ticks and labelsax2 = ax1.twinx()# Set equal limits on both yaxis so that the ticks line upax2.set_ylim(ax1.get_ylim())# Set the tick locations and labelsax2.set_yticks(np.arange(len(scores_by_test)),labels=[format_score(score) for score in scores_by_test.values()])ax2.set_ylabel('Test Scores')student = Student(name='Johnny Doe', grade=2, gender='Boy')
scores_by_test = {'Pacer Test': Score(7, 'laps', percentile=37),'Flexed Arm\n Hang': Score(48, 'sec', percentile=95),'Mile Run': Score('12:52', 'min:sec', percentile=73),'Agility': Score(17, 'sec', percentile=60),'Push Ups': Score(14, '', percentile=16),
}plot_student_results(student, scores_by_test, cohort_size=62)
plt.show()
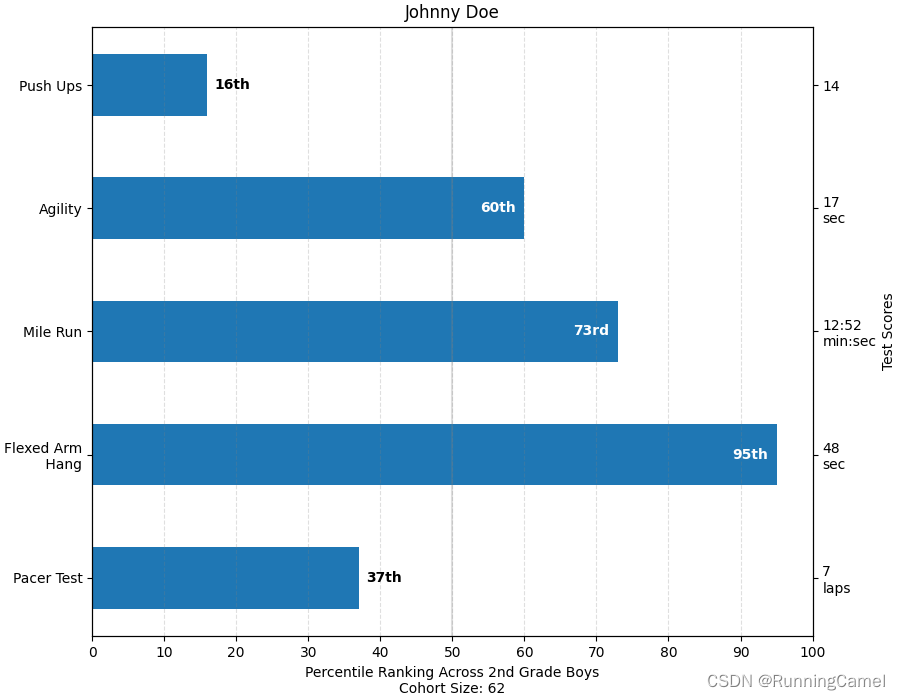
2.箱线图定制化
这个示例演示了如何使用各种关键字参数来完全自定义框图。第一个图演示了如何删除和添加单个组件(注意,平均值是默认情况下唯一未显示的值)。第二张图展示了如何定制艺术家的风格。它还演示了如何将晶须的限制设置为特定的百分位数(右下轴)。关于箱形图及其历史的一个很好的一般参考资料可以在这里找到: https://vita.had.co.nz/papers/boxplots.pdf
import matplotlib.pyplot as plt
import numpy as np# fake data
np.random.seed(19680801)
data = np.random.lognormal(size=(37, 4), mean=1.5, sigma=1.75)
labels = list('ABCD')
fs = 10 # fontsize
fig, axs = plt.subplots(nrows=2, ncols=3, figsize=(6, 6), sharey=True)
axs[0, 0].boxplot(data, labels=labels)
axs[0, 0].set_title('Default', fontsize=fs)axs[0, 1].boxplot(data, labels=labels, showmeans=True)
axs[0, 1].set_title('showmeans=True', fontsize=fs)axs[0, 2].boxplot(data, labels=labels, showmeans=True, meanline=True)
axs[0, 2].set_title('showmeans=True,\nmeanline=True', fontsize=fs)axs[1, 0].boxplot(data, labels=labels, showbox=False, showcaps=False)
tufte_title = 'Tufte Style \n(showbox=False,\nshowcaps=False)'
axs[1, 0].set_title(tufte_title, fontsize=fs)axs[1, 1].boxplot(data, labels=labels, notch=True, bootstrap=10000)
axs[1, 1].set_title('notch=True,\nbootstrap=10000', fontsize=fs)axs[1, 2].boxplot(data, labels=labels, showfliers=False)
axs[1, 2].set_title('showfliers=False', fontsize=fs)for ax in axs.flat:ax.set_yscale('log')ax.set_yticklabels([])fig.subplots_adjust(hspace=0.4)
plt.show()
结果如下图所示,演示如何切换不同元素的显示:
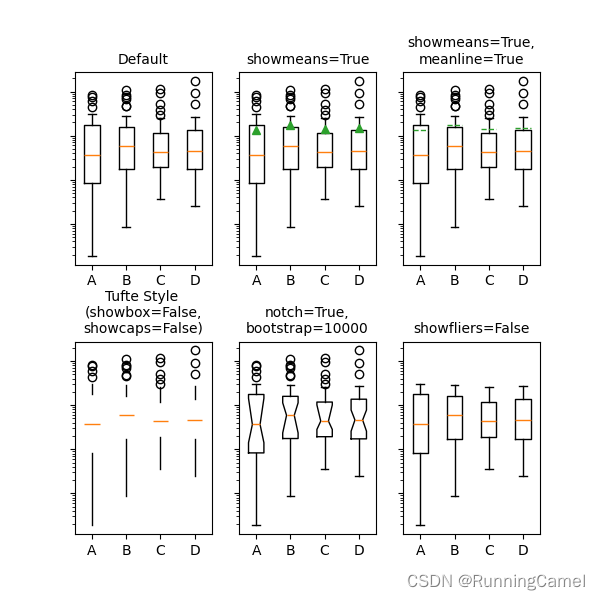
演示如何自定义显示不同的元素:
import matplotlib.pyplot as plt
import numpy as np# fake data
np.random.seed(19680801)
data = np.random.lognormal(size=(37, 4), mean=1.5, sigma=1.75)
labels = list('ABCD')
fs = 10 # fontsizeboxprops = dict(linestyle='--', linewidth=3, color='darkgoldenrod')
flierprops = dict(marker='o', markerfacecolor='green', markersize=12,markeredgecolor='none')
medianprops = dict(linestyle='-.', linewidth=2.5, color='firebrick')
meanpointprops = dict(marker='D', markeredgecolor='black',markerfacecolor='firebrick')
meanlineprops = dict(linestyle='--', linewidth=2.5, color='purple')fig, axs = plt.subplots(nrows=2, ncols=3, figsize=(6, 6), sharey=True)
axs[0, 0].boxplot(data, boxprops=boxprops)
axs[0, 0].set_title('Custom boxprops', fontsize=fs)axs[0, 1].boxplot(data, flierprops=flierprops, medianprops=medianprops)
axs[0, 1].set_title('Custom medianprops\nand flierprops', fontsize=fs)axs[0, 2].boxplot(data, whis=(0, 100))
axs[0, 2].set_title('whis=(0, 100)', fontsize=fs)axs[1, 0].boxplot(data, meanprops=meanpointprops, meanline=False,showmeans=True)
axs[1, 0].set_title('Custom mean\nas point', fontsize=fs)axs[1, 1].boxplot(data, meanprops=meanlineprops, meanline=True,showmeans=True)
axs[1, 1].set_title('Custom mean\nas line', fontsize=fs)axs[1, 2].boxplot(data, whis=[15, 85])
axs[1, 2].set_title('whis=[15, 85]\n#percentiles', fontsize=fs)for ax in axs.flat:ax.set_yscale('log')ax.set_yticklabels([])fig.suptitle("I never said they'd be pretty")
fig.subplots_adjust(hspace=0.4)
plt.show()
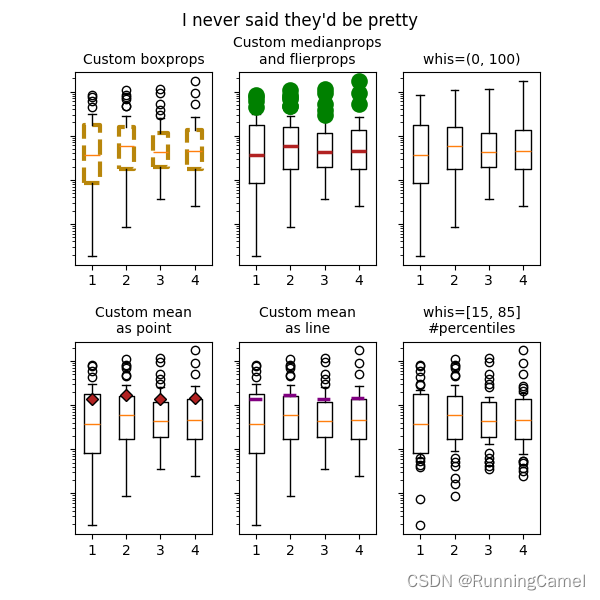
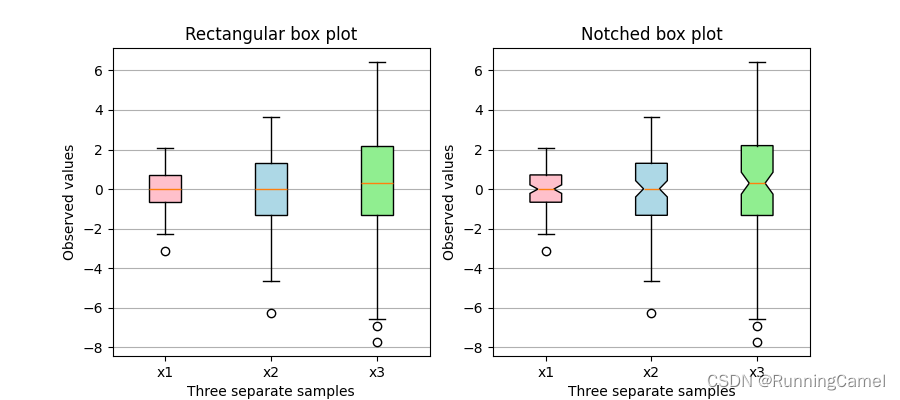
3.带有自定义填充颜色的箱线图
该图说明了如何创建两种类型的框图(矩形和缺口),以及如何通过访问框图的艺术家的属性来使用自定义颜色填充它们。此外,labels参数用于为每个样本提供x-tick标签。
import matplotlib.pyplot as plt
import numpy as np# Random test data
np.random.seed(19680801)
all_data = [np.random.normal(0, std, size=100) for std in range(1, 4)]
labels = ['x1', 'x2', 'x3']fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(9, 4))# rectangular box plot
bplot1 = ax1.boxplot(all_data,vert=True, # vertical box alignmentpatch_artist=True, # fill with colorlabels=labels) # will be used to label x-ticks
ax1.set_title('Rectangular box plot')# notch shape box plot
bplot2 = ax2.boxplot(all_data,notch=True, # notch shapevert=True, # vertical box alignmentpatch_artist=True, # fill with colorlabels=labels) # will be used to label x-ticks
ax2.set_title('Notched box plot')# fill with colors
colors = ['pink', 'lightblue', 'lightgreen']
for bplot in (bplot1, bplot2):for patch, color in zip(bplot['boxes'], colors):patch.set_facecolor(color)# adding horizontal grid lines
for ax in [ax1, ax2]:ax.yaxis.grid(True)ax.set_xlabel('Three separate samples')ax.set_ylabel('Observed values')plt.show()
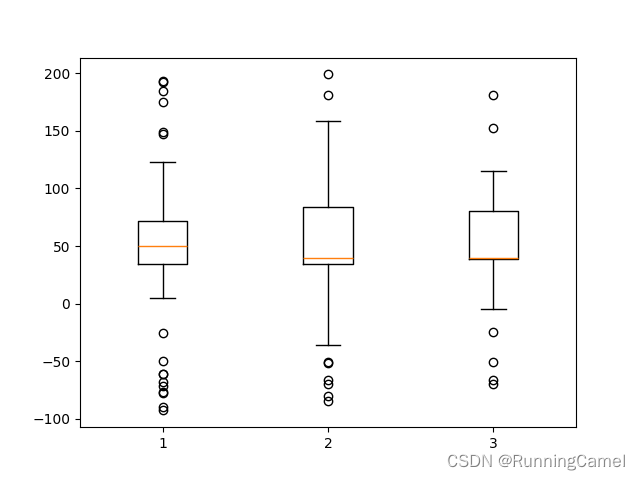
4.箱线图
使用matplotlib可视化箱线图。
下面的示例展示了如何使用Matplotlib可视化箱线图。有许多选项可以控制它们的外观和用于汇总数据的统计信息。
import matplotlib.pyplot as plt
import numpy as npfrom matplotlib.patches import Polygon# Fixing random state for reproducibility
np.random.seed(19680801)# fake up some data
spread = np.random.rand(50) * 100
center = np.ones(25) * 50
flier_high = np.random.rand(10) * 100 + 100
flier_low = np.random.rand(10) * -100
data = np.concatenate((spread, center, flier_high, flier_low))fig, axs = plt.subplots(2, 3)# basic plot
axs[0, 0].boxplot(data)
axs[0, 0].set_title('basic plot')# notched plot
axs[0, 1].boxplot(data, 1)
axs[0, 1].set_title('notched plot')# change outlier point symbols
axs[0, 2].boxplot(data, 0, 'gD')
axs[0, 2].set_title('change outlier\npoint symbols')# don't show outlier points
axs[1, 0].boxplot(data, 0, '')
axs[1, 0].set_title("don't show\noutlier points")# horizontal boxes
axs[1, 1].boxplot(data, 0, 'rs', 0)
axs[1, 1].set_title('horizontal boxes')# change whisker length
axs[1, 2].boxplot(data, 0, 'rs', 0, 0.75)
axs[1, 2].set_title('change whisker length')fig.subplots_adjust(left=0.08, right=0.98, bottom=0.05, top=0.9,hspace=0.4, wspace=0.3)# fake up some more data
spread = np.random.rand(50) * 100
center = np.ones(25) * 40
flier_high = np.random.rand(10) * 100 + 100
flier_low = np.random.rand(10) * -100
d2 = np.concatenate((spread, center, flier_high, flier_low))
# Making a 2-D array only works if all the columns are the
# same length. If they are not, then use a list instead.
# This is actually more efficient because boxplot converts
# a 2-D array into a list of vectors internally anyway.
data = [data, d2, d2[::2]]# Multiple box plots on one Axes
fig, ax = plt.subplots()
ax.boxplot(data)plt.show()
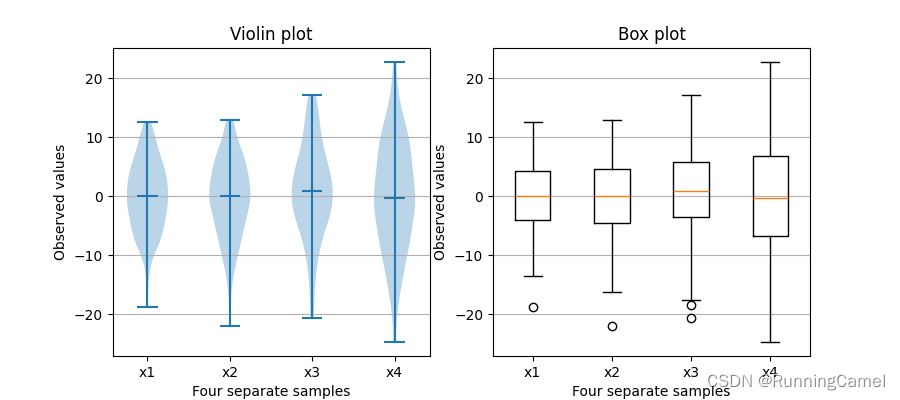
5.箱线图和小提琴图
小提琴图与箱形图密切相关,它们都添加了有用的信息,如样本数据的分布(密度迹)。默认情况下,箱形图显示1.5 *四分位数范围以外的数据点,小提琴图要求matplotlib >= 1.4。
import matplotlib.pyplot as plt
import numpy as npfig, axs = plt.subplots(nrows=1, ncols=2, figsize=(9, 4))# Fixing random state for reproducibility
np.random.seed(19680801)# generate some random test data
all_data = [np.random.normal(0, std, 100) for std in range(6, 10)]# plot violin plot
axs[0].violinplot(all_data,showmeans=False,showmedians=True)
axs[0].set_title('Violin plot')# plot box plot
axs[1].boxplot(all_data)
axs[1].set_title('Box plot')# adding horizontal grid lines
for ax in axs:ax.yaxis.grid(True)ax.set_xticks([y + 1 for y in range(len(all_data))],labels=['x1', 'x2', 'x3', 'x4'])ax.set_xlabel('Four separate samples')ax.set_ylabel('Observed values')plt.show()
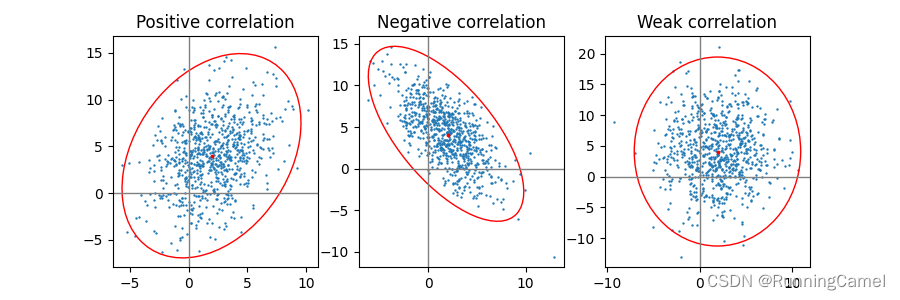
6.二维数据集的置信椭圆
如何使用pearson相关系数绘制二维数据集的置信椭圆。这里解释并证明了用来获得正确几何图形的方法 https://carstenschelp.github.io/2018/09/14/Plot_Confidence_Ellipse_001.html.
该方法避免了使用迭代特征分解算法,并利用了归一化协方差矩阵(由pearson相关系数和1组成)特别易于处理的事实。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse
import matplotlib.transforms as transforms
绘图函数本身
这个函数绘制给定的类数组变量x和y的协方差的置信椭圆。椭圆被绘制到给定的轴-对象ax中。
椭圆的半径可以通过n_std来控制,这是标准偏差的数量。默认值为3,如果数据像这些示例中一样呈正态分布,则椭圆将包含98.9%的点(1-D中的3个标准差包含99.7%的数据,这是2-D中的98.9%的数据)。
def confidence_ellipse(x, y, ax, n_std=3.0, facecolor='none', **kwargs):"""Create a plot of the covariance confidence ellipse of *x* and *y*.Parameters----------x, y : array-like, shape (n, )Input data.ax : matplotlib.axes.AxesThe axes object to draw the ellipse into.n_std : floatThe number of standard deviations to determine the ellipse's radiuses.**kwargsForwarded to `~matplotlib.patches.Ellipse`Returns-------matplotlib.patches.Ellipse"""if x.size != y.size:raise ValueError("x and y must be the same size")cov = np.cov(x, y)pearson = cov[0, 1]/np.sqrt(cov[0, 0] * cov[1, 1])# Using a special case to obtain the eigenvalues of this# two-dimensional dataset.ell_radius_x = np.sqrt(1 + pearson)ell_radius_y = np.sqrt(1 - pearson)ellipse = Ellipse((0, 0), width=ell_radius_x * 2, height=ell_radius_y * 2,facecolor=facecolor, **kwargs)# Calculating the standard deviation of x from# the squareroot of the variance and multiplying# with the given number of standard deviations.scale_x = np.sqrt(cov[0, 0]) * n_stdmean_x = np.mean(x)# calculating the standard deviation of y ...scale_y = np.sqrt(cov[1, 1]) * n_stdmean_y = np.mean(y)transf = transforms.Affine2D() \.rotate_deg(45) \.scale(scale_x, scale_y) \.translate(mean_x, mean_y)ellipse.set_transform(transf + ax.transData)return ax.add_patch(ellipse)
创建相关数据集的辅助函数
创建具有指定二维平均值(mu)和维度(scale)的随机二维数据集。相关性可以通过参数“依赖性”(一个2x2矩阵)来控制。
def get_correlated_dataset(n, dependency, mu, scale):latent = np.random.randn(n, 2)dependent = latent.dot(dependency)scaled = dependent * scalescaled_with_offset = scaled + mu# return x and y of the new, correlated datasetreturn scaled_with_offset[:, 0], scaled_with_offset[:, 1]
正、负、弱相关
请注意,弱相关性的形状(右)是椭圆形,而不是圆形,因为x和y的比例不同。然而,x和y不相关的事实是,椭圆的轴线与坐标系的x轴和y轴对齐。
np.random.seed(0)PARAMETERS = {'Positive correlation': [[0.85, 0.35],[0.15, -0.65]],'Negative correlation': [[0.9, -0.4],[0.1, -0.6]],'Weak correlation': [[1, 0],[0, 1]],
}mu = 2, 4
scale = 3, 5fig, axs = plt.subplots(1, 3, figsize=(9, 3))
for ax, (title, dependency) in zip(axs, PARAMETERS.items()):x, y = get_correlated_dataset(800, dependency, mu, scale)ax.scatter(x, y, s=0.5)ax.axvline(c='grey', lw=1)ax.axhline(c='grey', lw=1)confidence_ellipse(x, y, ax, edgecolor='red')ax.scatter(mu[0], mu[1], c='red', s=3)ax.set_title(title)plt.show()
完整代码运行之后,图形显示如下:
E N D ! \color{#4285f4}{\mathbf{E}}\color{#ea4335}{\mathbf{N}}\color{#fbbc05}{\mathbf{D}}\color{#4285f4}{\mathbf{!}} END!