比赛链接
这场不难, G G G 和 H H H 比较有意思。 G G G 题需要一定的二进制和数据结构的知识, H H H 题是个 2 − s a t 2-sat 2−sat 的题,算法名字吓人但是其实很简单,题目本身也很板,建议趁机学习一波。
A. My First Sorting Problem
题意 :
给你两个整数 x x x 和 y y y 。
输出两个整数: x x x 和 y y y 的最小值,以及 x x x 和 y y y 的最大值。
思路:
签到
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;int T,a,b;int main(){cin>>T;while(T--){cin>>a>>b;if(a>b)swap(a,b);cout<<a<<" "<<b<<endl;}return 0;
}
B. Different String
题意:
给你一个由小写英文字母组成的字符串 s s s 。
将 s s s 中的字符重新排列,组成一个新的字符串 r r r ,这个字符串不等于 s s s ,或者报告说这是不可能的。
思路:
如果不可以变成另一个字符串,那么这个字符串一定是由同一个字符组成的。要不然我们就可以选择两个不同的字符交换位置,这样得到的字符串就是不一样的。
我们不妨先选择第一个字符,然后向后找与它不同的字符串,然后交换一下即可。查找不同字符可以使用 string 的成员函数 int string::find_first_not_of(str,pos),它的作用是从第 p o s pos pos 位置开始从前到后寻找第一个不在 s t r str str 中出现的字符,并返回它的下标位置,如果找不到则返回 string::npos。
和它作用类似的还有 find_first_of(),find_last_of(),find_last_not_of()。成员函数 find(str,pos) 的作用是找 str,是子串匹配,而不是找字符。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;int T;
string s;int main(){cin>>T;while(T--){cin>>s;int idx=s.find_first_not_of(s[0],1);if(idx==string::npos)puts("NO");else {puts("YES");swap(s[0],s[idx]);cout<<s<<endl;}}return 0;
}
C. Clock and Strings
题意:
如下图所示,有一个时钟,上面按顺时针顺序标有 1 1 1 到 12 12 12 的数字。
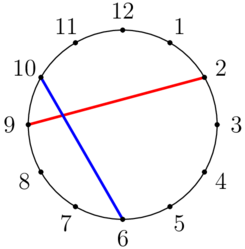
在本例中, ( a , b , c , d ) = ( 2 , 9 , 10 , 6 ) (a,b,c,d)=(2,9,10,6) (a,b,c,d)=(2,9,10,6) 和字符串相交。
爱丽丝和鲍勃有四个不同的整数 a a a 、 b b b 、 c c c 、 d d d ,且不大于 12 12 12 。爱丽丝用红色字符串连接 a a a 和 b b b ,鲍勃用蓝色字符串连接 c c c 和 d d d 。这两条线相交吗?(字符串是直线段)。
思路:
因为题目说了 a , b , c , d a,b,c,d a,b,c,d 互不重复,我们就不考虑相等的特殊情况了。因为 a , b a,b a,b 没有先后顺序,所以不妨令 a < b a<b a<b,方便讨论,同理 c < d c<d c<d
手玩一下发现只有 a < c < b < d a<c<b<d a<c<b<d 或者 c < a < d < b c<a<d<b c<a<d<b 两种情况下会相交。判断一下即可。
code:
#include <iostream>
#include <cstdio>
using namespace std;int T,a,b,c,d;int main(){cin>>T;while(T--){cin>>a>>b>>c>>d;if(a>b)swap(a,b);if(c>d)swap(c,d);puts(((a<c && c<b && b<d) || (c<a && a<d && d<b))?"YES":"NO");}return 0;
}
D. Binary Cut
题意:
给你一个二进制字符串 † ^{\dagger} † 。请找出最少需要切割成多少个片段,以便将得到的片段重新排列成一个有序的二进制字符串。
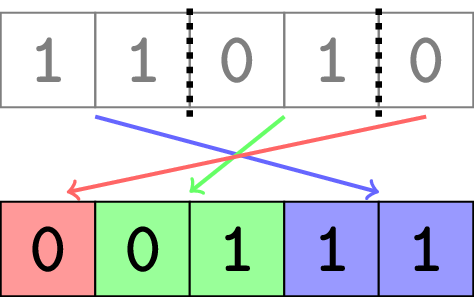
请注意
- 每个字符必须正好位于其中一个片段中;
- 片段必须是原始字符串的连续子串;
- 在重新排列时必须使用所有片段。
† ^{\dagger} † 二进制字符串是由字符 0 \texttt{0} 0 和 1 \texttt{1} 1 组成的字符串。排序后的二进制字符串是指所有字符 0 \texttt{0} 0 都位于所有字符 1 \texttt{1} 1 之前的二进制字符串。
思路:
因为 0 0 0 在前, 1 1 1 在后,因此我们在切割的时候,除了一段可以是前面一段 0 0 0 后面一段 1 1 1 以外,其他的段必须切成全 0 0 0 或全 1 1 1。
考虑前面一段 0 0 0 后面一段 1 1 1 这种怎么切会比较复杂,我们可以把它看成是一个全 0 0 0 段和一个全 1 1 1 段,只不过中间接起来了。这样我们只需要先把原片段切成全 0 0 0 段和全 1 1 1 段就行了,显然我们在 0 → 1 0\rightarrow 1 0→1 和 1 → 0 1\rightarrow 0 1→0 变化的中间切就行了,数一下。
然后我们再把一个全 0 0 0 段和一个全 1 1 1 段中间接起来,当作没切过,在答案上减一。不过我们不能保证原片段一定存在前面一段 0 0 0 后面一段 1 1 1 的情况,所以我们再看一下有没有 0 → 1 0\rightarrow 1 0→1 的变化,没有就说明不能拼起来,也就不能给答案减一。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;int T;
string s;int main(){cin>>T;while(T--){cin>>s;int n=s.length(),cnt=1;bool flag=false;//0->1for(int i=1;i<n;i++){if(s[i-1]=='0' && s[i]=='1')flag=true;if(s[i]!=s[i-1])cnt++;}cout<<cnt-flag<<endl;}return 0;
}
E. Find the Car
题意:
Timur 坐在一辆汽车上,从点 0 0 0 沿数线行驶到点 n n n 。在第 0 0 0 分钟,汽车从第 0 0 0 点开始行驶。
在 0 , a 1 , a 2 , … , a k 0, a_1, a_2, \dots, a_k 0,a1,a2,…,ak 点的直线上有 k + 1 k+1 k+1 个标志,帖木儿知道汽车将分别在 0 , b 1 , b 2 , … , b k 0, b_1, b_2, \dots, b_k 0,b1,b2,…,bk 分钟到达那里。序列 a a a 和 b b b 与 a k = n a_k = n ak=n 严格递增。

在任意两个相邻的标志牌之间,汽车以恒速行驶。帖木儿有 q q q 个查询:每个查询都是一个整数 d d d ,帖木儿希望您输出汽车到达点 d d d 所需的时间,向下取整为最接近的整数。
思路:
有的翻译是错的,向下取整翻译成了四舍五入了,如果有错的可以看一下。
思路还是很明显的,我们在 a a a 数组中二分找到第一个小于等于 d d d 的位置 i i i,我们再从 a i a_i ai 出发匀速走到 d d d,速度可以通过 v = a i + 1 − a i b i + 1 − b i v=\dfrac{a_{i+1}-a_{i}}{b_{i+1}-b_{i}} v=bi+1−biai+1−ai 计算得到。注意特判 d = a k d=a_k d=ak 的情况,因为没有后继节点,是算不出速度的。
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=1e5+5;
typedef long long ll;int T,n,k,q,d;
int a[maxn],b[maxn];int main(){cin>>T;while(T--){cin>>n>>k>>q;for(int i=1;i<=k;i++)cin>>a[i];for(int i=1;i<=k;i++)cin>>b[i];while(q--){cin>>d;if(d==n){cout<<b[k]<<" ";continue;}int i=upper_bound(a,a+k+1,d)-a-1;cout<<b[i]+1ll*(b[i+1]-b[i])*(d-a[i])/(a[i+1]-a[i])<<" ";}cout<<endl;}return 0;
}
F. Circle Perimeter
题意:
给定整数 r r r ,求与 ( 0 , 0 ) (0, 0) (0,0) 的欧氏距离大于或等于 r r r ,但严格小于 r + 1 r+1 r+1 的格点个数。大于或等于 r r r ,但严格小于 r + 1 r+1 r+1 的网格点的个数。
网格点是具有整数坐标的点。从 ( 0 , 0 ) (0, 0) (0,0) 到点 ( x , y ) (x,y) (x,y) 的欧氏距离为 x 2 + y 2 \sqrt{x^2 + y^2} x2+y2。
思路:
我们可以先算出半径为 r + 1 r+1 r+1 的圆内点的个数,然后减去半径为 r r r 的圆内点的个数,答案即为所求。
听同学说是个高斯圆问题,也就是圆内整点问题。这个问题有一些数学家的猜想之类的,不过也仅限于猜想。这个题给定 ∑ r = 1 0 5 \sum r=10^5 ∑r=105,数据范围其实并不大,所以不用数学家的奇淫寄巧,直接暴力也是可做滴。

我们可以先计算图中红色部分的圆内点的个数,然后乘以 4 4 4 就可以得到所有点的个数了。计算红色部分的点的个数,我们可以枚举 1 ∼ r 1\sim r 1∼r 的每一列(因为圆的半径只有 r r r,所以最远到第 r r r 列,外面就没点了),分别计算第 i i i 列有多少个点,累加起来即可。
这样计算出来的是半径为 r r r 的圆的点,我们再算一遍半径为 r + 1 r+1 r+1 的圆的点,后者减去前者即可。或者我们在算每一列的时候,直接算出在半径 r + 1 r+1 r+1 但不在 r r r 内的点的个数。
code:
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const int maxn=1e5+5;
typedef long long ll;ll T,r;ll ge(ll x){\\最小的>=x的数if(x<0)return 0;ll t=sqrt(x);while(t*t<x)t++;return t;
}
ll lt(ll x){\\最大的<x的数ll t=sqrt(x)+1;while(t*t>=x)t--;return t;
}int main(){cin>>T;while(T--){cin>>r;ll ans=0;for(ll i=1;i<=r;i++){ans+=lt((r+1)*(r+1)-i*i)-ge(r*r-i*i)+1;} cout<<ans*4<<endl;}return 0;
}
G. XOUR
题意:
给你一个由 n n n 个非负整数组成的数组 a a a 。
如果 a i X O R a j < 4 a_i~\mathsf{XOR}~a_j < 4 ai XOR aj<4 ,你可以交换位置 i i i 和 j j j 的元素,其中 X O R \mathsf{XOR} XOR 是 按位异或。
求任意交换次数所能组成的词法最小数组。
如果在 x x x 和 y y y 相差的第一个位置上,有 x i < y i x_i < y_i xi<yi ,那么数组 x x x 在词法上比数组 y y y 小。
思路:
如果 a i ⊕ a j < 4 a_i\oplus a_j<4 ai⊕aj<4 说明它们的二进制位在高位上是完全相同的,而最低的两位上则完全不受限制。所以我们不看低两位,如果高位相同的话,它们之间就可以相互交换位置,否则就不能。
我们把若干个高位相同的数提取出来,然后排个序,再放回空位上,对每一堆高位相同的数都做这样的操作,最后得到的就是词法最小数组。
写法应该很多,这里就给一个我自己的写法。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#define pii pair<int,int>
using namespace std;
const int maxn=2e5+5;int T,n,a[maxn];
map<int,priority_queue<int,vector<int>,greater<int> > > val;int main(){cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];val[a[i]>>2].push(a[i]);}for(int i=1;i<=n;i++){auto &b=val[a[i]>>2];cout<<b.top()<<" ";b.pop();}cout<<endl;}return 0;
}
H. ±1
题意:
鲍勃有一个行数为 3 3 3 列数为 n n n 的网格,其中每一行都包含某个整数 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n 的 a i a_i ai 或 − a i -a_i −ai 。例如, n = 4 n=4 n=4 可能包含的网格如下所示:
[ a 1 − a 2 − a 3 − a 2 − a 4 a 4 − a 1 − a 3 a 1 a 2 − a 2 a 4 ] \begin{bmatrix} a_1 & -a_2 & -a_3 & -a_2 \\ -a_4 & a_4 & -a_1 & -a_3 \\ a_1 & a_2 & -a_2 & a_4 \end{bmatrix} a1−a4a1−a2a4a2−a3−a1−a2−a2−a3a4
爱丽丝和鲍勃玩的游戏如下:
- 鲍勃向爱丽丝展示他的网格。
- 爱丽丝给鲍勃一个她自己选择的数组 a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an ,其中的元素都是 − 1 \mathbf{-1} −1 或 1 \mathbf{1} 1。
- 鲍勃将这些值代入他的网格,组成一个由 − 1 -1 −1 和 1 1 1 组成的网格。
- 鲍勃将每一列中的元素按单调不减的顺序排列。
- 如果中间一行的所有元素都是 1 1 1 ,则爱丽丝获胜;否则,鲍勃获胜。
例如,假设爱丽丝给鲍勃提供了上述网格的数组 [ 1 , − 1 , − 1 , 1 ] [1, -1, -1, 1] [1,−1,−1,1] 。那么会发生以下情况(为清晰起见,添加了颜色):
[ a 1 − a 2 − a 3 − a 2 − a 4 a 4 − a 1 − a 3 a 1 a 2 − a 2 a 4 ] → [ 1 , − 1 , − 1 , 1 ] [ 1 1 1 1 − 1 1 − 1 1 1 − 1 1 1 ] → sort each column [ − 1 − 1 − 1 1 1 1 1 1 1 1 1 1 ] \begin{bmatrix} \color{red}{a_1} & \color{green}{-a_2} & \color{blue}{-a_3} & \color{green}{-a_2} \\ -a_4 & a_4 & \color{red}{-a_1} & \color{blue}{-a_3} \\ \color{red}{a_1} & \color{green}{a_2} & \color{green}{-a_2} & a_4 \end{bmatrix} \xrightarrow{[\color{red}{1},\color{green}{-1},\color{blue}{-1},1]} \begin{bmatrix} \color{red}{1} & \color{green}{1} & \color{blue}{1} & \color{green}{1} \\ -1 & 1 & \color{red}{-1} & \color{blue}{1} \\ \color{red}{1} & \color{green}{-1} & \color{green}{1} & 1 \end{bmatrix} \xrightarrow{\text{sort each column}} \begin{bmatrix} -1 & -1 & -1 & 1 \\ \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} \\ 1 & 1 & 1 & 1 \\ \end{bmatrix}\, a1−a4a1−a2a4a2−a3−a1−a2−a2−a3a4 [1,−1,−1,1] 1−1111−11−11111 sort each column −111−111−111111
由于中间一行都是 1 1 1 ,因此爱丽丝获胜。
给定鲍勃的网格,判断爱丽丝是否可以选择数组 a a a 来赢得游戏。
思路:
年轻人的第一个 2 − s a t 2-sat 2−sat,不会的就百度吧,这题很板。
有代码
详细讲解(有输出选取方案)
OI-wiki 主要是看这个 ⇒ 主要是看这个\Rightarrow 主要是看这个⇒2-sat 各种性质的证明
上面的文档里比较重要的性质有:
- 2 − s a t 2-sat 2−sat 构造出的原图中,关系具有对称性和传递性。
- 构造出的原图可能有强连通分量,连通分量中的点必须同时选取或者同时不选,对所有极大连通子图进行缩点,得到的新图就是一个有向无环图(DAG)。新图与原图等价,也具有对称性和传递性。
- 假设新图中的某个点为 S i S_i Si,对应矛盾点为 S i ′ S'_i Si′。对任意一对 S i , S i ′ S_i,S'_i Si,Si′, S i S_i Si 的后继节点与 S i ′ S'_i Si′ 的前代节点相互对称。
- 若问题无解,则在原图上必然存在一对 A i , A i ′ A_i,A'_i Ai,Ai′,使得 A i , A i ′ A_i,A'_i Ai,Ai′ 同属一个环(也就是在一个强连通分量中)。反之,如果每一对 A i , A i ′ A_i,A'_i Ai,Ai′ 都不属于同一个环,则问题一定有解。我们可以通过拓扑序从底向上 O ( n ) O(n) O(n) 选出一组可行解。
因为要求中间一行都是 1 1 1,所以 − 1 -1 −1 的个数不能大于 1 1 1,所以如果一列三个元素的其中一个是 − 1 -1 −1 的话,那么其他两个元素都必须是 1 1 1。
假设这三个元素分别是 x , y , z x,y,z x,y,z 的话。如果 x x x 取 − 1 -1 −1,那么就可以推出 y , z y,z y,z 取 1 1 1。用 2 − s a t 2-sat 2−sat 来做的话,其实也就是连边 − x → y , − x → z -x\rightarrow y,-x\rightarrow z −x→y,−x→z,同理,还有连 − y → x , − y → z , − z → x , − z → y -y\rightarrow x,-y\rightarrow z,-z\rightarrow x,-z\rightarrow y −y→x,−y→z,−z→x,−z→y。
连好边之后就是很板的 2 − s a t 2-sat 2−sat。我们直接检查一下每个点和它的矛盾点不在同一个强连通块内即可(也就是上面的性质 4 4 4)。
code:
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int maxn=505;int T,n;
int a[maxn][3];
int id(int x){return (x<0)?-x+n:x;}vector<int> g[maxn<<1];int dfn[maxn<<1],low[maxn<<1],idx;
bool ink[maxn<<1];
int belong[maxn<<1],cnt;
//vector<vector<int> > scc;
vector<int> stk;
void tarjan(int u){dfn[u]=low[u]=++idx;stk.push_back(u);ink[u]=true;for(auto v:g[u]){if(!dfn[v]){tarjan(v);low[u]=min(low[v],low[u]);}else if(ink[v])low[u]=min(low[u],dfn[v]);}if(low[u]==dfn[u]){int nd;++cnt;do{nd=stk.back();stk.pop_back();ink[nd]=false;belong[nd]=cnt;}while(nd!=u);}
}int main(){cin>>T;while(T--){cin>>n;for(int j=0;j<3;j++)for(int i=1;i<=n;i++)cin>>a[i][j];idx=cnt=0;for(int i=1;i<=2*n;i++){g[i].clear();dfn[i]=low[i]=belong[i]=0;}for(int i=1,x,y,z;i<=n;i++){x=a[i][0];y=a[i][1];z=a[i][2];
// cout<<x<<" "<<y<<" "<<z<<endl;g[id(-x)].push_back(id(y));g[id(-x)].push_back(id(z));g[id(-y)].push_back(id(x));g[id(-y)].push_back(id(z));g[id(-z)].push_back(id(x));g[id(-z)].push_back(id(y));}for(int u=1;u<=2*n;u++)if(!dfn[u])tarjan(u);bool flag=true;for(int u=1;u<=n;u++){if(belong[id(u)]==belong[id(-u)])flag=false;}puts((flag)?"YES":"NO");}return 0;
}