本文前段文链接：
https://blog.csdn.net/gongdiwudu/article/details/138854033?spm=1001.2014.3001.5501

一、说明

   关于流体物质的仿真和模拟，需要流体理论方面的一般知识。我们这里从基本流体方程入手，详细解释如何实现流体仿真的每一个具体步骤。

二、我们的算法

2.1 设置

   我们的实现既处理流体的运动，也处理任意数量物质的流体传播，例如质量密度、温度或纹理坐标。每个量都在二维(NDIM=2) 或三维 (NDIM=3) 上定义网格，取决于应用。网格由其物理尺寸定义：每个网格的原点 O[NDIM] 和长度 L[NDIM]边，以及每个坐标中的单元格数量 N[NDIM]。这进而确定每个体素的大小D[i]=L[i]/N[i]。这网格的定义是我们程序的输入，由动画师指定。速度场定义在每个细胞如图 3 所示。请注意，以前的研究人员，例如，[7]定义了细胞边界的速度。我们更喜欢以单元格为中心的网格，因为它更容易实现。我们为速度的每个分量分配两个网格：U0[NDIM] 和 U1[NDIM]。在我们模拟的每个时间步一个网格对应于上一步获得的解。
   我们将新的解决方案存储在第二个网格中。每一步之后，网格被交换。我们还分配两个网格来保存标量场对应于流动所输送的物质。虽然我们的实施可以处理任意数量的物质，因为为清楚起见，我们在本节中仅介绍一个字段的算法。
   该标量存储在网格 S0 和 S1 中。速度为交互性由单个时间步长 dt 控制，可以表示为正如动画师所希望的那样大，因为我们的算法是流体的物理特性是其粘度的函数单独粘。通过改变粘度，动画师可以模拟范围广泛的物质，从​​胶状物质到高度湍流。物质的属性通过以下方式建模扩散常数kS和耗散率aS。连同这些参数，动画师还必须指定这些字段的值在网格的边界上。基本上有两种类型：定期或固定。边界条件可以是不同类型对于每个坐标。当选择周期性边界条件时，流体会环绕。这意味着一块液体离开一侧的网格，重新进入另一侧的网格。
   在边界固定的情况下，各物理量的值必须在网格的边界处指定。最简单的方法就是在边界处将场设置为零。我们建议读者参考福斯特和梅塔克萨斯的论文对不同的问题进行了精彩的描述边界条件及其产生的影响[7]。在结果中在本节中，我们描述了为每个图像选择的边界条件。对于边界条件为的特殊情况每个坐标都是周期性的，一个基于快速的非常优雅的求解器可以采用傅立叶变换。该算法描述于
   第 2.3 节。由于本节中的求解器，我们在此不再重复更通用，可以处理两种类型的边界条件。
通过向流体施加外力使其运动。
   我们编写了一个动画系统，其中动画师具有鼠标可以向流体施加定向力。势力可以也可以是流体中其他物质的函数。例如，穿过流体的温度场可以产生浮力和汹涌的力量。在我们的系统中，我们允许用户创建各个字段之间的各种依赖关系，其中一些在本文的结果部分中进行了描述。我们不描述我们的动画系统非常详细，因为它的功能应该从下一节的例子中可以明显看出。相反，我们专注于在我们的模拟器上，它采用由动画师作为输入。

2.2 模拟器

   一旦我们弄清楚了纳维-斯托克斯方程的数学原理有了第 2 节中的方程，我们的实现就变得简单了。我们想强调的是，理论的发展第 2 节绝不是无缘无故的，但对于编写紧凑型求解器非常有用。特别是，将问题转化为数学环境使我们能够利用庞大的体量偏微分方程数值分析中所做的工作。我们已将求解器编写为单独的例程库由交互式动画系统调用。整个库仅包含大约 500 行 C 代码。两个主要该库的例程更新速度场 Vstep 或给定时间步长内的标量场 Sstep。我们假设外力由向量数组 F[NDIM] 给出，并且源由标量场的数组 Ssource 给出。这我们模拟器的总体结构如下所示

while ( simulating ) f
/* handle display and user interaction */
/* get forces F and sources Ssource from the UI */
Swap(U1,U0); Swap(S1,S0);
Vstep ( U1, U0, visc, F, dt );
Sstep ( S1, S0, kS, aS, U1, Ssource, dt );

速度求解器由四个步骤组成： 添加力到场，场自身平流，场由于以下原因而扩散流体内的粘性摩擦，最后一步的速度为被迫保存质量。该例程的总体结构为：

Vstep ( U1, U0, visc, F, dt )
for(i=0;i<NDIM;i++)
addForce ( U0[i], F[i], dt );
for(i=0;i<NDIM;i++)
Transport ( U1[i], U0[i], U0, dt );
for(i=0;i<NDIM;i++)
Diffuse ( U0[i], U1[i], visc, dt );
Project ( U1, U0, dt );

   标量场求解器的一般结构与多于。包括四个步骤：添加源、传输字段速度、扩散并最终消散场。标量场求解器共享速度求解器调用的一些例程：

Sstep ( S1, S0, k, a, U, source, dt )
addForce ( S0, source, dt );
Transport ( S1, S0, U, dt );
Diffuse ( S0, S1, k, dt );
Dissipate ( S1, S0, a, dt );

   addForce 例程将力场乘以时间相加步骤到字段的每个值。消散例程 Dissipate将第一个数组的每个元素除以 1+dt*a 并存储在新数组中。运输例程是我们的关键一步模拟。它解释了物质的运动速度场。更重要的是，它用于解决纳维-斯托克斯方程的非线性问题。总体结构为这个例程（在三维空间中）是

Transport ( S1, S0, U, dt )
for each cell (i,j,k) do
X = O+(i+0.5,j+0.5,k+0.5)*D;
TraceParticle ( X, U, -dt, X0 );
S1[i,j,k] = LinInterp ( X0, S0 );
end

   例程 TraceParticle 跟踪从 X 开始到时间 -dt 内的场 U。这条路径的终点是新的点 X0。我们使用简单的二阶龙格库塔 (RK2)粒子追踪方法 [14] 和自适应粒子追踪器，仅在高速梯度区域（例如靠近物体边界）对时间步进行二次采样。 LinInterp 例程在该位置线性插值标量场 S 的值X0。我们注意到我们没有使用更高阶的插值，因为这可能会由于振荡和超调而导致不稳定此类插值所固有的。另一方面，高阶样条可以使用近似值，尽管这些趋于平滑所产生的流。
   为了求解扩散 (Diffuse) 并执行投影 (Project)，我们需要一个稀疏线性求解器 SolveLin。这最好的理论选择是多重网格算法[10]。然而，我们使用了 FISPAK 库中的求解器，因为它很容易合并到我们的代码中并给出了良好的结果 [22]1。在实践中，事实证明，它比我们实施多重网格要快算法。在附录 B 中，我们准确地展示了这些例程是如何进行的用于执行漫反射步骤和项目步骤。这些例程非常适合没有内部边界的域。当复杂的边界或对象位于流内时，可以要么使用复杂的多网格求解器，要么使用良好的松弛例程 [9]。无论如何，我们的模拟器可以轻松适应新的求解器。

三、计算结果

   我们的纳维-斯托克斯求解器可用于许多需要类流体运动的应用。我们已经实施了两个和交互式建模器中的三维求解器允许用户与流体实时交互。运动已建模通过增加流体密度或施加力。这然后使用我们的计算速度和密度的演变求解器。为了进一步增加流程的视觉复杂性，我们为密度添加纹理细节。通过移动纹理坐标还使用标量求解器，我们实现了高度详细的流程。到补偿纹理贴图所经历的高度扭曲，我们使用三组纹理坐标，它们会定期重置到它们的初始（未受干扰的）值。每时每刻所产生的纹理贴图是这三个纹理贴图的叠加。这这个想法最初是由 Max 等人提出的。 [13]。图 4.(a) 显示了动画中的一系列帧用户与我们的一种液体纹理进行交互。图SIGGRAPH 会议记录的封底是另一个框架
具有较大网格尺寸的相似序列（1002）。

   图 4.(b) 到 4.(g) 显示了各种动画的帧我们使用三维解算器生成的。在每种情况下这些动画是通过允许动画师实时放置密度和施加力来创建的。气体按体积绘制使用三维硬件纹理映射功能我们的 SGI Octane 工作站。我们还添加了一个单通道计算来自定向光源的自阴影效果一个固定的位置。显然，用更复杂的渲染可以进一步提高渲染质量硬件或软件。我们的网格大小范围为 163至 303和帧速率足够快以监控动画，同时能够来控制他们的行为。在大多数动画中，我们添加了“噪声”项与密度量成正比（比例因子是用户定义的参数）。这在我们的一些动画中产生了漂亮的滚滚运动。在图 4.(d)-(e) 中们使用了分形纹理贴图，而在图 4.(g) 中我们使用了分形纹理贴图。我们使用了由均匀间隔的线条组成的纹理贴图。我们所有的动画都是在配备 R10K 处理器和 192 MB 内存的 SGI Octane 工作站上创建的。

四、结论

   本文的动机是创建一个通用软件系统，允许动画师实时设计类似流体的运动。我们最初的目的是将我们的系统建立在 Foster 和 Metaxas 的基础上工作。然而，他们的方法固有的不稳定性迫使我们开发新的算法。我们的求解器具有如下属性无条件稳定，可以处理多种流体二维和三维。随之而来的结果
   论文清楚地表明我们的解算器足够强大，可以让动画师实现许多类似流体的效果。我们因此相信我们的求解器比以前的求解器有了实质性的改进在这个领域工作。然而，这里展示的工作并没有贬低以前的、更以视觉为导向的模型。特别是，我们相信我们的流体解算器与固体纹理的结合，例如，可能是未来研究的一个有前途的领域[4]。我们的流体求解器可用于生成整体运动，而坚实的纹理可以添加额外的细节以获得更高质量的动画。
   此外，我们还没有解决模拟流体的问题自由边界，例如水[6]。这个问题相当大更困难的是，因为边界的几何形状随着时间的推移而动态变化。然而，我们希望我们的稳定求解器可以也适用于这个问题。此外，我们希望延长我们的有限元边界拟合网格的求解器。我们正在调查此类扩展。

五、特征方法

   特征法可用于求解以下类型的平流方程

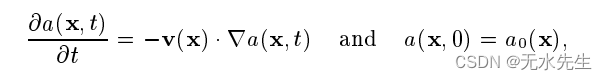
   其中 a 是标量场，v 是稳定向量场，a0 是场在时间 t = 0 时。令 p(x0; t) 表示向量的特征场 v 在 t = 0 时流经点 x0：

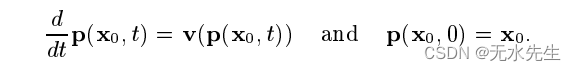
   现在让 a (x0; t) = a(p(x0; t); t) 为沿t = 0 时通过点 x0 的特性。变化这个数量随时间的变化可以使用链式法则计算区分：

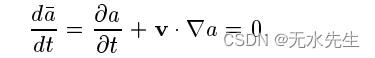
   这表明标量的值不随精简。特别是，我们有 (x0; t)= a(x0; 0) = a0(x0)。因此，初始场和特征完全定义了解决平流问题。给定时间 t 的场和位置 x 是通过首先追溯位置 x 的时间来计算的沿着特征得到点x0，然后评估此时的初始字段：

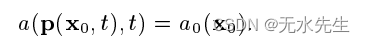
   我们用这种方法来求解一段时间内的平流方程间隔 [t; t + t] 为流体。在这种情况下，v = u(x; t) 且 a0 为时间 t 时流体速度的任何分量。

六、FISHPAK 例程

   FISHPAK 的线性求解器 POIS3D 旨在求解有限差分方程的一般系统：

K1*(S[i-1,j,k]-2*S[i,j,k]+S[i+1,j,k]) +
K2*(S[i,j-1,k]-2*S[i,j,k]+S[i,j+1,k]) +
A[k]*S[i,j,k-1]+B[k]*S[i,j,k]+

   对于扩散求解器，左侧常数的值侧面是：

K1 = -dt*k/(D[0]*D[0]),
K2 = -dt*k/(D[1]*D[1]),
A[k] = C[k] = -dt*k/(D[2]*D[2]) and
B[k] = 1+2*dt*k/(D[2]*D[2]),

   而右侧等于包含前一个的网格解：F=S0。在投影步骤中，这些常数等于

K1 = 1/(D[0]*D[0]), K2 = 1/(D[1]*D[1]),
A[k] = C[k] = 1/(D[2]*D[2]) and
B[k] = -2/(D[2]*D[2]),

   而右侧等于速度的散度场地：

F[i,j,k] = 0.5*((U[i+1,j,k]-U[i-1,j,k])/D[0]+
(U[i,j+1,k]-U[i,j-1,k])/D[1]+
(U[i,j,k+1]-U[i,j,k-1])/D[2]).

   然后从之前的解中减去解的梯度解决方案：

U1[0][i,j,k] = U0[0][i,j,k] -
0.5*(S[i+1,j,k]-S[i-1,j,k])/D[0],
U1[1][i,j,k] = U0[1][i,j,k] -
0.5*(S[i,j+1,k]-S[i,j-1,k])/D[1],
U1[2][i,j,k] = U0[2][i,j,k] -
0.5*(S[i,j,k+1]-S[i,j,k-1])/D[2].

   FISHPAK 例程还能够处理不同类型的边界条件，周期性的和固定的。

七、参考资料

  
References
[1] M. B. Abbott. Computational Fluid Dynamics: An Introduction for Engineers. Wiley, New York, 1989.
[2] J. X. Chen, N. da Vittoria Lobo, C. E. Hughes, and J. M.Moshell. Real-Time Fluid Simulation in a Dynamic Virtual Environment. IEEE Computer Graphics and Applications,
pages 52–61, May-June 1997.
[3] A. J. Chorin and J. E. Marsden. A Mathematical Introduction to Fluid Mechanics. Springer-Verlag. Texts in Applied Mathematics 4. Second Edition., New York, 1990.
[4] D. Ebert, K. Musgrave, D. Peachy, K. Perlin, and S. Worley.
Texturing and Modeling: A Procedural Approach. AP Professional, 1994.
[5] D. S. Ebert, W. E. Carlson, and R. E. Parent. Solid Spaces and Inverse Particle Systems for Controlling the Animation of Gases and Fluids. The Visual Computer, 10:471–483, 1994.
[6] N. Foster and D. Metaxas. Realistic Animation of Liquids. Graphical Models and Image Processing, 58(5):471–483, 1996.
[7] N. Foster and D. Metaxas. Modeling the Motion of a Hot,Turbulent Gas. In Computer Graphics Proceedings, Annual Conference Series, 1997, pages 181–188, August 1997.
[8] M. N. Gamito, P. F. Lopes, and M. R. Gomes. Twodimensional Simulation of Gaseous Phenomena Using Vortex Particles. In Proceedings of the 6th Eurographics Workshop on Computer Animation and Simulation, pages 3–15.Springer-Verlag, 1995.
[9] M. Griebel, T. Dornseifer, and T. Neunhoeffer. Numerical Simulation in Fluid Dynamics: A Practical Introduction.SIAM, Philadelphia, 1998.
[10] W. Hackbusch. Multi-grid Methods and Applications.Springer Verlag, Berlin, 1985.
[11] F. H. Harlow and J. E. Welch. Numerical Calculation of
Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface. The Physics of Fluids, 8:2182–2189, December 1965.
[12] M. Kass and G. Miller. Rapid, Stable Fluid Dynamics for Computer Graphics. ACM Computer Graphics (SIGGRAPH’90), 24(4):49–57, August 1990.
[13] N. Max, R. Crawfis, and D. Williams. Visualizing Wind Velocities by Advecting Cloud Textures. In Proceedings of Visualization ’92, pages 179–183, Los Alamitos CA, October
1992. IEEE CS Press.
[14] W. H. Press, B. P. Flannery, S. A. Teukolsky, and W. T. Vetterling. Numerical Recipes in C. The Art of Scientific Computing.Cambridge University Press, Cambridge, 1988.
[15] W. T. Reeves. Particle Systems. A Technique for Modeling a Class of Fuzzy Objects. ACM Computer Graphics (SIGGRAPH ’83), 17(3):359–376, July 1983.
[16] M. Shinya and A. Fournier. Stochastic Motion - Motion Under the Influence of Wind. In Proceedings of Eurographics ‘92,pages 119–128, September 1992.
[17] K. Sims. Particle Animation and Rendering Using Data Parallel Computation. ACM Computer Graphics (SIGGRAPH ’90),24(4):405–413, August 1990.
[18] K. Sims. Choreographed Image Flow. The Journal Of Visualization And Computer Animation, 3:31–43, 1992.
[19] J. Stam. A General Animation Framework for Gaseous Phenomena. ERCIM Research Report, R047, January 1997.
http://www.ercim.org/publications/technical reports/047-abstract.html.
[20] J. Stam and E. Fiume. Turbulent Wind Fields for Gaseous Phenomena. In Proceedings of SIGGRAPH ’93, pages 369–376. Addison-Wesley Publishing Company, August 1993.
[21] J. Stam and E. Fiume. Depicting Fire and Other Gaseous Phenomena Using Diffusion Processes. In Proceedings of SIGGRAPH ’95, pages 129–136. Addison-Wesley Publishing
Company, August 1995.
[22] P. N. Swarztrauber and R. A. Sweet. Efficient Fortran Subprograms for the Solution of Separable Elliptic Partial Differential Equations. ACM Transactions on Mathematical Software,
5(3):352–364, September 1979.
[23] J. Wejchert and D. Haumann. Animation Aerodynamics. ACM Computer Graphics (SIGGRAPH ’91), 25(4):19–22, July 1991.
[24] L. Yaeger and C. Upson. Combining Physical and Visual Simulation. Creation of the Planet Jupiter for the Film 2010. ACM Computer Graphics (SIGGRAPH ’86), 20(4):85–93, August
1986.