最小二乘分为线性最小二乘和非线性最小二乘
最小二乘目标函数都是min ||f(x)||2
- 若f(x) = ax + b,就是线性最小二乘;
- 若f(x) = ax2 + b / ax2 + bx 之类的,就是非线性最小二乘;
1. 求解线性最小二乘
【参考】

2. 求解非线性最小二乘
需要用到牛顿法,高斯牛顿法,或者LM法
目标函数都是min F(x) = min ||f(x)||2
求解的时候需要求解的是f(x)的最小值,其实求解的就是f(x)'=0的地方
(1) 牛顿法/高斯梯度下降
牛顿法是将f(x)进行二阶泰勒展开: f(x)=f(xk)+f’(xk)(x-xk)+1/2 f’‘(xk)(x-xk)2
因为求解的其实是上式的最小值,也就是求解上式导数为0的值
核心迭代等式:xk+1 = xk - f’(xk)/f’'(xk)
其中,一阶导f’(xk)可以看成雅可比矩阵J,二阶导f’'(xk)可以看成海森矩阵H
算法
- 给定初值x0
- 对于第k次迭代,求出一阶导f’(xk)和二阶导f’'(xk)
- 如果f’(xk)足够小则停止;否则xk+1=xk - f’(xk)/f’'(xk),返回2
(2) 高斯牛顿法
这里的f(x)代表的是目标函数F(x)
是将f(x)进行一阶泰勒展开:f(x+dx) = f(x) + J*dx
取得最小值的条件也就是 f(x) + J * dx这个式子对dx的导数为0,
可以求解得到: JTJ * dx = - J * f(x) ,可以简化为 H dx = g,
刚好利用JTJ代替H,减少H计算量
算法
求解等式为 JTJ * dx = - J * f(x),即增量方程,这里的dx也就是每次需要寻找的变化量
- 给定初值x0
- 对于第k次迭代,求出雅可比J(xk) 和f(xk)
- 将以上两值代入,利用方程H dx = g,求解dx
- 如果dx足够小则停止,否则xk+1=xk+dx,返回2
(3) LM法
高斯牛顿本质求解的是xk+1 = xk - H-1 * J(xk) * f(xk) 但是H如果非正定,那 H-1不存在,因此将其加上单位矩阵结局正定问题 :(H + kI)dx = g
计算信赖区间 ρ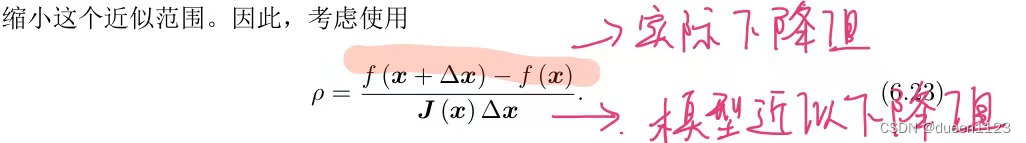
算法
求解等式为 (JTJ+ μI) dx = -J f(x),其中J = J(xk),f(x) = f(xk)
- 给定初值x0
- 对于第k次迭代,求出雅可比J(xk) 和f(xk)
- 计算ρ,若 ρ > 3/4,则 μ = 2μ;
若 ρ < 1/4,则 μ = 0.5μ;- 将J(xk) ,f(xk)和 μ代入,利用方程 (H + μI) dx = g,求解dx
- 如果dx足够小则停止,否则xk+1=xk+dx,返回2
参考
https://zhuanlan.zhihu.com/p/556170185?utm_id=0
https://blog.csdn.net/weixin_43763292/article/details/128060801
https://blog.csdn.net/weixin_41869763/article/details/103603089