场景文本检测识别学习 day09（SSM、S4、Mamba、S6）-编程知识

SSM（State Space Model）

在这里插入图片描述

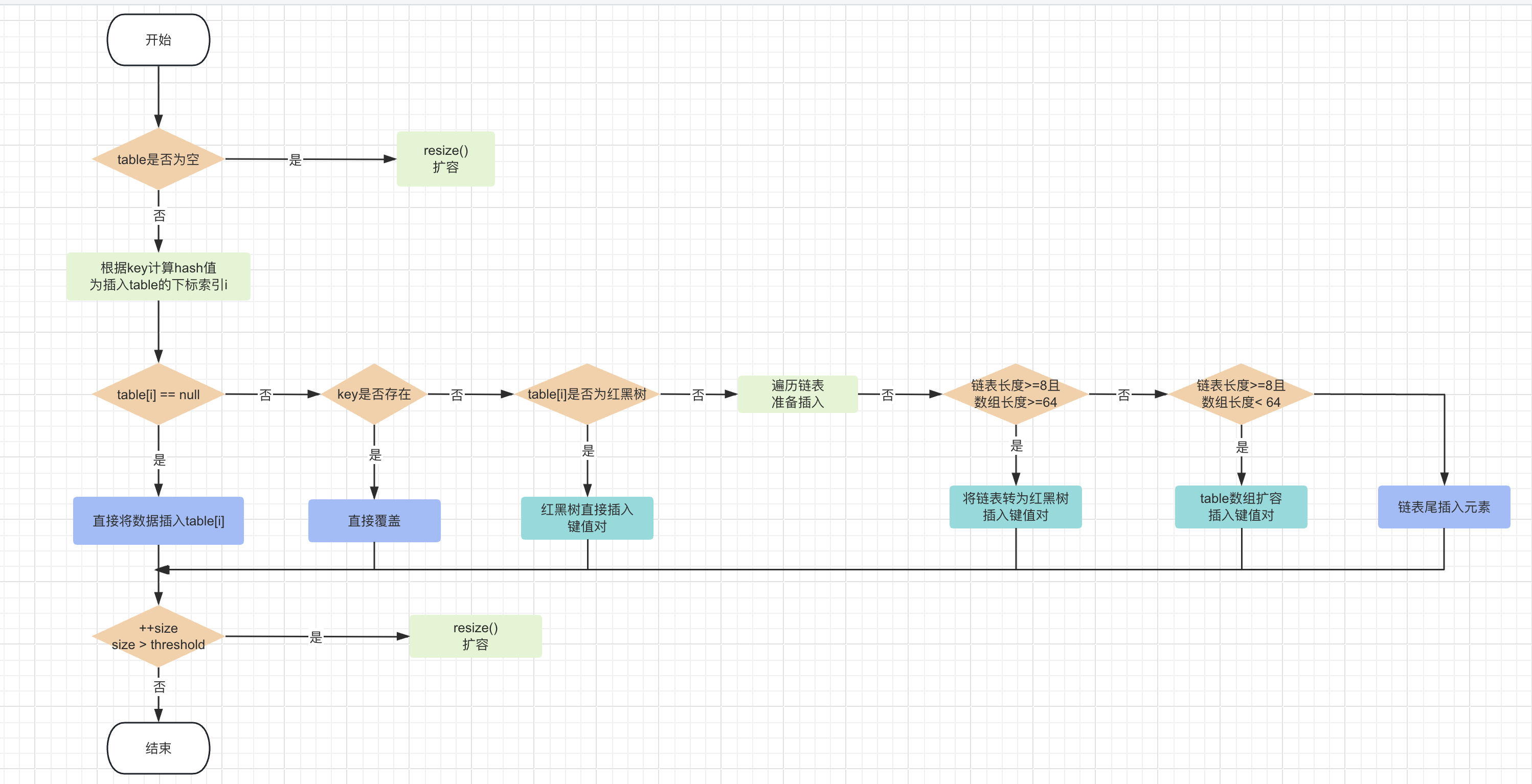
SSM是一个针对连续函数的模型，即输入是连续函数，输出也是连续函数。
上图为状态方程和输出方程，其中h(t)是当前时刻的状态，x(t)是当前时刻的输入，h’(t)是下一个时刻的状态，y(t)是当前时刻的输出。于是上图可以写成下图的形式：
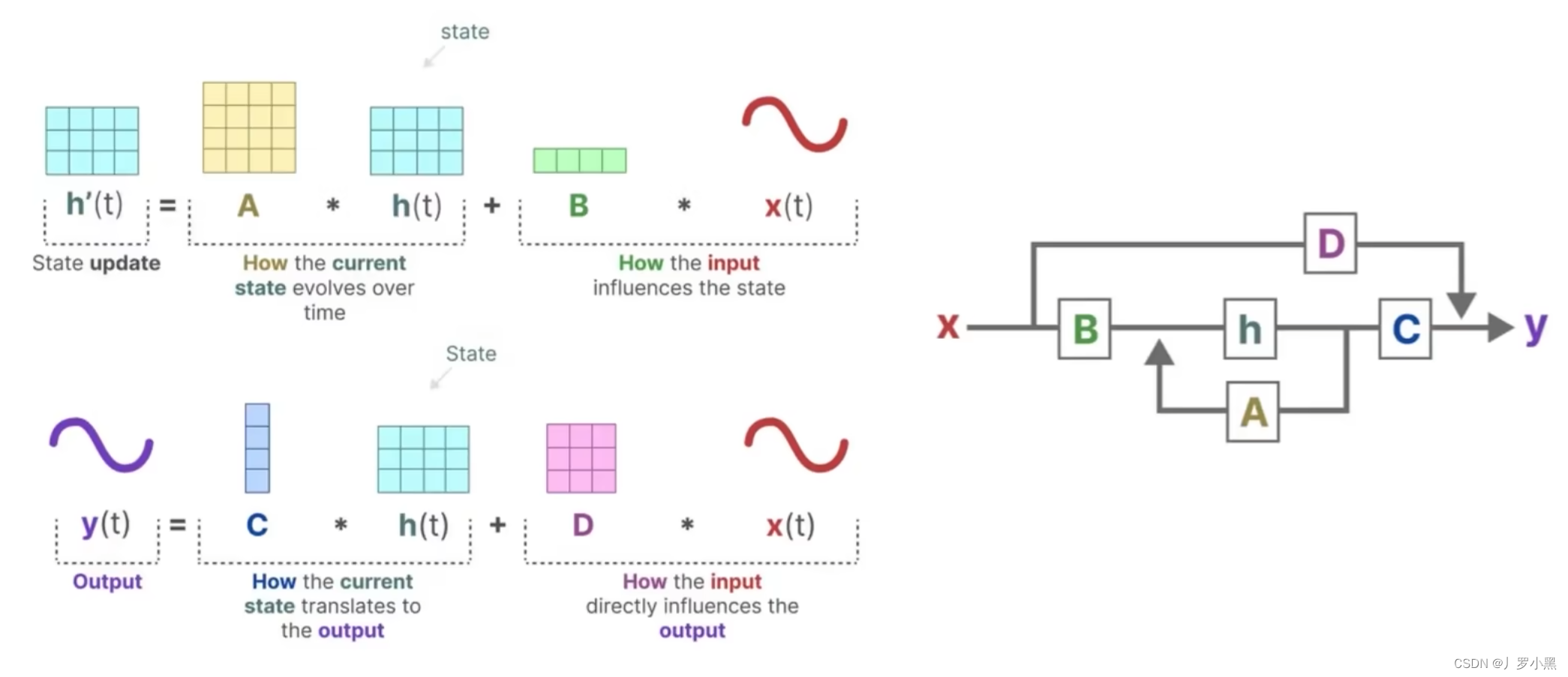
下面是详细的流程图，由于D * x(t)为跳跃连接（res连接），所以在论文中一般都省略，灰色部分为通常意义上的SSM模型流程部分
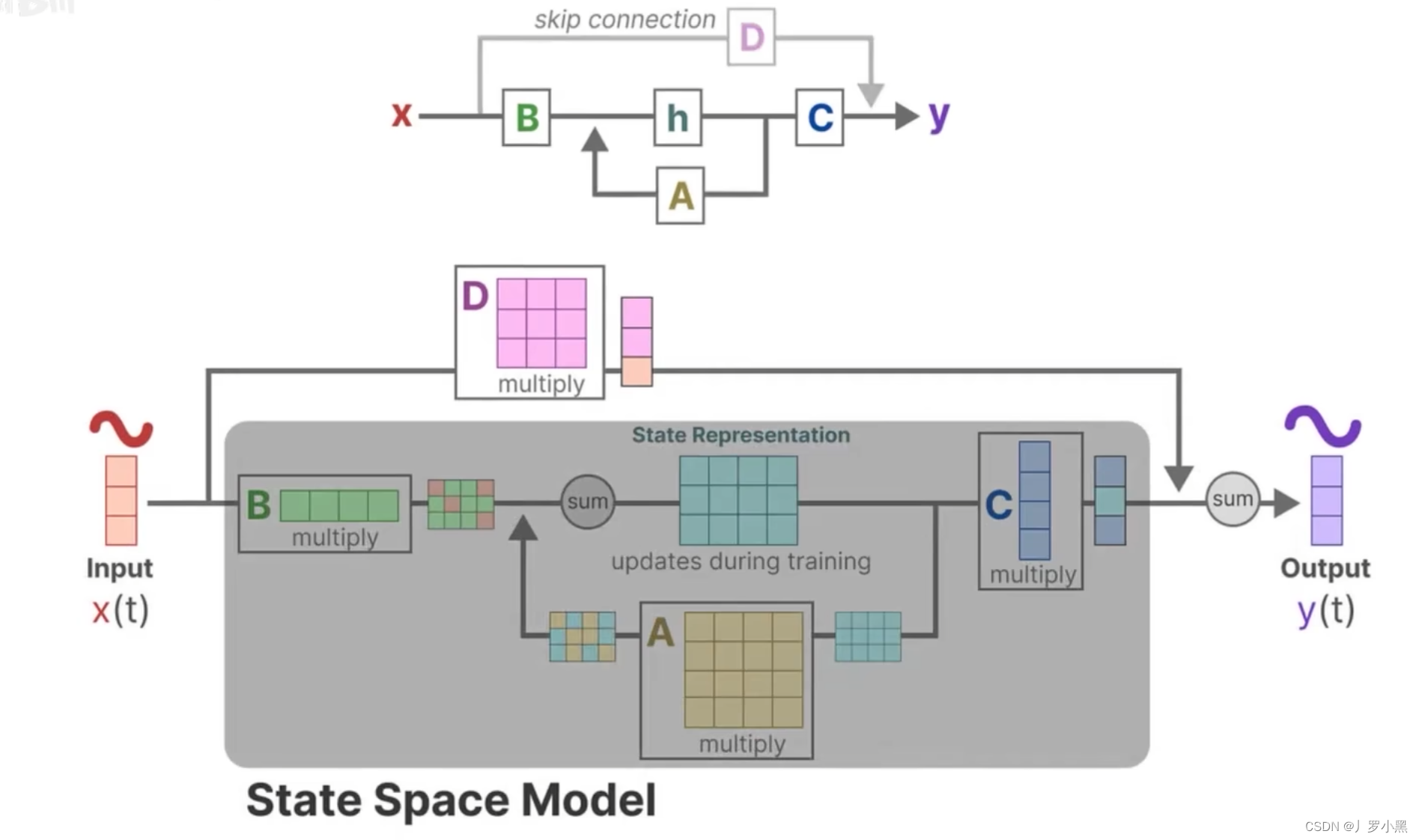
综上，SSM的方程可以写成以下的形式：
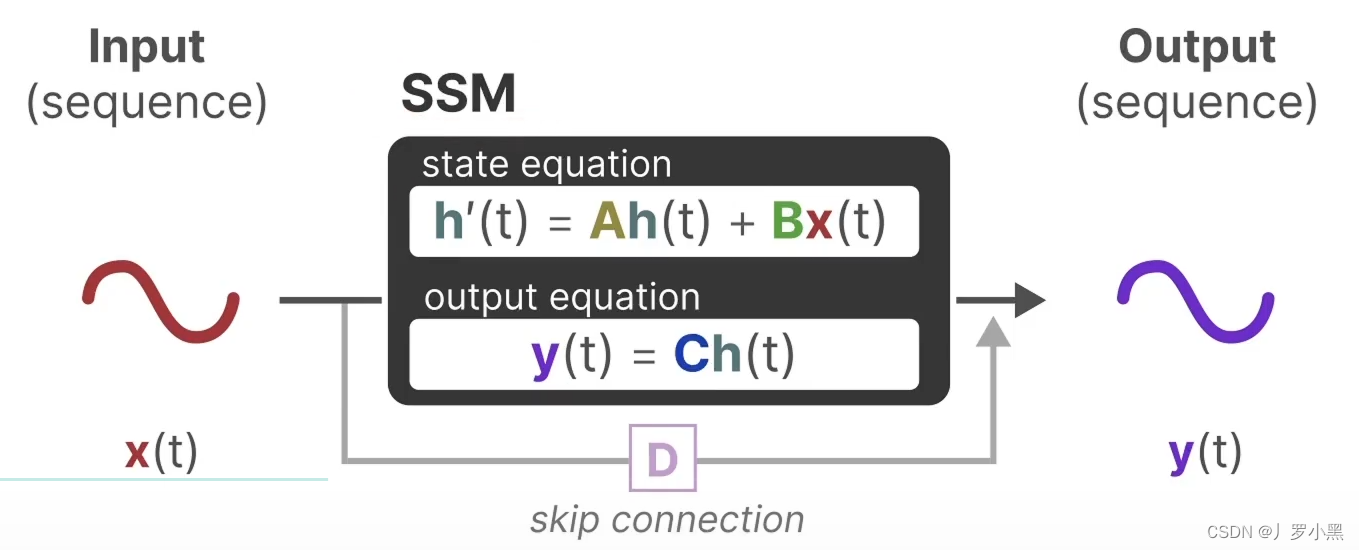
由此可以得出SSM跟RNN很类似，一个拥有状态，一个拥有隐藏状态，如下：

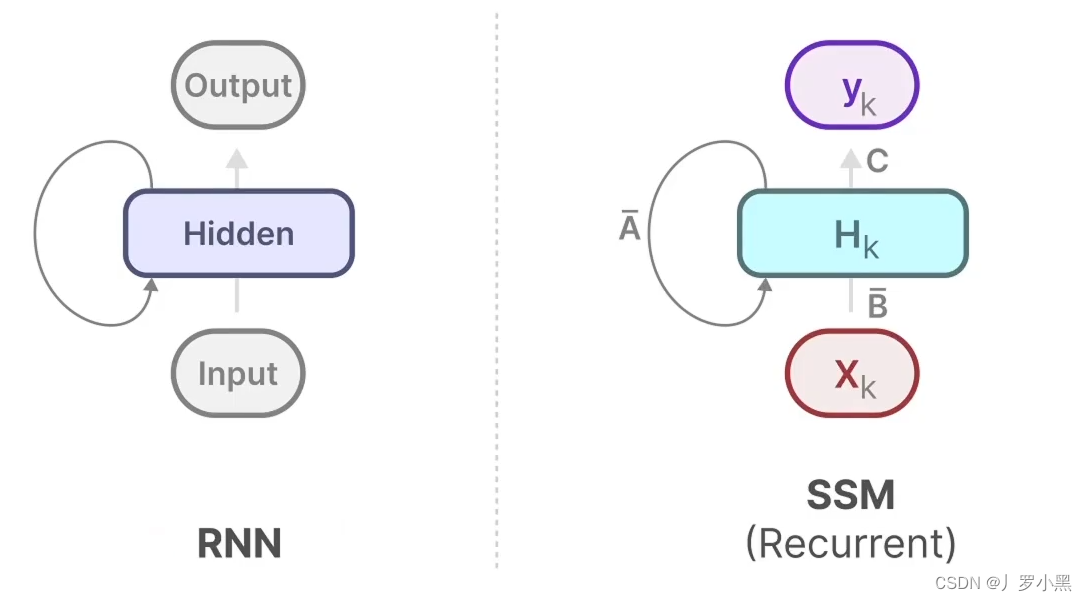
S4模型（Structured State Space Model for Sequence Modeling）

S4模型对SSM的改进有以下三点：
1. 采用零阶保持，来进行连续化：由于SSM模型是针对连续函数的，但是在文本、图像等领域，数据都是离散的，所以我们需要将离散的点连续化，才能输入进SSM模型，最后再从连续的输出中采样离散的点来得到真正的输出
2. 使用卷积结构表示，从而能够并行训练，加快训练速度
3. 使用HIPPO矩阵，解决长距离依赖
先看零阶保持，如下：
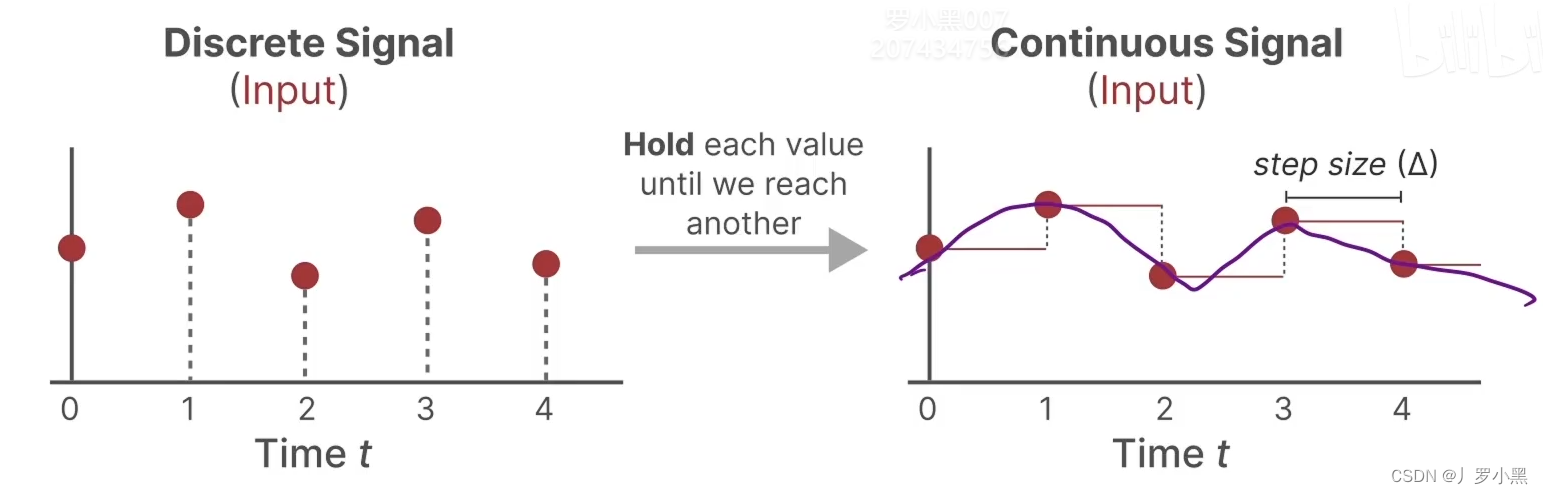
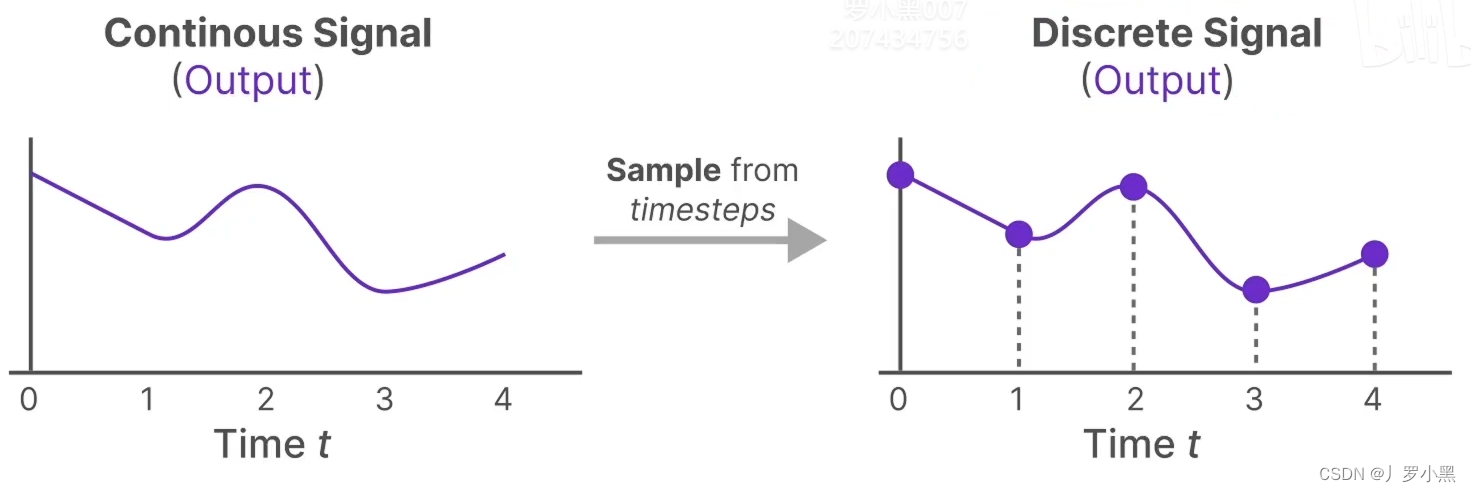
对于离散输入，在每个时间步 $\Delta$ 中，都保持到一个位置上，从而可以使输入连续
对于连续输出，每隔一个时间步 $\Delta$ ，都进行一个采样，从而可以得到离散输出
由于只有A、B矩阵是反应之前状态、输入是如何影响当前状态的（在连续模型中），而C矩阵是反应状态和输出的映射关系（在连续模型和离散模型中是相同的），所以离散化的重点就是离散化那些描述状态是如何随时间改变的连续模型的矩阵，即A、B矩阵。A、B矩阵是常数。
注意：矩阵可以乘函数，但是这个函数得是向量值函数，通常是用来表示系统状态。
相对应的离散化A、B矩阵如下：
那么状态方程和输出方程就变成如下的形式，为了简化，现在的 $h_k$ 表示当前的状态， $h_(k-1)$ 表示之前的状态， $y_k$ 表示当前的输出， $x_k$ 表示当前的输入
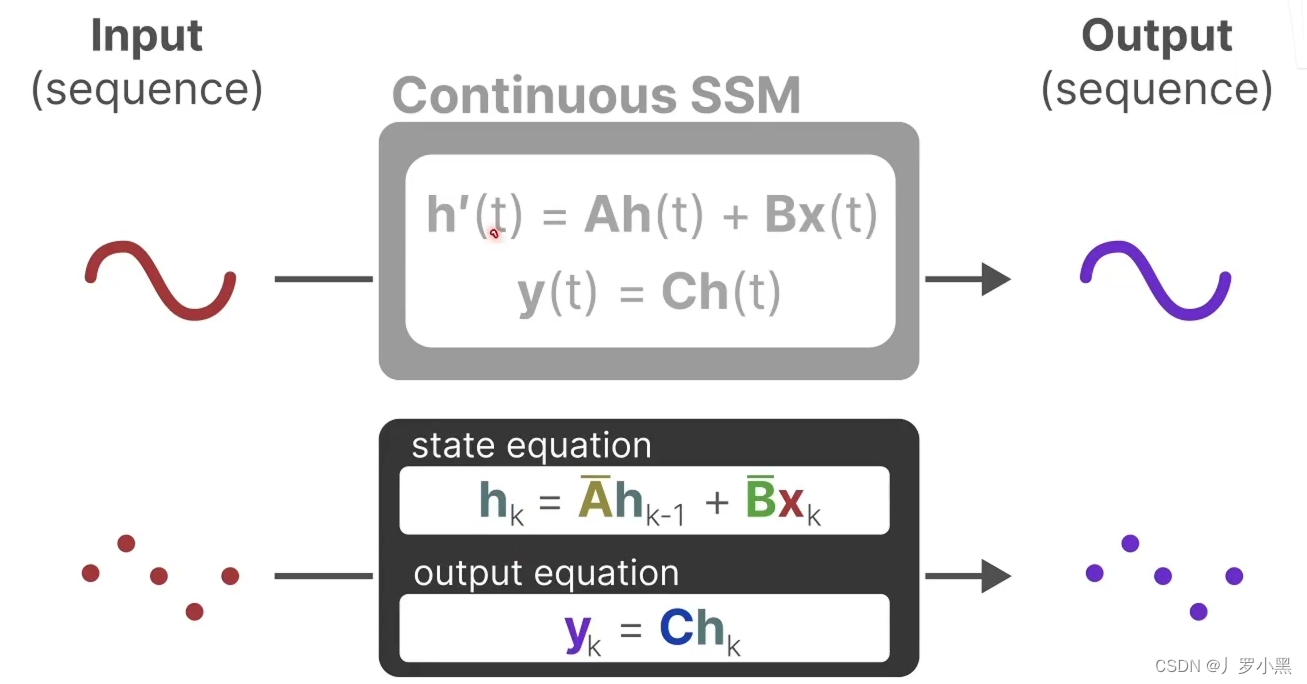
再看卷积结构表示，如下：
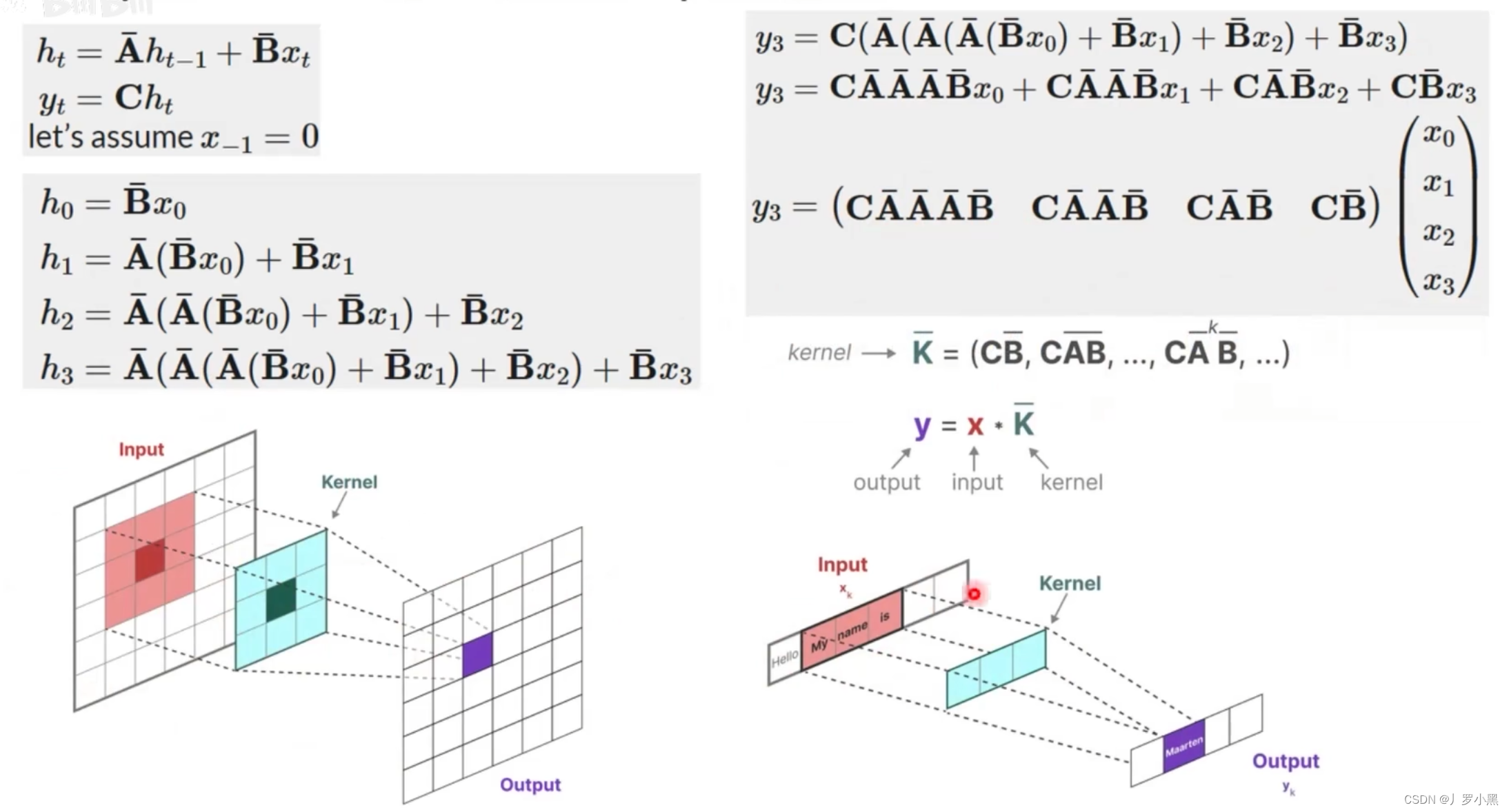
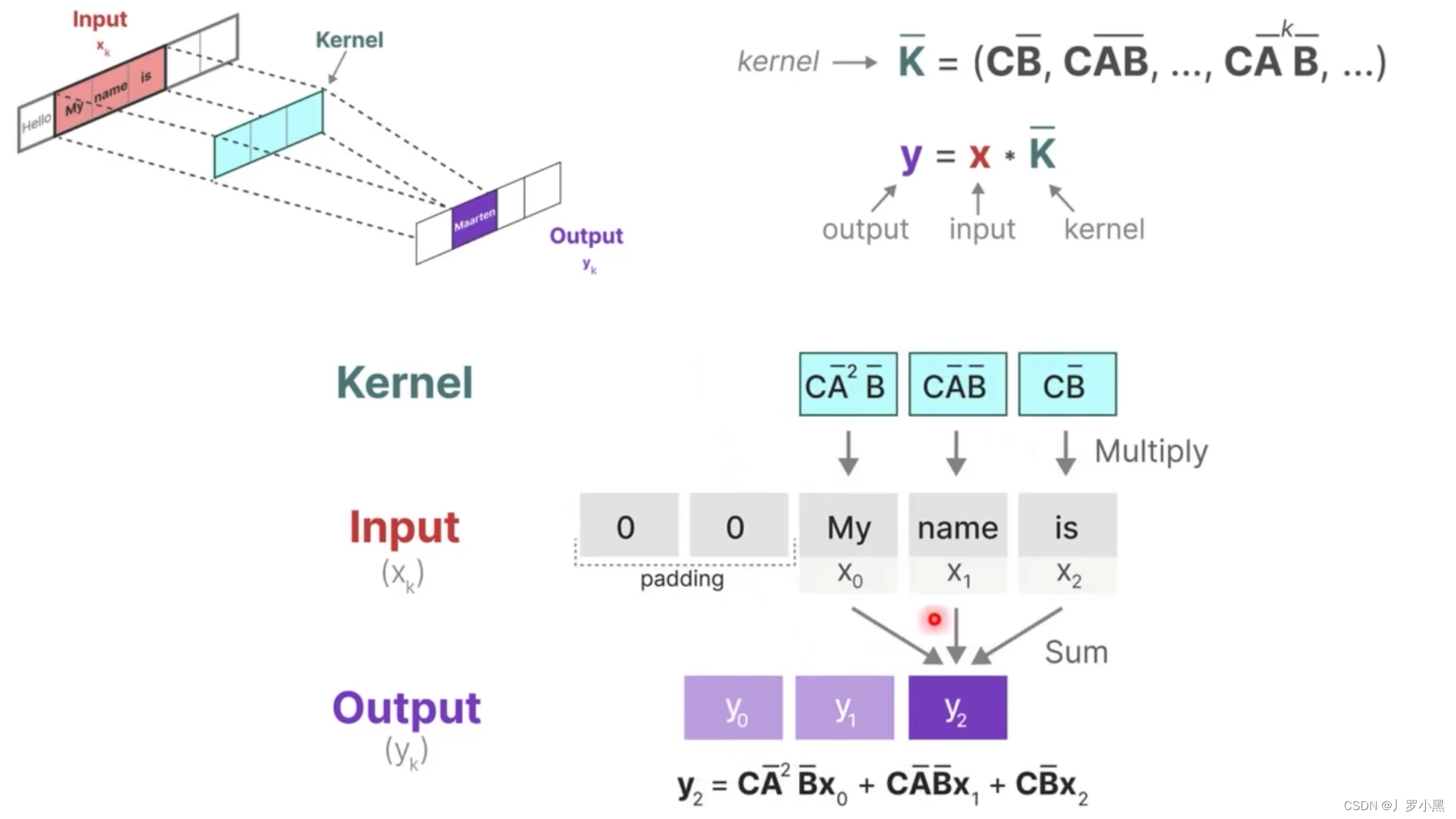
如果我们递归的将 $h_t$ 代入，并且展开可以得到一个 $h_t$ 的通用表达式，将这个表达式代回 $y_t$ 可以得到 $y_t$ 的通用表达式，而 $y_t$ 的表达式可以看作两个矩阵相乘，其中一个矩阵为输入矩阵（移动矩阵），另一个矩阵为固定矩阵（由于A、B、C矩阵是固定的，所以 $\overline{K}$ 也为固定矩阵），这个形式非常类似CNN中的卷积操作（但是由于mamba是处理文本的，所以只需要一维矩阵），而卷积可以并行，所以它也可以并行执行
注意：这里的输入矩阵并不是整个输入，而是对应于卷积上跟卷积核相乘的那个输入矩阵
由于我们之前说到SSM跟RNN很类似，于是S4还有一种循环表示形式，使用离散化的A、B矩阵后，如下：
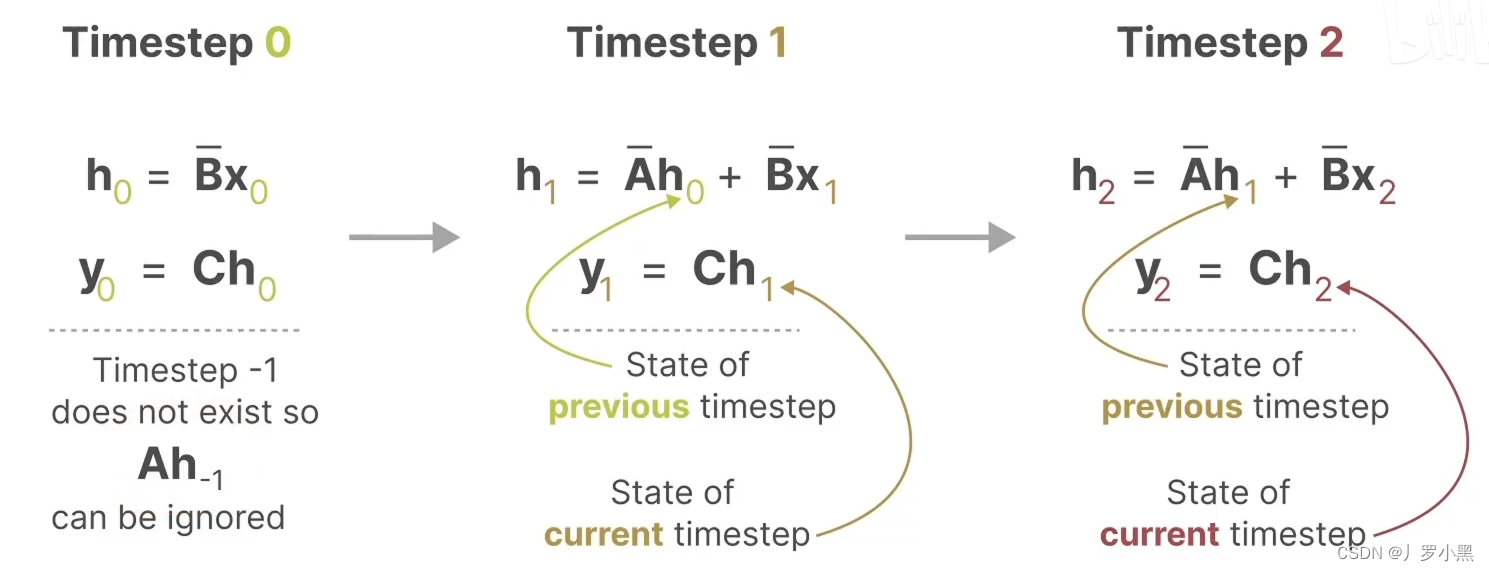
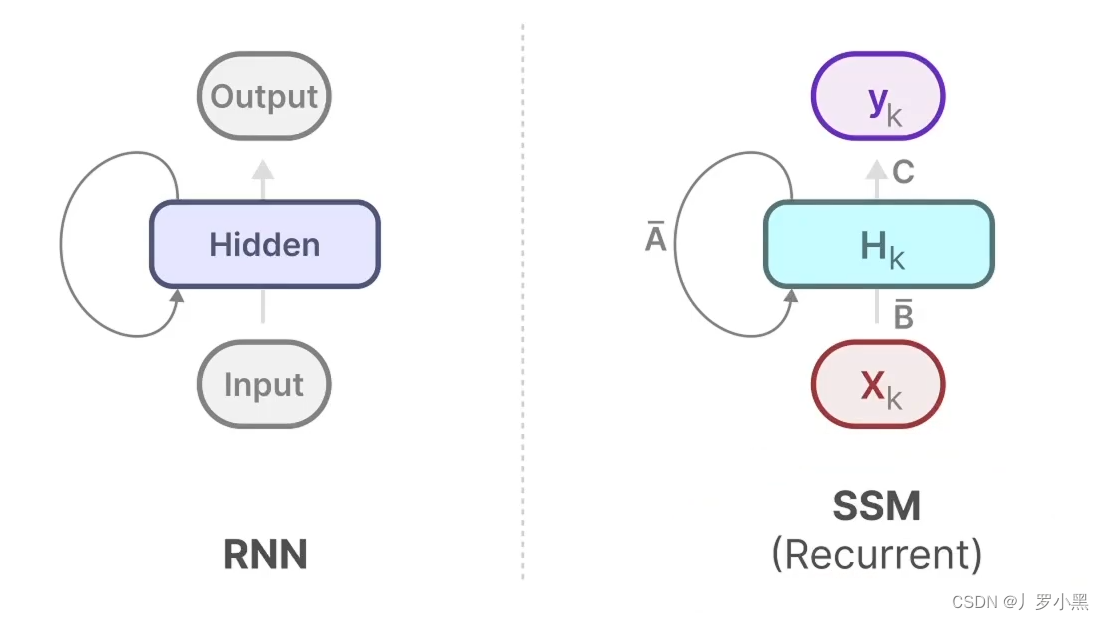
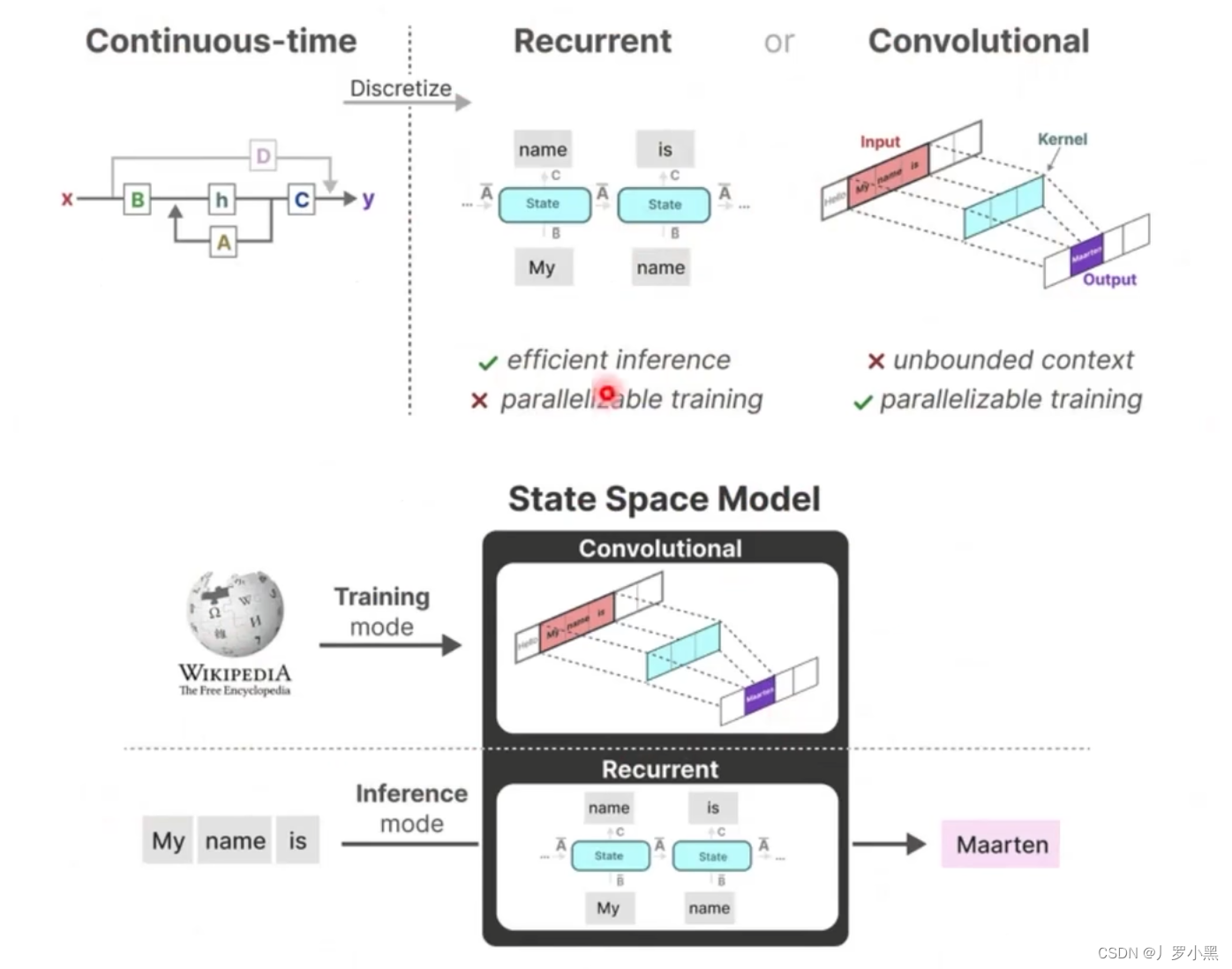
综上：S4模型有两种表示形式：循环表示类似RNN、卷积表示类似CNN。
那么我们可以在训练时使用CNN来进行并行计算，加快训练。在推理时使用RNN来直接生成预测结果，加快推理。
最后，我们看HIPPO矩阵，如下：
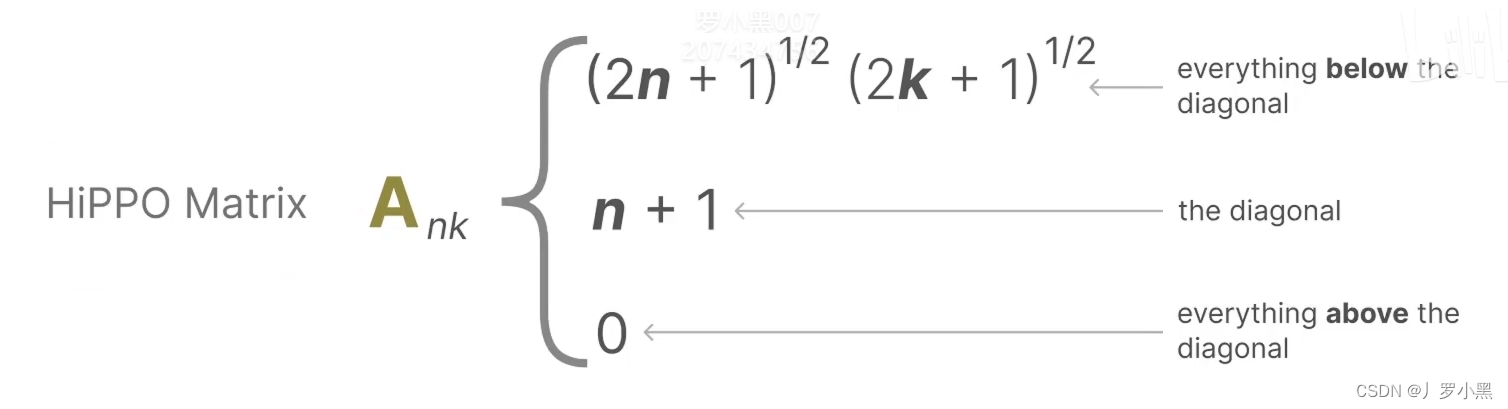
由于HIPPO矩阵也是一个二维矩阵，那么相比Transformer的注意力矩阵，并没有减少运算量，那么S4模型使用了低秩分解来表示HIPPO矩阵，从而减少运算量，如下：
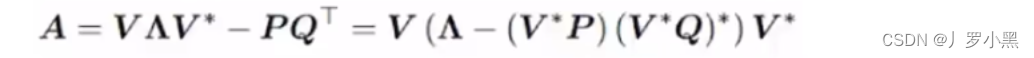
由于A矩阵是直接与状态相乘，所以使用HIPPO矩阵来替换掉之前SSM模型中的随机初始化的矩阵 $\overline{A}$ 。因为HIPPO矩阵能够很好的使用最近的token，并逐渐衰减较旧的token，如下：

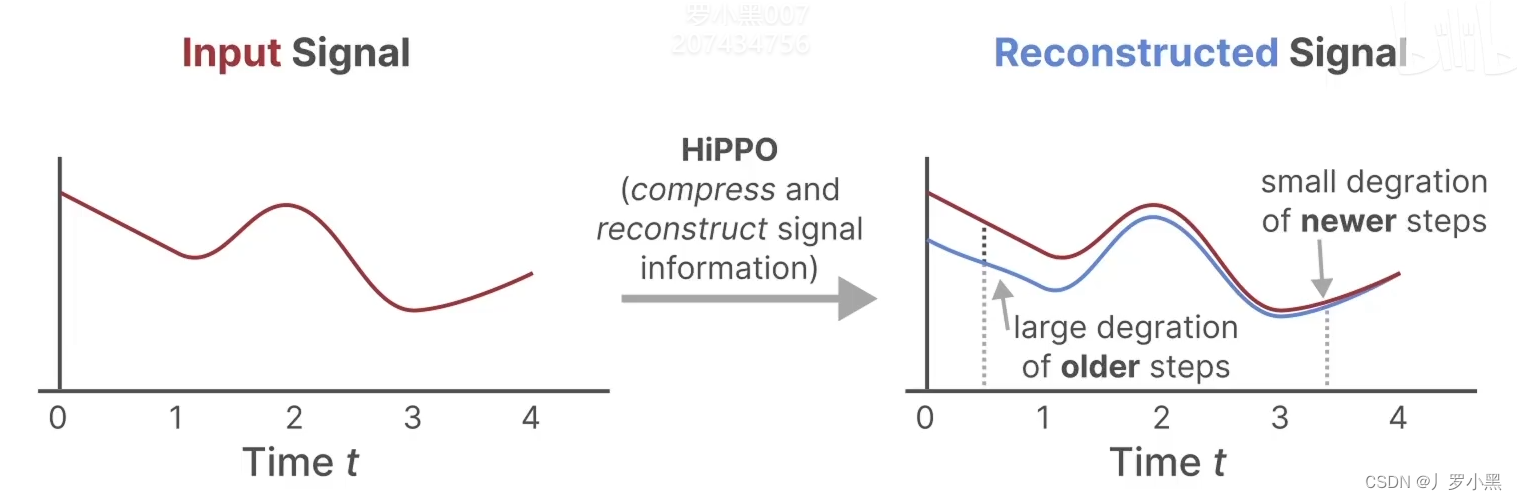
Mamba（S6）

Mamba模型对于S4模型的改进有以下三点：
1. 参数化矩阵：对输入信息进行有选择性的处理，从而得到类似Attention的效果，即不同的输入拥有不同的状态，token信息
2. 硬件感知算法，并行化–选择扫描算法，加快训练推理速度
3. 更简化的SSM模型架构
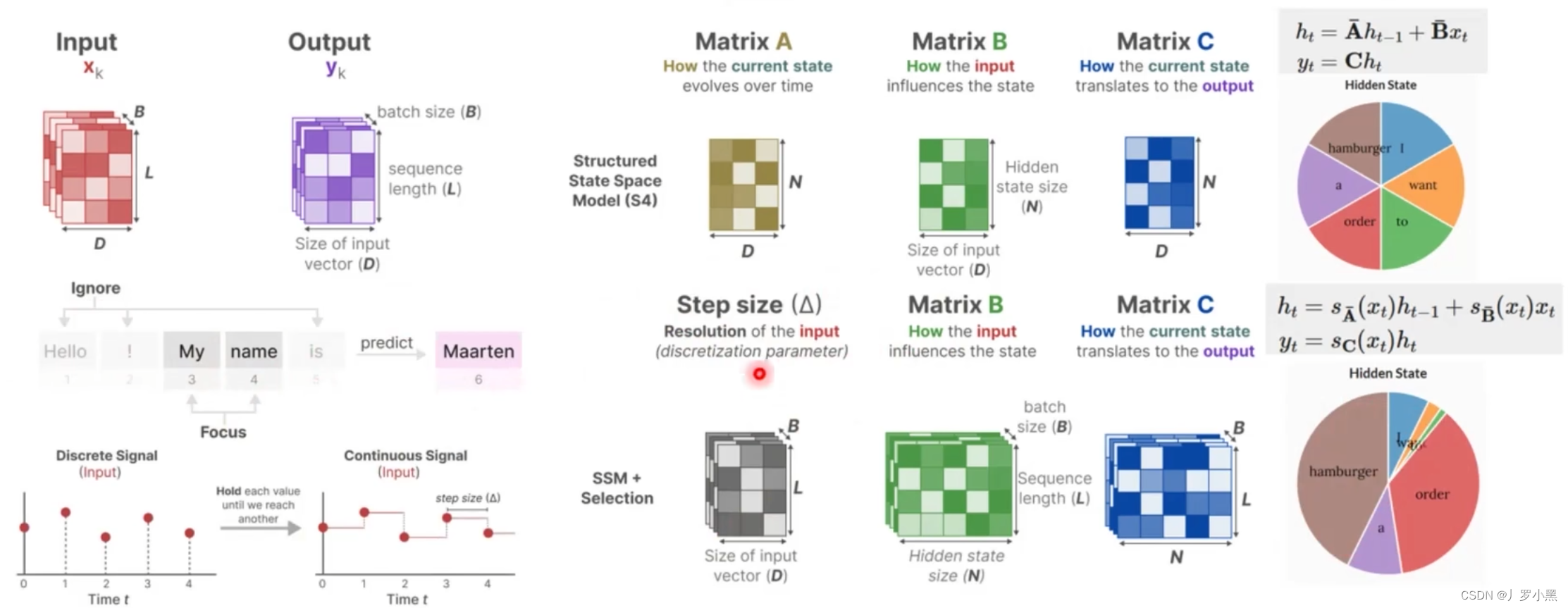
先看对输入信息进行有选择性的处理
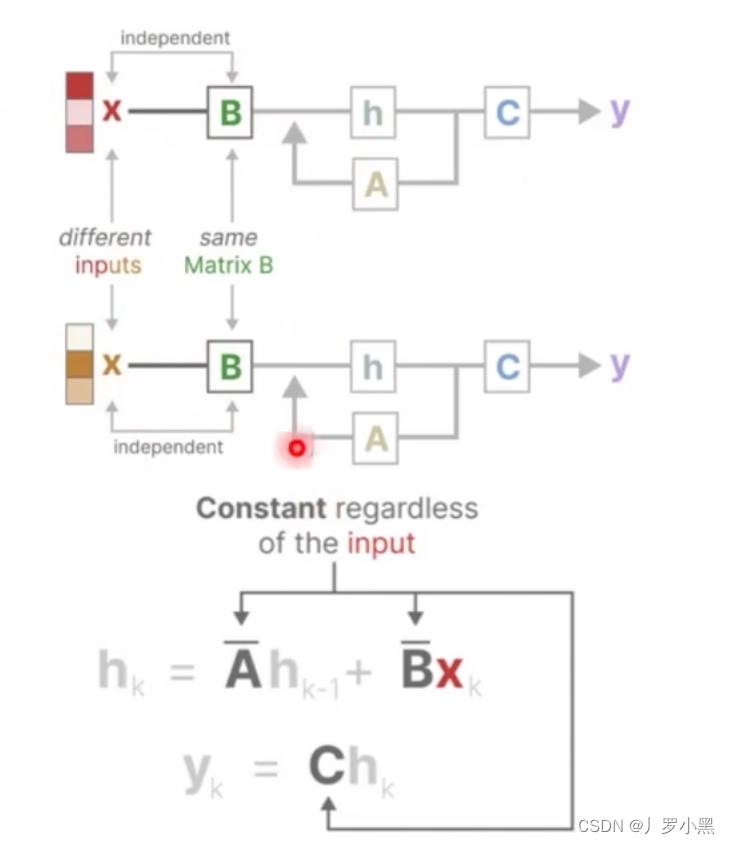
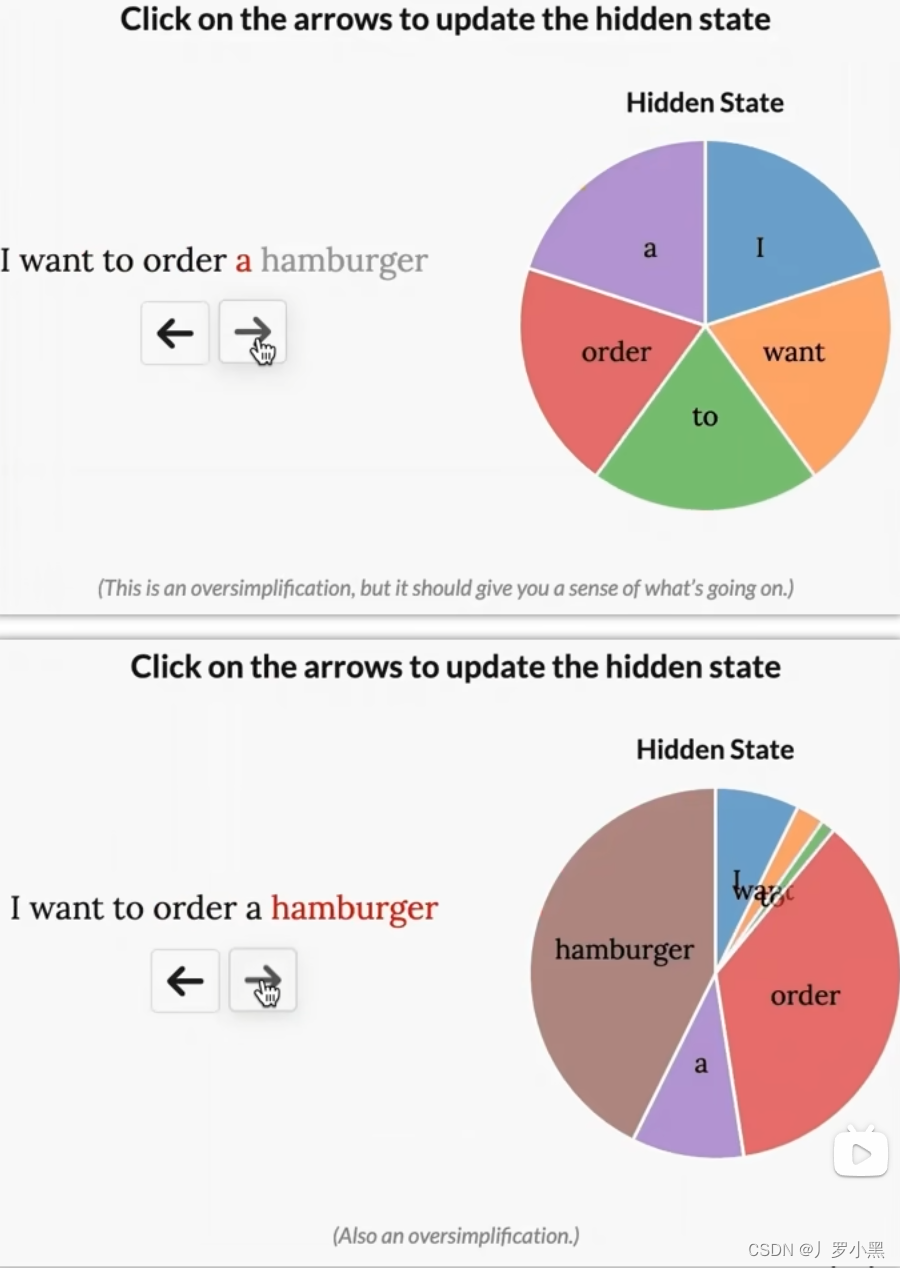
如上，A、B、C矩阵只会在训练过程中更新，一旦训练完成，在推理时，只要这个输入是模型没有见过的，那么对应的A、B矩阵都是完全一样的，这样会导致输入的状态信息也相同，没有针对性，不能做到像Attention那样，对于每个输入都有对应的注意力信息。
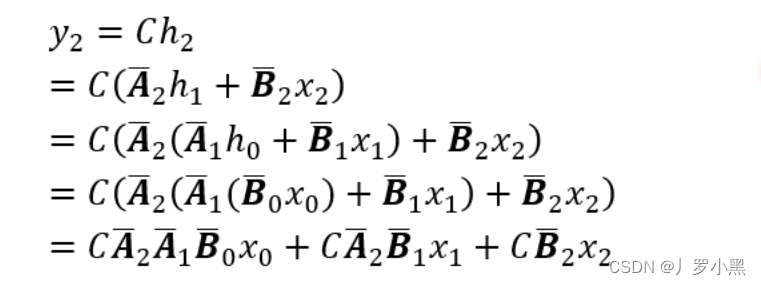
但是如果我们只是单单将A、B矩阵改为根据输入的变化而变化，那么由公式可以得出，只有当得到输入时，才能确定A、B矩阵，这样就无法像之前一样预先计算卷积核来进行并行加速运算了
这里Mamba模型采用了另外一种做法–参数矩阵，用来选择性的处理输入信息，如下：
B表示batch size，L表示序列长度，D为每个时间步 $\Delta$ 的数据特征维度，N表示状态的维度
Mamba使用了参数化矩阵，来让A、B、C矩阵能根据输入来进行对应的变化。在原始的S4模型中，在训练完成后，对于每个输入只有一个 $\overline{A}、\overline{B}$ 矩阵，但是在Mamba模型中，每个batch中的每个序列的每一个输入元素都有一个 $\overline{A}、\overline{B}$ 矩阵，如下：
注意：如果 $\Delta$ 越小，那么Mamba模型就会更关注之前时刻的状态，而忽略最近的状态，如果 $\Delta$ 越大，那么Mamba模型就会更关注最近的状态
接下来我们看，硬件感知算法，并行化–选择扫描算法：
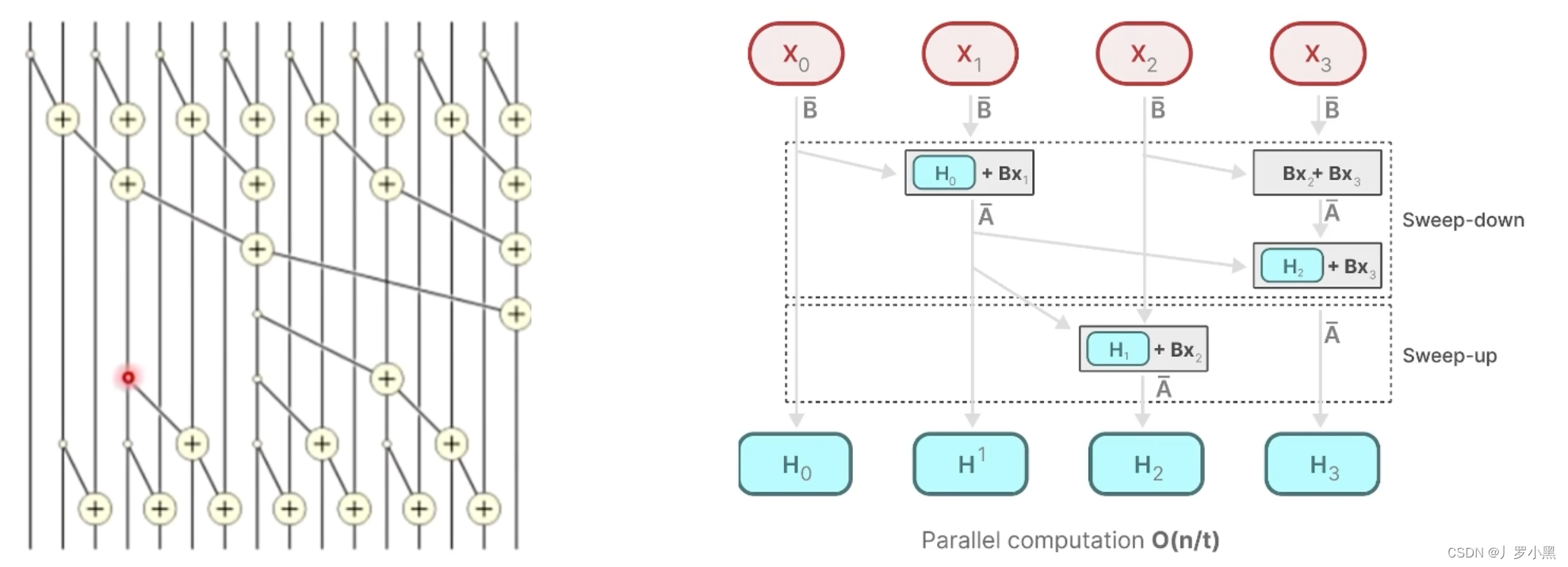
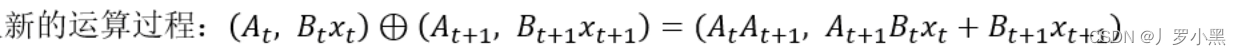
重新定义一种“加”运算，在这个运算中，是可以并行的，那么假设A矩阵是独立的，跟运算顺序是无关的，那么 $y_2$ 就可以表示为，如下：
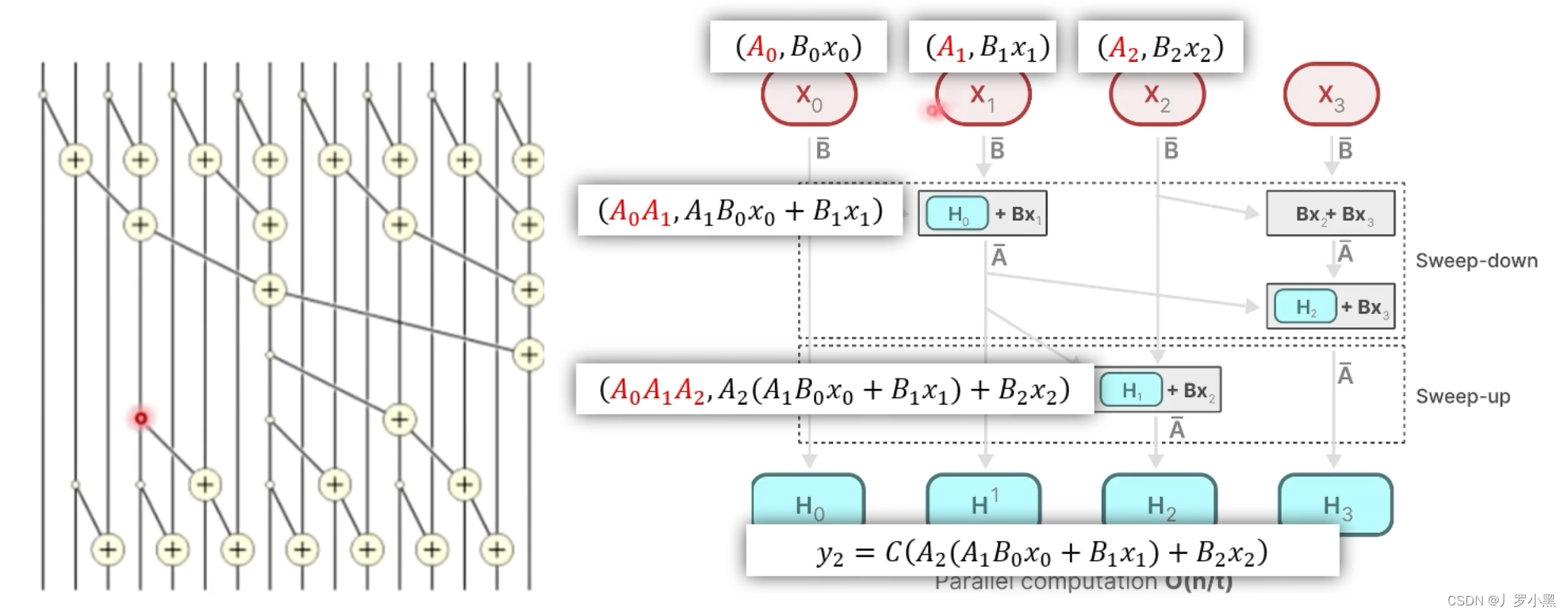
由上图可知，由于矩阵A是独立的，且B、C矩阵式通过x得到的，那么 $X_0$ “加” $X_1$ 取第二项就是 $H^1$ ， $X_0$ “加” $X_1$ 的结果再 “加” $X_2$ 取第二项就是 $H^2$ ，乘以C矩阵就是 $y_2$
对于计算 $y_3$ ，那么我们可以写出 $X_0、X_1、X_2、X_3$ 的新表示形式，然后分别计算第一层的结果，即 $X_0$ “加” $X_1$ 和 $X_2$ “加” $X_3$ 得到两个结果，再将这两个结果做"加"运算，将得到的结果取第二项，乘以C矩阵，就是 $y_3$ 的结果，如下：
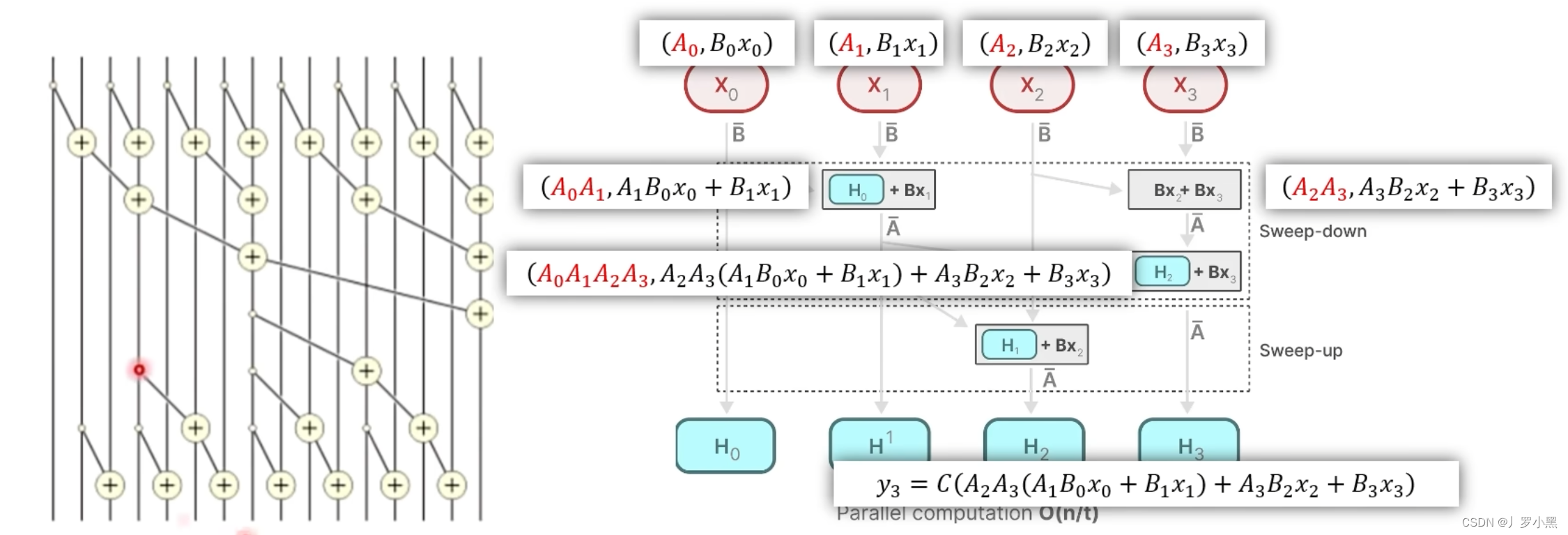
综上：使用了新定义的"加"运算可以并行操作，加快计算速度，解决了使用参数化矩阵后，无法使用卷积形式来加速运算的缺点
接下来我们看硬件感知算法：
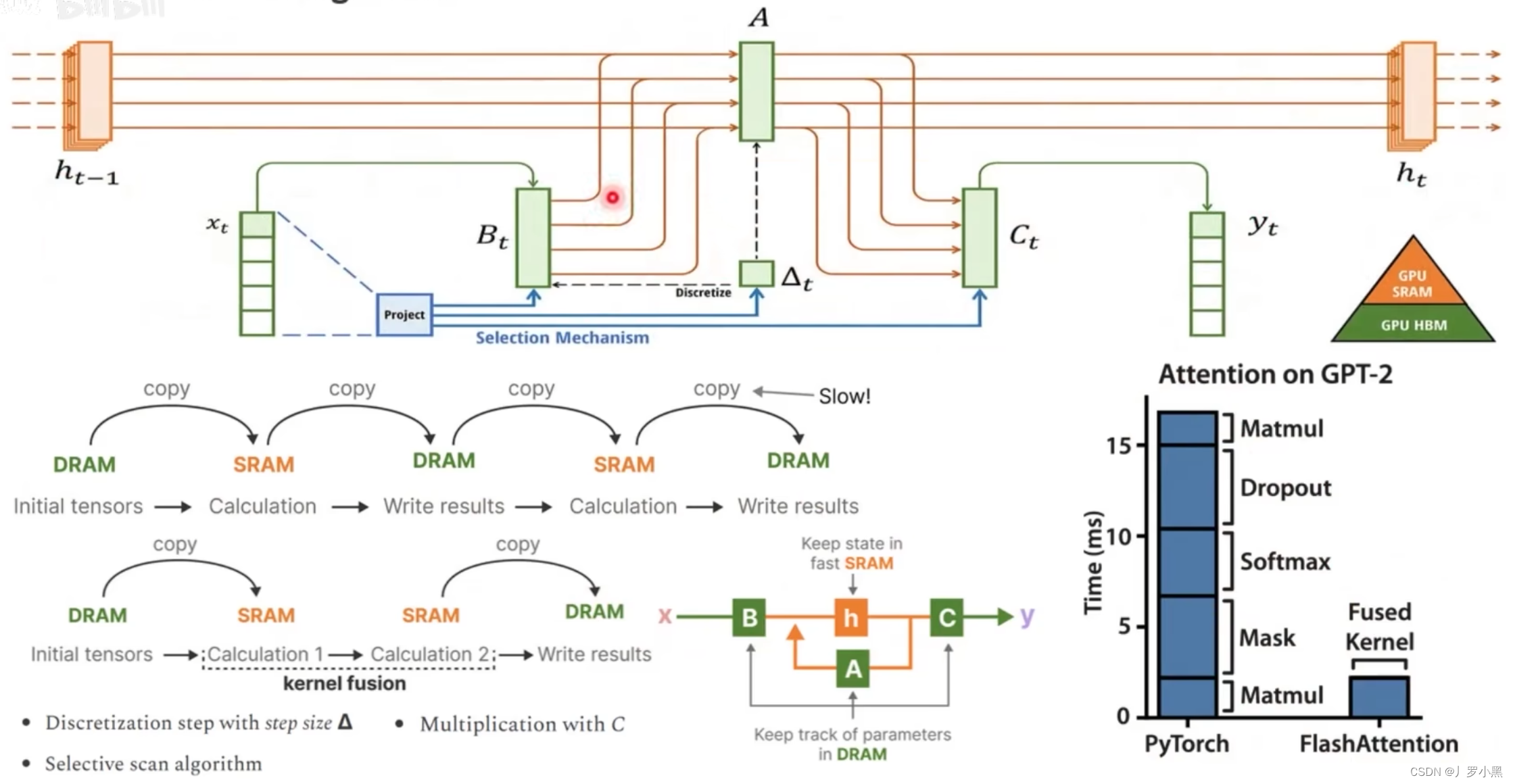
如上图，利用SSM本身显存占用小的优点，将重点状态更新的计算放在SRAM中，而其他的简单运算（A、B、C矩阵的获取等）都放到DRAM中。
而Transformer，由于显存占用过大，所以无法整个放入SRAM，只能从DRAM中分批放入SRAM，在计算完成后分批取出，这个来回存取的过程很浪费时间。
最后我们看Mamba提出的更简单的SSM结构，如下：
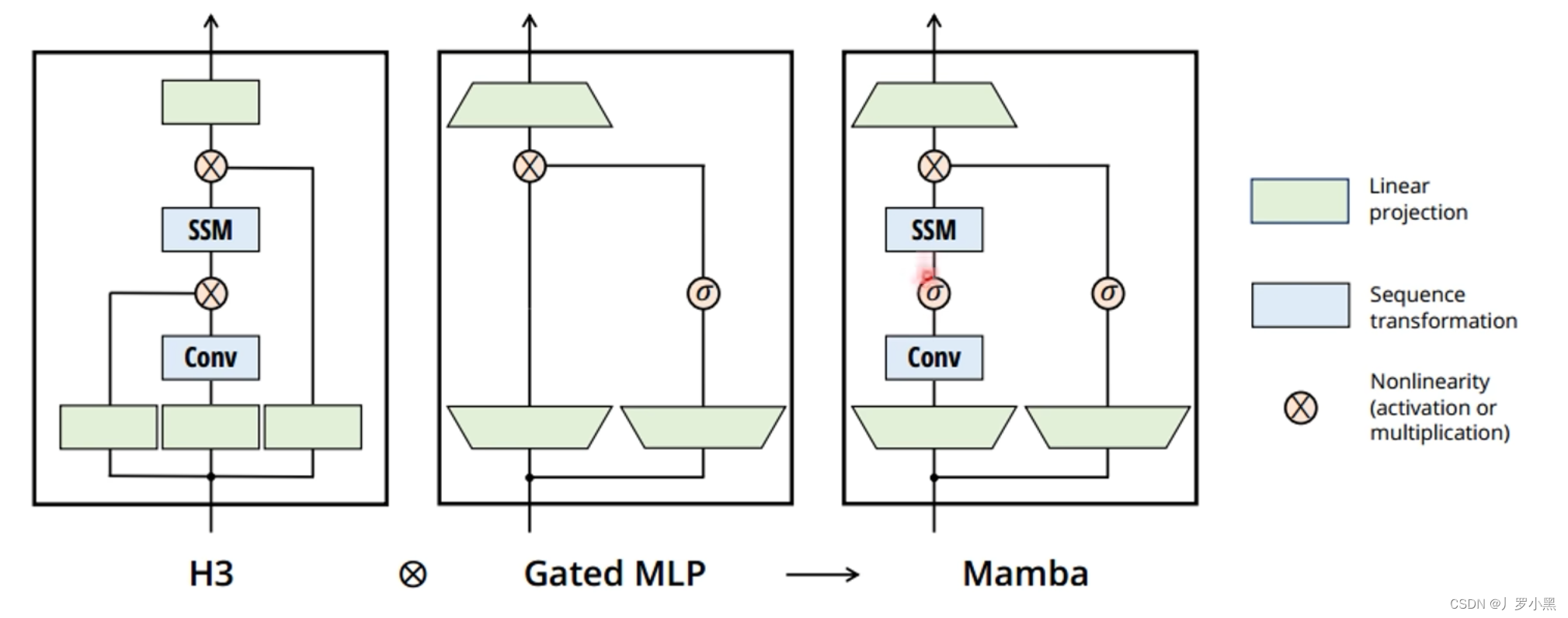
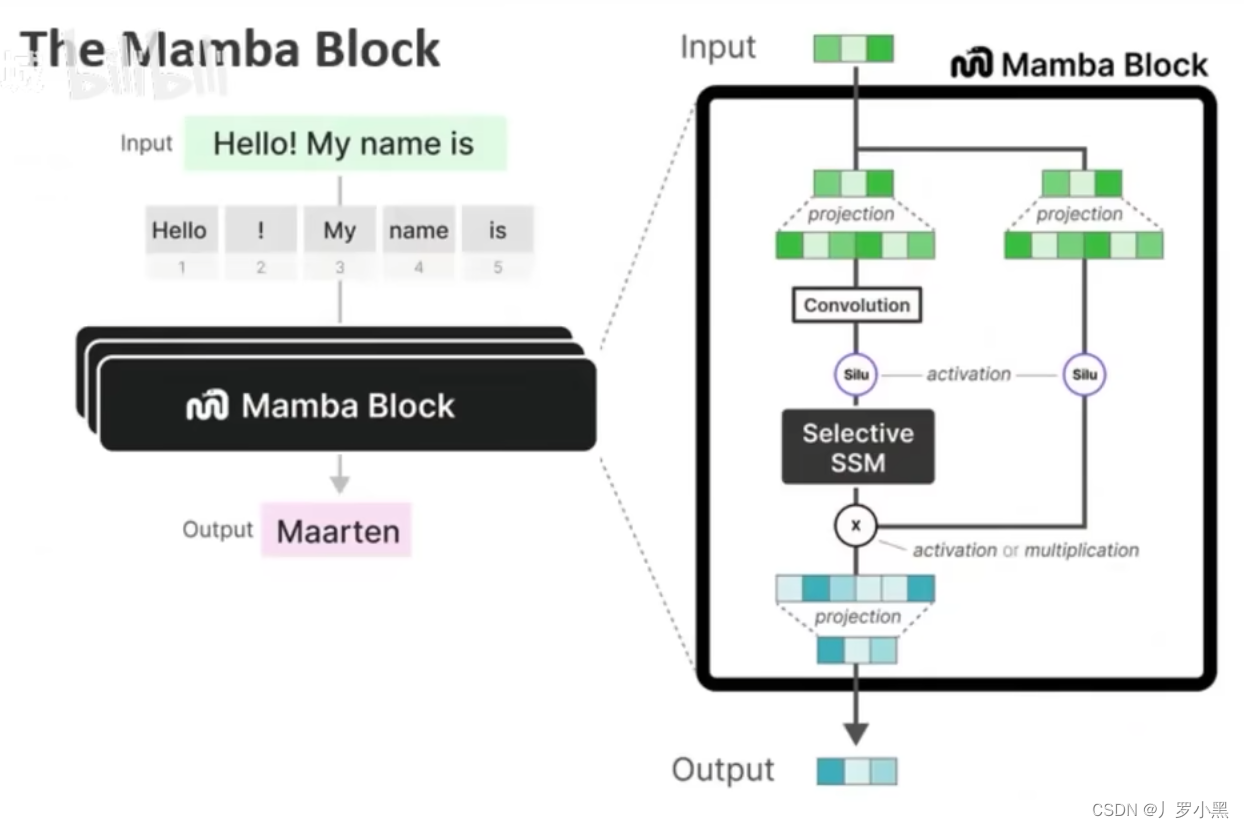
在上图中，输入信息会被分成两份：
1. 左侧会先进行线性嵌入，之后经过卷积、激活、SSM块（之前提到的并行计算就在卷积、SSM块中）
2. 右侧也会先进行线性嵌入，之后是一个门控，用于对信息进行筛选
3. 然后将左侧的结构乘以右侧的结果，再进行嵌入，通过一个跳跃连接，得到最后的输出

总结

Transformer、RNN、Mamba的对比如下：
对于CNN来说，训练时由于可以并行，所以训练速度也算快，但是推理的时候速度慢。但是由于Mamba没有使用卷积结构表示形式，而是定义了一种新的"加"运算，所以这里不拿CNN作为对比。
而Mamba就做到了，既克服了Transformer推理慢的缺点，也克服了RNN训练慢的缺点，解释如下：