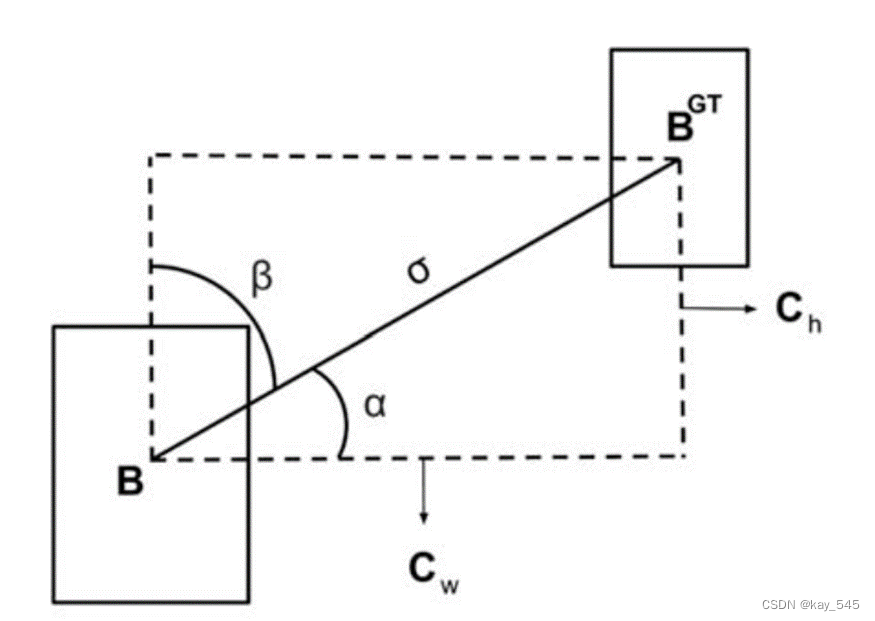
# encoding: utf-8
# 版权所有 2024 ©涂聚文有限公司
# 许可信息查看:
# 描述: https://github.com/Broham/suncalcPy
# Author : geovindu,Geovin Du 涂聚文.
# IDE : PyCharm 2023.1 python 3.11
# Datetime : 2024/5/14 21:59
# User : geovindu
# Product : PyCharm
# Project : EssentialAlgorithms
# File : sunCalc.py
# explain : 学习import math
from datetime import datetime, timedelta
import time
import calendarclass SunMoonTimeCalculator(object):"""日出日落,月升月落计算类"""def __init__(self):""""""self.PI = 3.141592653589793 # math.pi"""派"""self.sin = math.sin"""sin 函数"""self.cos = math.cos"""函数"""self.tan = math.tan"""函数"""self.asin = math.asin"""函数"""self.atan = math.atan2"""函数"""self.acos = math.acos"""函数"""self.rad = self.PI / 180.0self.e = self.rad * 23.4397 # obliquity of the Earthself.dayMs = 1000 * 60 * 60 * 24self.J1970 = 2440588self.J2000 = 2451545self.J0 = 0.0009self.times = [[-0.833, 'sunrise', 'sunset'],[-0.3, 'sunriseEnd', 'sunsetStart'],[-6, 'dawn', 'dusk'],[-12, 'nauticalDawn', 'nauticalDusk'],[-18, 'nightEnd', 'night'],[6, 'goldenHourEnd', 'goldenHour']]def rightAscension(self,l, b):""":param l::param b::return:"""return self.atan(self.sin(l) * self.cos(self.e) - self.tan(b) * self.sin(self.e), self.cos(l))def declination(self,l, b):""":param l::param b::return:"""return self.asin(self.sin(b) * self.cos(self.e) + self.cos(b) * self.sin(self.e) * self.sin(l))def azimuth(self,H, phi, dec):""":param H::param phi::param dec::return:"""return self.atan(self.sin(H), self.cos(H) * self.sin(phi) - self.tan(dec) * self.cos(phi))def altitude(self,H, phi, dec):""":param H::param phi::param dec::return:"""return self.asin(self.sin(phi) * self.sin(dec) + self.cos(phi) * self.cos(dec) * self.cos(H))def siderealTime(self,d, lw):""":param d::param lw::return:"""return self.rad * (280.16 + 360.9856235 * d) - lwdef toJulian(self,date):""":param date::return:"""return (time.mktime(date.timetuple()) * 1000) / self.dayMs - 0.5 + self.J1970def fromJulian(self,j):""":param j::return:"""return datetime.fromtimestamp(((j + 0.5 - self.J1970) * self.dayMs) / 1000.0)def toDays(self,date):""":param date::return:"""return self.toJulian(date) - self.J2000def julianCycle(self,d, lw):""":param d::param lw::return:"""return round(d - self.J0 - lw / (2 * self.PI))def approxTransit(self,Ht, lw, n):""":param Ht::param lw::param n::return:"""return self.J0 + (Ht + lw) / (2 * self.PI) + ndef solarTransitJ(self,ds, M, L):""":param ds::param M::param L::return:"""return self.J2000 + ds + 0.0053 * self.sin(M) - 0.0069 * self.sin(2 * L)def hourAngle(self,h, phi, d):""":param h::param phi::param d::return:"""try:ret = self.acos((self.sin(h) - self.sin(phi) * self.sin(d)) / (self.cos(phi) * self.cos(d)))return retexcept ValueError as e:print(h, phi, d, "=>", e)def observerAngle(self,height):""":param height::return:"""return -2.076 * math.sqrt(height) / 60def solarMeanAnomaly(self,d):""":param d::return:"""return self.rad * (357.5291 + 0.98560028 * d)def eclipticLongitude(self,M):""":param M::return:"""C = self.rad * (1.9148 * self.sin(M) + 0.02 * self.sin(2 * M) + 0.0003 * self.sin(3 * M)) # equation of centerP = self.rad * 102.9372 # perihelion of the Earthreturn M + C + P + self.PIdef sunCoords(self,d):""":param d::return:"""M = self.solarMeanAnomaly(d)L = self.eclipticLongitude(M)return dict(dec=self.declination(L, 0),ra=self.rightAscension(L, 0))def getSetJ(self,h, lw, phi, dec, n, M, L):""":param h::param lw::param phi::param dec::param n::param M::param L::return:"""w = self.hourAngle(h, phi, dec)a = self.approxTransit(w, lw, n)return self.solarTransitJ(a, M, L)def moonCoords(self,d):"""geocentric ecliptic coordinates of the moon:param d::return:"""L = self.rad * (218.316 + 13.176396 * d)M = self.rad * (134.963 + 13.064993 * d)F = self.rad * (93.272 + 13.229350 * d)l = L + self.rad * 6.289 * self.sin(M)b = self.rad * 5.128 * self.sin(F)dt = 385001 - 20905 * self.cos(M)return dict(ra=self.rightAscension(l, b),dec=self.declination(l, b),dist=dt)def getMoonIllumination(self,date):"""Gets illumination properties of the moon for the given time.:param date::return:"""d = self.toDays(date)s = self.sunCoords(d)m = self.moonCoords(d)# distance from Earth to Sun in kmsdist = 149598000phi = self.acos(self.sin(s["dec"]) * self.sin(m["dec"]) + self.cos(s["dec"]) * self.cos(m["dec"]) * self.cos(s["ra"] - m["ra"]))inc = self.atan(sdist * self.sin(phi), m["dist"] - sdist * self.cos(phi))angle = self.atan(self.cos(s["dec"]) * self.sin(s["ra"] - m["ra"]),self.sin(s["dec"]) * self.cos(m["dec"]) - self.cos(s["dec"]) * self.sin(m["dec"]) * self.cos(s["ra"] - m["ra"]))return dict(fraction=(1 + self.cos(inc)) / 2,phase=0.5 + 0.5 * inc * (-1 if angle < 0 else 1) / self.PI,angle=angle)def getSunrise(self,date, lat, lng):""":param lat::param lng::return:"""ret = self.getTimes(date, lat, lng)return ret["sunrise"]def getTimes(self,date, lat, lng, height=0):"""Gets sun rise/set properties for the given time, location and height.:param date::param lat::param lng::param height::return:"""lw = self.rad * -lngphi = self.rad * latdh = self.observerAngle(height)d = self.toDays(date)n = self.julianCycle(d, lw)ds = self.approxTransit(0, lw, n)M = self.solarMeanAnomaly(ds)L = self.eclipticLongitude(M)dec = self.declination(L, 0)Jnoon = self.solarTransitJ(ds, M, L)result = dict(solarNoon=self.fromJulian(Jnoon).strftime('%Y-%m-%d %H:%M:%S'),nadir=self.fromJulian(Jnoon - 0.5).strftime('%Y-%m-%d %H:%M:%S'))for i in range(0, len(self.times)):time = self.times[i]h0 = (time[0] + dh) * self.radJset = self.getSetJ(h0, lw, phi, dec, n, M, L)Jrise = Jnoon - (Jset - Jnoon)result[time[1]] = self.fromJulian(Jrise).strftime('%Y-%m-%d %H:%M:%S')result[time[2]] = self.fromJulian(Jset).strftime('%Y-%m-%d %H:%M:%S')return resultdef hoursLater(self,date, h):""":param date::param h::return:"""return date + timedelta(hours=h)def getMoonTimes(self,date, lat, lng):""":param date::param lat::param lng::return:""""""Gets moon rise/set properties for the given time and location."""t = date.replace(hour=0, minute=0, second=0)hc = 0.133 * self.radh0 = self.getMoonPosition(t, lat, lng)["altitude"] - hcrise = 0sett = 0# go in 2-hour chunks, each time seeing if a 3-point quadratic curve crosses zero (which means rise or set)for i in range(1, 25, 2):h1 = self.getMoonPosition(self.hoursLater(t, i), lat, lng)["altitude"] - hch2 = self.getMoonPosition(self.hoursLater(t, i + 1), lat, lng)["altitude"] - hca = (h0 + h2) / 2 - h1b = (h2 - h0) / 2xe = -b / (2 * a)ye = (a * xe + b) * xe + h1d = b * b - 4 * a * h1roots = 0if d >= 0:dx = math.sqrt(d) / (abs(a) * 2)x1 = xe - dxx2 = xe + dxif abs(x1) <= 1:roots += 1if abs(x2) <= 1:roots += 1if x1 < -1:x1 = x2if roots == 1:if h0 < 0:rise = i + x1else:sett = i + x1elif roots == 2:rise = i + (x2 if ye < 0 else x1)sett = i + (x1 if ye < 0 else x2)if (rise and sett):breakh0 = h2result = dict()if (rise):result["rise"] = self.hoursLater(t, rise)if (sett):result["set"] = self.hoursLater(t, sett)if (not rise and not sett):value = 'alwaysUp' if ye > 0 else 'alwaysDown'result[value] = Truereturn resultdef getMoonPosition(self,date, lat, lng):"""Gets positional attributes of the moon for the given time and location.:param date::param lat::param lng::return:"""lw = self.rad * -lngphi = self.rad * latd = self.toDays(date)c = self.moonCoords(d)H = self.siderealTime(d, lw) - c["ra"]h = self.altitude(H, phi, c["dec"])# altitude correction for refractionh = h + self.rad * 0.017 / self.tan(h + self.rad * 10.26 / (h + self.rad * 5.10))pa = self.atan(self.sin(H), self.tan(phi) * self.cos(c["dec"]) - self.sin(c["dec"]) * self.cos(H))return dict(azimuth=self.azimuth(H, phi, c["dec"]),altitude=h,distance=c["dist"],parallacticAngle=pa)def getPosition(self,date, lat, lng):"""Returns positional attributes of the sun for the given time and location.:param date::param lat::param lng::return:"""lw = self.rad * -lngphi = self.rad * latd = self.toDays(date)c = self.sunCoords(d)H = self.siderealTime(d, lw) - c["ra"]# print("d", d, "c",c,"H",H,"phi", phi)return dict(azimuth=self.azimuth(H, phi, c["dec"]),altitude=self.altitude(H, phi, c["dec"]))调用:
#日出日落 深圳
sun=Common.sunCalc.SunMoonTimeCalculator()
lat= 22.5445741
lng= 114.0545429
print(sun.getTimes(datetime.now(), lat, lng))
print(sun.getMoonIllumination(datetime.now()))
#月升月落
print(sun.getMoonTimes(datetime.now(), lat, lng))输出: