6.2.2 快速排序
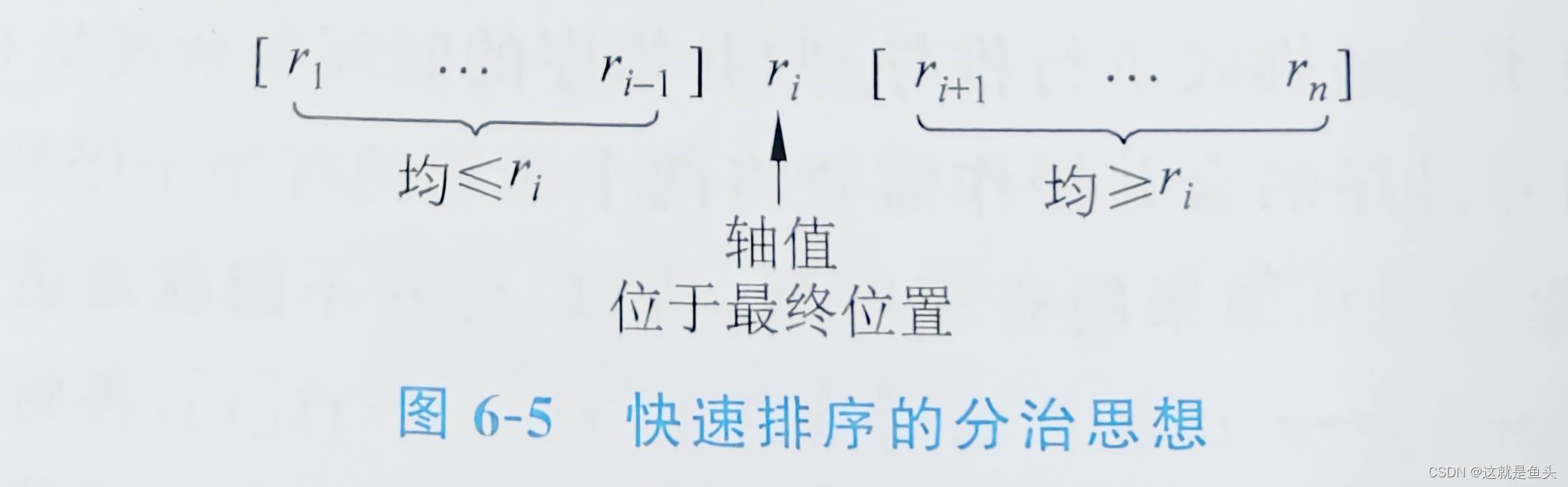
【问题】快速排序(quick sort)的分治策略如下(图6-5)。
(1)划分:(选定一个记录作为轴值,以轴值为基准将整个序列划分为两个子序列,轴值的位置在划分的过程中确定,并且左侧子序列的所有记录均小于或等于轴值,右侧子序列的所有记录均大于或等于轴值。
(2) 求解子问题:分别对划分后的每一个子序列进行递归处理。
(3) 合并:由于对子序列的排序是就地进行的,所以合并不需要执行任何操作。
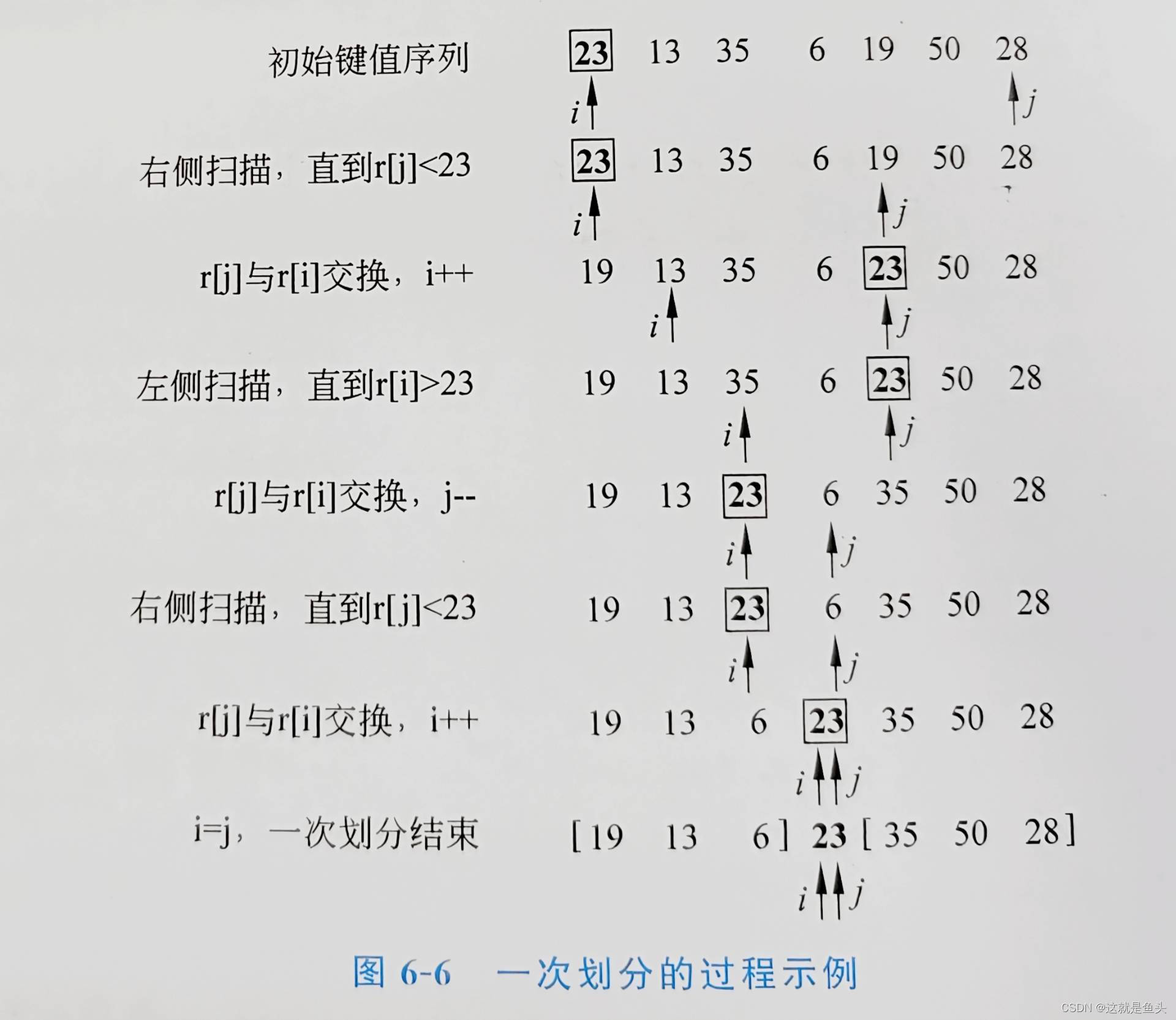
【想法】首先对待排序记录序列进行划分,刻分的轴值应该遵循平衡子问题的原则,使划分后两个子序列的长度尽量相等。轴值的选择有很多方法,例如,可以随机选出一个记录作为轴值,从而期望划分是较平衡的。假设以第一个记录作为轴值,图6-6给出了、个划分的例子(黑体框代表轴值)。
以轴值为基准将待排序序列划分为两个子序列后,对每一个子序列分别进行递归处理。图6-7所示是一个快速排序的完整的例子。

【算法实现】设函数Partition实现对序列r[first]~r[end]进行划分,函数QuickSort实现快速排序,程序如下。
#include <iostream>
using namespace std;
int Partition(int r[ ], int first, int end)
{
int temp, i = first, j = end;
while (i < j)
{
while (i < j && r[i] <= r[j]) j--; //右侧扫描
if (i < j)
{
temp = r[i]; r[i] = r[j]; r[j] = temp; //将较小记录交换到前面
i++;
}
while (i < j && r[i] <= r[j]) i++; //左侧扫描
if (i < j)
{
temp = r[i]; r[i] = r[j]; r[j] = temp; //将较大记录交换到后面
j--;
}
}
return i; //返回轴值记录的位置
}
void QuickSort(int r[ ], int first, int end) //快速排序
{
if (first < end)
{
int pivot = Partition(r, first, end); //划分,pivot是轴值的位置
QuickSort(r, first, pivot-1); //对左侧子序列进行快速排序
QuickSort(r, pivot+1, end); //对右侧子序列进行快速排序
}
}
int main( )
{
int i, n = 8, r[8] = {8,3,2,6,7,1,5,4};
QuickSort(r, 0, n-1);
for (i = 0; i < n; i++)
std::cout << r[i] << " "; // 打印排序后的元素
std::cout << std::endl;
return 0;
}
【算法分析】 最好情况下,每次划分对一个记录定位后,该记录的左侧子序列与右侧子序列的长度相同。在具有n个记录的序列中,一次划分需要对整个待划分序列扫描一遍,所需时间为O(n),则有:
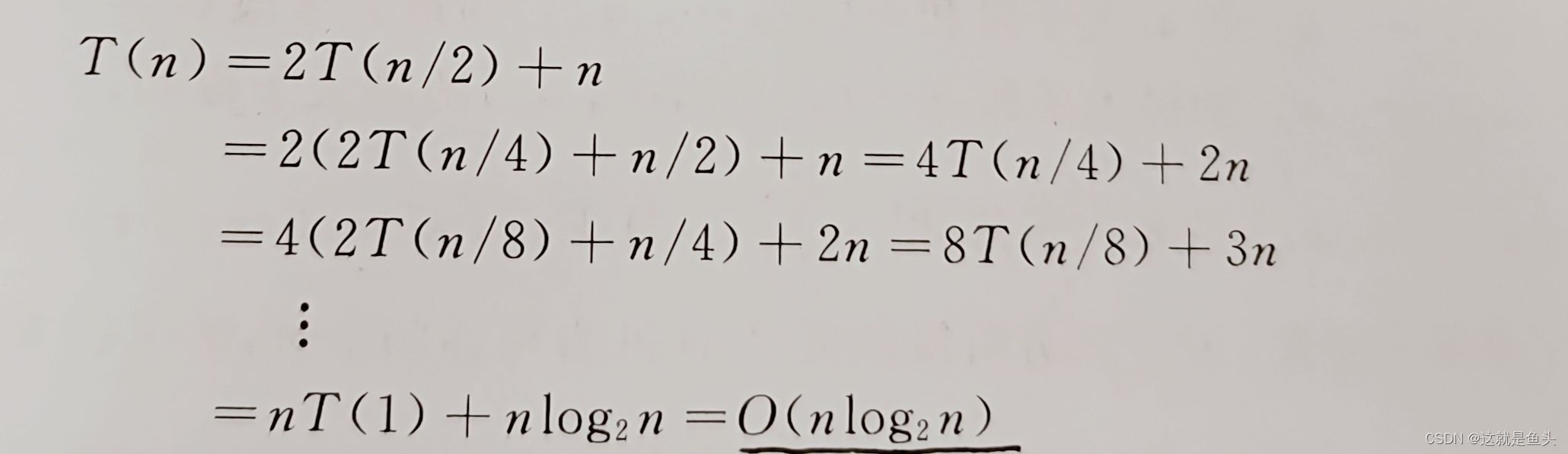
最坏情况下,待排序记录序列正序或逆序,每次划分只得到一个比上一次划分少一个记录的子序列(另一个子序列为空)。此时,必须经过n-1次递归调用才能把所有记录定位,而且第i趟划分需要经过n-i次比较才能找到第i个记录的位置,因此,时间复杂度为:
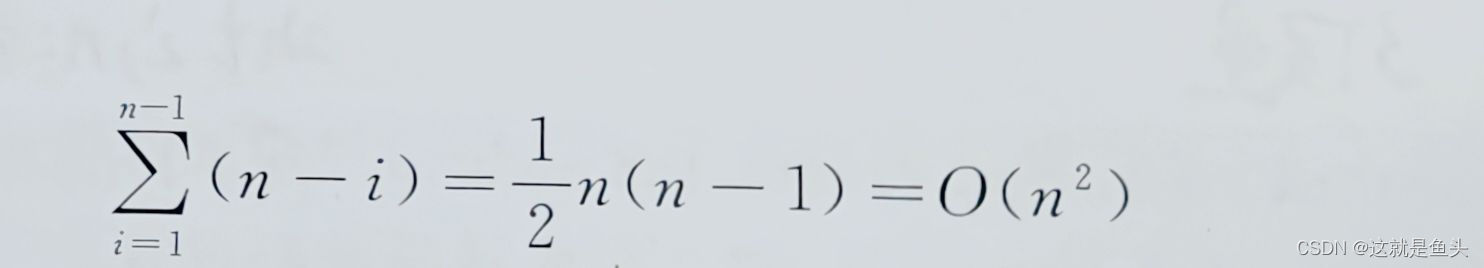
平均情况下,设轴值记录的关键码第k小(1<=k<=n),则有: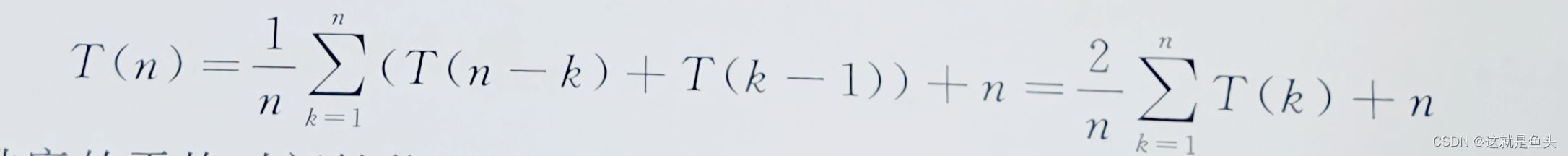
这是快速排序的平均时间性能,可以用归纳法证明,其数量级也为O(nlog以2为底n)。
由于快速排序是递归执行的,需要一个工作栈来存放每一层递归调用的必要信息,栈
的最大容量与递归调用的深度一致。最好情况下要进行[log以2为底n]次递归调用,栈的深度为O(log,n);最坏情况下,要进行n-1次递归调用,栈的深度为O(n);平均情况下,栈的深度为O(log以2为底n).
6.3.1 最大子段和问题

应用实例
国际期货市场某种商品在某个月的第1,2,...,31天的价格涨幅分别记为a1, a2,...,a31,若某天的价格下跌,这天的涨幅就是负值。如果想知道在连续哪些天,该商品的价格具有最高涨幅,究竟涨了多少,这个问题就可以抽象为最大子段和问题。


【算法实现】 最大子段和问题是按照位置进行划分的,设变量 center 表示序列的中间位置,数组a[n]存放整数序列,程序如下。
#include <iostream>
using namespace std;
int MaxSum(int a[ ], int left, int right)
{
int sum = 0, midSum = 0, leftSum = 0, rightSum = 0;
int i, center, s1, s2, lefts, rights;
if (left == right) //如果序列长度为1,直接求解
sum = a[left];
else
{
center = (left + right)/2; //划分
leftSum = MaxSum(a, left, center); //对应情况①,递归求解
rightSum = MaxSum(a, center+1, right); //对应情况②,递归求解
s1 = 0; lefts = 0; //以下对应情况③,先求解s1
for (i = center; i >= left; i--)
{
lefts += a[i];
if (lefts > s1) s1 = lefts;
}
s2 = 0; rights = 0; //再求解s2
for (i = center + 1; i <= right; i++)
{
rights += a[i];
if (rights > s2) s2 = rights;
}
midSum = s1 + s2; //计算情况③的最大子段和
if (midSum < leftSum) sum = leftSum; //合并解,取较大者
else sum = midSum;
if (sum < rightSum) sum = rightSum;
}
return sum;
}
int main( )
{
int max, n = 6, r[6] = {-20, 11, -4, 13, -5, -2};
max = MaxSum(r, 0, n - 1);
cout << "最大子段和是:" << max << endl;
return 0;
}