数据结构之栈与队列

一.栈

1.定义：一种线性表，只允许在固定的一端进行删除和插入数据的操作，该端叫栈底，另一端叫栈顶

2.特点：先进后出

注：栈中元素出栈是一对多的(他虽然满足先进后出但是我们可以在pop数据前先获取栈顶元素并打印再pop，这样就可能改变数据在屏幕上出现的顺序)

3.思路：可以用数组实现，也可以用链表实现

数组实现更简单，链表实现较为复杂，下面小编将从两方面解释不选择链表实现的原因

1>若选择单链表，在进行删除操作时，我们不好解决栈顶先前移一位的问题

2>若选择双向链表，将占用过多的内存

4.代码实现(以数组实现栈为例)：

(1)栈的结构体定义：包含数组指针，栈顶的位置，有效空间容量

typedef int STDatatype;
typedef struct Stack
{STDatatype* arr;int top;//栈顶int capacity;//有效空间容量
}ST;

(2)栈的初始化：将栈顶初始化为0：表示栈顶指向最后一个数据的下一个

                          将栈顶初始化为-1：表示栈顶指向最后一个数据所在位置

//栈的初始化
void STInit(ST* ps)
{assert(ps);ps->arr = NULL;//top指向栈顶后的一个元素,此时top等值于有效数据个数ps->top = 0;ps->capacity = 0;
}

(3)栈的销毁

//栈的销毁
void STDestory(ST* ps)
{assert(ps);free(ps->arr);ps->arr = NULL;ps->capacity = ps->top = 0;
}

(4)插入数据/入栈：先判断是否需要增容，再插入数据

//入栈
void STPush(ST* ps, STDatatype x)
{assert(ps);//判断是否需要增容if (ps->top == ps->capacity){int newcapacity = ps->capacity * 2==0 ? 4 : ps->capacity*2;STDatatype* tmp = (STDatatype*)realloc(ps->arr, sizeof(STDatatype) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}ps->arr = tmp;ps->capacity = newcapacity;}ps->arr[ps->top] = x;ps->top++;
}

(5)删除数据/出栈：先判断数组是否为空，再将top--即完成删除

//出栈
void STPop(ST* ps)
{assert(ps);assert(ps->top > 0);ps->top--;
}

(6)获取栈顶元素

//获取栈顶数据
STDatatype STTop(ST* ps)
{assert(ps);return ps->arr[ps->top-1];
}

(7)判断栈是否为空：若top==0则为空

//判断栈是否为空
bool STEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}

(8)栈中有效数据个数

//栈的有效数据个数
int STSize(ST* ps)
{assert(ps);return ps->top;
}

二.队列

1.定义：一种线性表，只允许在一端(队尾)进行数据插入，在另一端(队头)进行数据删除

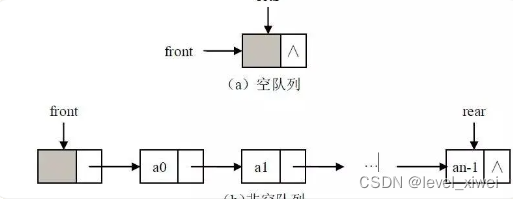
2.特点：先进先出

注：队列的数据出队列时是一对一的

3.思路：可以用数组实现，也可以用链表实现 

单链表实现更简单，数组实现较为复杂，是因为在使用数组实现时，进行删除数据不好记录下一次该删除数据的位置

4.代码实现(以单链表实现队列为例)：

(1)队列的节点定义：指向下一个节点的指针，存储数据的数值

    队列的结构体定义：队列的头指针，尾指针，队列有效数据的个数

typedef int QueueDataType;typedef struct QueueNode
{QueueDataType val;struct QueueNode* next;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;

(2)队列的初始化

//队列的初始化
void QueueInit(Queue* pq)
{assert(pq);pq->head = NULL;pq->tail = NULL;pq->size = 0;
}

(3)队列的销毁：先逐个销毁队列的节点，再销毁队列

//队列的销毁
void QueueDestory(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* Next = cur->next;free(cur);cur = Next;}pq->head = NULL;pq->tail = NULL;pq->size = 0;
}

(4)插入数据：为该数据开辟一个新节点，若原队列中有数据则让尾指针向后走一步，若无则头尾    指针均指向该新节点

//队尾入数据
void QueuePush(Queue* pq, QueueDataType x)
{//开辟一个新节点QNode* node = (QNode*)malloc(sizeof(QNode));if (node == NULL){perror("malloc fail");return;}node->val = x;node->next = NULL;//队列中没有节点if (pq->tail == NULL){pq->head = node;pq->tail = node;}else{pq->tail->next = node;pq->tail = node;}pq->size++;
}

(5)删除数据：删除头指针指向的节点，并让头指针向后走一步，若只有一个节点删除后需将尾指针置空

//队头出数据
void QueuePop(Queue* pq)
{assert(pq);assert(pq->size != 0);QNode* next = pq->head->next;free(pq->head);pq->head = next;if (pq->head == NULL){pq->tail = NULL;}pq->size--;
}

(6)获取队头元素

//获取队头数据
QueueDataType QueueFront(Queue* pq)
{assert(pq);return pq->head->val;
}

(7)获取队尾元素

//获取队尾数据
QueueDataType QueueBack(Queue* pq)
{assert(pq);return pq->tail->val;
}

(8)判断队列是否为空

//判断队列是否为空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}

(9)队列的大小

//获取队列有效数据个数
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}

三.栈与队列的相互转化

1.用栈实现队列

. - 力扣（LeetCode）

(1)思路：栈：先进后出，队列：先进先出

               创建两个栈实现队列中数据的删除

(2)解题方法：

1>自己实现栈

2>定义一个队列结构体包含两个栈

3>队列的创建：为队列结构体malloc一块空间，防止出函数时结构体被销毁

4>队列的销毁：先销毁两个栈，再销毁队列

5>队尾插数据：当两栈均为空栈时：随便在哪个空栈的栈顶插入数据均可

                          当有一个栈不为空时：在非空栈的栈顶插入数据

6>队头删数据：将非空栈的前size-1个数据导入空栈中，再删除队头的数据。此时对下次删除来说栈中数据顺序是错乱的，故还需要将原空栈的数据导回原非空栈中。

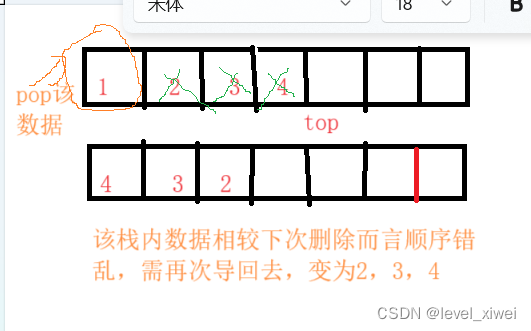
7>判断队列为空：当两个栈均为空时，队列为空

8>获取队尾数据：即非空栈的栈顶数据

(3)代码实现：

typedef int STDatatype;
typedef struct Stack
{STDatatype* arr;int top;//栈顶int capacity;//有效空间容量
}ST;//栈的初始化
void STInit(ST* ps);//栈的销毁
void STDestory(ST* ps);//入栈
void STPush(ST* ps, STDatatype x);//出栈
void STPop(ST* ps);//获取栈顶数据
STDatatype STTop(ST* ps);//判断栈是否为空
bool STEmpty(ST* ps);//栈的有效数据个数
int STSize(ST* ps);//栈的初始化
void STInit(ST* ps)
{assert(ps);ps->arr = NULL;//top指向栈顶后的一个元素,此时top等值于有效数据个数ps->top = 0;ps->capacity = 0;
}//栈的销毁
void STDestory(ST* ps)
{assert(ps);free(ps->arr);ps->arr = NULL;ps->capacity = ps->top = 0;
}//入栈
void STPush(ST* ps, STDatatype x)
{assert(ps);//判断是否需要增容if (ps->top == ps->capacity){int newcapacity = ps->capacity * 2==0 ? 4 : ps->capacity*2;STDatatype* tmp = (STDatatype*)realloc(ps->arr, sizeof(STDatatype) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}ps->arr = tmp;ps->capacity = newcapacity;}ps->arr[ps->top] = x;ps->top++;
}//出栈
void STPop(ST* ps)
{assert(ps);assert(ps->top > 0);ps->top--;
}//获取栈顶数据
STDatatype STTop(ST* ps)
{assert(ps);return ps->arr[ps->top-1];
}//判断栈是否为空
bool STEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}//栈的有效数据个数
int STSize(ST* ps)
{assert(ps);return ps->top;
}typedef struct {ST st1;ST st2;
} MyQueue;MyQueue* myQueueCreate() {MyQueue* pq=(MyQueue*)malloc(sizeof(MyQueue));STInit(&(pq->st1));STInit(&(pq->st2));return pq;
}void myQueuePush(MyQueue* obj, int x) {assert(obj);if(!STEmpty(&(obj->st1))){STPush(&(obj->st1),x);}else{STPush(&(obj->st2),x);}}int myQueuePop(MyQueue* obj) {assert(obj);ST* empty=&(obj->st1);ST* noempty=&(obj->st2);if(!STEmpty(&(obj->st1))){empty=&(obj->st2);noempty=&(obj->st1);}while(STSize(noempty)>1){STPush(empty,STTop(noempty));STPop(noempty);}STDatatype ret=STTop(noempty);STPop(noempty);//将noempty的数据导回empty,保证下次pop时数据顺序while(STSize(empty)>0){STPush(noempty,STTop(empty));STPop(empty);}return ret;
}int myQueuePeek(MyQueue* obj) {if(!STEmpty(&(obj->st1))){return obj->st1.arr[0];}else{return obj->st2.arr[0];}
}bool myQueueEmpty(MyQueue* obj) {return STEmpty(&(obj->st1)) && STEmpty(&(obj->st2));
}void myQueueFree(MyQueue* obj) {assert(obj);STDestory(&(obj->st1));STDestory(&(obj->st2));free(obj);obj=NULL;
}

2.用队列实现栈

. - 力扣（LeetCode）

(1)思路：栈：先进后出，队列：先进先出

               创建两个队列实现栈中数据的删除

(2)解题方法：

1>自己实现队列

2>定义一个栈结构体包含两个队列

3>栈的创建：为栈结构体malloc一块空间，防止出函数时结构体被销毁

4>栈的销毁：先销毁两个队列，再销毁栈

5>入栈：当两队列均为空队列时：随便在哪个空队列的队尾插入数据均可

                          当有一个队列不为空时：在非空队列的队尾插入数据

6>出栈：将非空队列的前size-1个数据导入空队列中，再删除栈顶元素。

7>判断栈为空：当两个队列均为空时，栈为空

8>获取栈顶数据：即非空队列的队尾元素

(3)代码实现：

typedef int QueueDataType;typedef struct QueueNode
{QueueDataType val;struct QueueNode* next;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;//队列的初始化
void QueueInit(Queue* pq);//队列的销毁
void QueueDestory(Queue* pq);//队尾入数据
void QueuePush(Queue* pq, QueueDataType x);//队头出数据
void QueuePop(Queue* pq);//获取队头数据
QueueDataType QueueFront(Queue* pq);//获取队尾数据
QueueDataType QueueBack(Queue* pq);//获取队列有效数据个数
int QueueSize(Queue* pq);//判断队列是否为空
bool QueueEmpty(Queue* pq);//队列的初始化
void QueueInit(Queue* pq)
{assert(pq);pq->head = NULL;pq->tail = NULL;pq->size = 0;
}//队列的销毁
void QueueDestory(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* Next = cur->next;free(cur);cur = Next;}pq->head = NULL;pq->tail = NULL;pq->size = 0;
}//队尾入数据
void QueuePush(Queue* pq, QueueDataType x)
{//开辟一个新节点QNode* node = (QNode*)malloc(sizeof(QNode));if (node == NULL){perror("malloc fail");return;}node->val = x;node->next = NULL;//队列中没有节点if (pq->tail == NULL){pq->head = node;pq->tail = node;}else{pq->tail->next = node;pq->tail = node;}pq->size++;
}//队头出数据
void QueuePop(Queue* pq)
{assert(pq);assert(pq->size != 0);QNode* next = pq->head->next;free(pq->head);pq->head = next;if (pq->head == NULL){pq->tail = NULL;}pq->size--;
}//获取队头数据
QueueDataType QueueFront(Queue* pq)
{assert(pq);return pq->head->val;
}//获取队尾数据
QueueDataType QueueBack(Queue* pq)
{assert(pq);return pq->tail->val;
}//获取队列有效数据个数
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}//判断队列是否为空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}typedef struct {Queue q1;Queue q2;
} MyStack;MyStack* myStackCreate() {MyStack* pst=(MyStack*)malloc(sizeof(MyStack));QueueInit(&(pst->q1));QueueInit(&(pst->q2));return pst;
}void myStackPush(MyStack* obj, int x) {if(!QueueEmpty(&(obj->q1))){QueuePush(&(obj->q1),x);}else{QueuePush(&(obj->q2),x);}
}int myStackPop(MyStack* obj) {Queue* empty=&(obj->q1);Queue* noempty=&(obj->q2);if(!QueueEmpty(&(obj->q1))){empty=&(obj->q2);noempty=&(obj->q1);}//把前size-1个数据移到空队列中while(QueueSize(noempty)>1){QueuePush(empty,QueueFront(noempty));QueuePop(noempty);}QueueDataType top=QueueFront(noempty);QueuePop(noempty);return top;
}int myStackTop(MyStack* obj) {if(!QueueEmpty(&(obj->q1))){return QueueBack(&(obj->q1));}else{return QueueBack(&(obj->q2));}
}bool myStackEmpty(MyStack* obj) {assert(obj);return QueueEmpty(&(obj->q1)) && QueueEmpty(&(obj->q2));
}void myStackFree(MyStack* obj) {assert(obj);QueueDestory(&(obj->q1));QueueDestory(&(obj->q2));free(obj);obj=NULL；
}

四.循环队列

. - 力扣（LeetCode）

1.定义：一种线性结构，基于先进先出原则，将队尾与队头连接起来构成循环

2.特点：有限空间，保证先进先出，从重复使用

3.思路：可以用数组实现，也可以用链表实现

用数组实现较为简单，用链表实现比较困难，下面小编将从两个角度来解释原因：

1>若使用单链表，在删除数据时不好获取待删除数据的前一个节点的位置，无法实现队尾的改变

2>若使用双向链表，占用内存太大，而且此时在判空判满时需要比较两个节点的地址比较麻烦

4.代码实现(以数组实现为例)：

(1)循环队列的结构体定义：数组指针，队头的下标，队尾下一个数据的下标，空间的大小

typedef struct {int* a;int head;//指向头int rear;//指向尾的下一个int k;//空间大小
} MyCircularQueue;

(2)循环队列的创建：

1>为循环队列malloc一块空间，防止出函数时，结构体被销毁

2>由于rear指向队尾的下一个数据，若直接开辟指定大小的空间，在插入最后一个数据时，rear会越界访问，此时我们称该情况为假溢出现象，为了解决假溢出我们可以采取以下两种措施

【1】为数组多开一块空间

【2】

MyCircularQueue* myCircularQueueCreate(int k) {MyCircularQueue* pc=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));//多开一块空间，解决假溢出问题pc->a=(int*)malloc(sizeof(int)*(k+1));pc->head=0;pc->rear=0;pc->k=k;return pc;
}

(3)循环队列的销毁：先销毁为数组开辟的空间，再销毁循环队列

void myCircularQueueFree(MyCircularQueue* obj) {free(obj->a);obj->a=NULL;free(obj);obj=NULL;
}

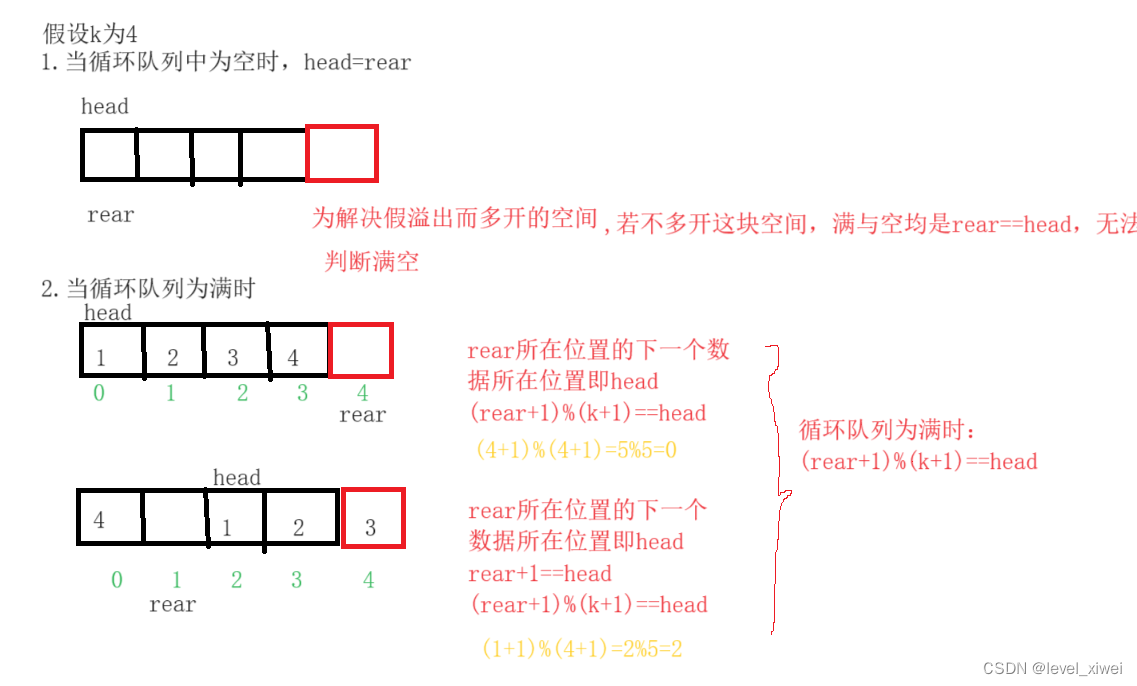
(4)循环队列的判空：

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {assert(obj);//头与尾的下一个指向同一位置即为空return obj->head==obj->rear;
}

(5)循环队列的判满：

bool myCircularQueueIsFull(MyCircularQueue* obj) {assert(obj);//尾的下一个和头指向的位置相同即为满return obj->head==(obj->rear+1)%(obj->k+1);
}

(6)循环队列插入数据：在队尾插入数据，让rear向后走一步，为了避免rear++后越界访问，需要将自增后的rear模上k+1，使其在有效下标内且可以完成循环

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {assert(obj);if(myCircularQueueIsFull(obj)){return false;}obj->a[obj->rear]=value;obj->rear++;obj->rear%=(obj->k+1);return true;
}

(7)循环队列删除数据：删除队头数据，让head向后走一步，为了避免head++后越界访问，需要将自增后的head模上k+1，使其在有效下标内且可以完成循环(原理同上，就不再赘述了)

ool myCircularQueueDeQueue(MyCircularQueue* obj) {assert(obj);if(myCircularQueueIsEmpty(obj)){return false;}obj->head++;obj->head%=(obj->k+1);return true;
}

(8)获取队尾元素：


int myCircularQueueRear(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj)){return -1;}else{return obj->rear==0?obj->a[obj->k]:obj->a[obj->rear-1];}
}

(9)获取队头元素：

int myCircularQueueFront(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj)){return -1;}else{return obj->a[obj->head];}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/704500.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

计算机网络 -- 序列化与反序列化

计算机网络 -- 序列化与反序列化

一 协议的重要性 我们都知道，在进行网络通信的过程中，通信的双方可以是不同的设备，不同的平台，不同的平台，比如说，手机用户和电脑用户进行通信，ios系统和安卓系统进行通信。 自己的数据&#xf…
阅读更多...
springMVC基础使用（示例）

springMVC基础使用（示例）

maven依赖&#xff08;javax.servlet-api版本与spring-webmvc班恩要匹配不然会报java.lang.NoSuchMethodError: javax.servlet.http.HttpServletRespons&#xff09;&#xff1a; <dependencies><dependency><groupId>javax.servlet</groupId><arti…
阅读更多...
【数组中重复的数据】leetcode,python

【数组中重复的数据】leetcode,python

和上题一样&#xff0c;【找到所有数组中消失的数字】 换个判断条件就行 class Solution:def findDuplicates(self, nums: List[int]) -> List[int]:nlen(nums)for i in nums:x(i-1)%nnums[x]n#只需要替换条件即可return [i1 for i,num in enumerate(nums) if num>(2*n)…
阅读更多...
办公园区建筑科技风效果(html+threejs)

办公园区建筑科技风效果(html+threejs)

办公楼科技风(Htmlthreejs) 初始化三维场景 function init() {container document.getElementById(container);camera new THREE.PerspectiveCamera(65, window.innerWidth / window.innerHeight, 0.1, 150000000);camera.position.set(550, 600, 690);scene new THREE.Sce…
阅读更多...
公域流量如何引流到私域流量？

公域流量如何引流到私域流量？

公域流量和私域流量是数字营销中常用的两种流量类型。公域流量指的是通过搜索引擎、社交媒体等公共平台获取的流量&#xff0c;而私域流量则是指企业自身拥有的用户群体和数据。那么&#xff0c;如何将公域流量引流到私域流量呢&#xff1f;下面我将为您详细解答。 1、提供有价…
阅读更多...
STM32--HC-SR501 热释电人体红外感应模块

STM32--HC-SR501 热释电人体红外感应模块

实物引脚图&#xff1a; 模块工作特性&#xff1a; 当人进入感应范围之后输出引脚输出高电平&#xff0c;人离开感应范围自动延时输出低电平 热释电效应&#xff1a; 热释电传感器&#xff0c;也称为人体红外传感器&#xff0c;其工作原理基于热释电效应。这种传感器由几个关…
阅读更多...
STM32 各外设GPIO配置

STM32 各外设GPIO配置

高级定时器TIM1/TIM8 通用定时器TIM2/3/4/5 USART SPI I2S I2C接口 BxCAN SDIO ADC/DAC 其它I/O功能
阅读更多...
层次式体系结构概述

层次式体系结构概述

1.软件体系结构 软件体系结构可定义为&#xff1a;软件体系结构为软件系统提供了结构、行为和属性的高级抽象&#xff0c;由构成系统的元素描述、这些元素的相互作用、指导元素集成的模式以及这些模式的约束组成。软件体系结构不仅指定了系统的组织结构和拓扑结构&#xff0c;并…
阅读更多...
Wiley数据库文献哪里比较全？去哪里下载比较高效

Wiley数据库文献哪里比较全？去哪里下载比较高效

Wiley出版社1807年创建于美国&#xff0c;是一家具有超过200年历史的全球知名的出版机构&#xff0c;面向专业人士、科研人员、教育工作者、学生、终身学习者提供必需的知识和服务。 Wiley及旗下的子品牌出版了超过500位诺贝尔奖得主的作品。Wiley Online Library为全学科期刊全…
阅读更多...
Jenkins 忘记登录密码怎么办

Jenkins 忘记登录密码怎么办

在安装Jenkins中遇到忘记登录密码该怎么呢&#xff1f;下面是一个解决办法 1. 先停止jenkins服务 我是用tomcat启动的jenkis 2. 找到config.yaml文件 find / -name config.xml命令执行后找到如下结果&#xff1a; /root/.jenkins/config.xml /root/.jenkins/users/admin_839…
阅读更多...
Java后端实现对象与文件接收数据（minio测试）

Java后端实现对象与文件接收数据（minio测试）

实现思路&#xff1a; 1. 两个接口实现&#xff0c;一个接对象数据(file)&#xff0c;一个接文件数据(json)。 2. json对象(base64String) 实体类信息 &#xff0c;请求体统一接收 3. file, String name ,String password ,String name &#xff0c; Controller层接收 统一…
阅读更多...
2023年国赛高教杯数学建模B题多波束测线问题解题全过程文档及程序

2023年国赛高教杯数学建模B题多波束测线问题解题全过程文档及程序

2023年国赛高教杯数学建模 B题 多波束测线问题 原题再现 单波束测深是利用声波在水中的传播特性来测量水体深度的技术。声波在均匀介质中作匀速直线传播&#xff0c;在不同界面上产生反射&#xff0c;利用这一原理&#xff0c;从测量船换能器垂直向海底发射声波信号&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023