题目描述
牛站
给定一张由 M M M 条边构成的无向图,点的编号为 1 ∼ 1000 1\sim 1000 1∼1000 之间的整数。
求从起点 S S S 到终点 E E E 恰好经过 K K K 条边(可以重复经过)的最短路。
注意: 数据保证一定有解。
输入格式
第 1 1 1 行:包含四个整数 K , M , S , E K,M,S,E K,M,S,E。
第 2.. M + 1 2..M+1 2..M+1 行:每行包含三个整数,描述一条边的边长以及构成边的两个点的编号。
输出格式
输出一个整数,表示最短路的长度。
样例 #1
样例输入 #1
2 6 6 4
11 4 6
4 4 8
8 4 9
6 6 8
2 6 9
3 8 9
样例输出 #1
10
提示
【数据范围】
2 ≤ M ≤ 100 2≤M≤100 2≤M≤100,
2 ≤ K ≤ 1 0 6 2≤K≤10^6 2≤K≤106
算法思想
倍增 + Floyd 求状态
根据题目描述,求从起点 S S S到终点 E E E恰好经过 K K K条边的最短路。考虑「Floyd」算法中的状态 d [ K , i , j ] d[K,i,j] d[K,i,j]表示经过编号 1 ∼ K 1\sim K 1∼K的点进行中转、从顶点 i i i到 j j j的最短距离。本题可以用类似的状态 d [ K , i , j ] d[K,i,j] d[K,i,j]表示为恰好经过 K K K条边,从顶点 i i i到 j j j的最短距离。
要计算状态 d [ K , i , j ] d[K,i,j] d[K,i,j],很容易想到 d [ K , i , j ] = m i n { d [ K − 1 , i , k ] + g [ k , j ] } d[K,i,j]=min\{d[K-1, i, k]+g[ k, j]\} d[K,i,j]=min{d[K−1,i,k]+g[k,j]},枚举一个中转点 k k k,从 K − 1 K-1 K−1阶段的状态转移到 K K K。这样做的时间复杂度为 K × n 3 K\times n^3 K×n3,从数据范围来看, 2 ≤ M ≤ 100 , 2 ≤ K ≤ 1 0 6 2≤M≤100,2≤K≤10^6 2≤M≤100,2≤K≤106,显然会TLE。
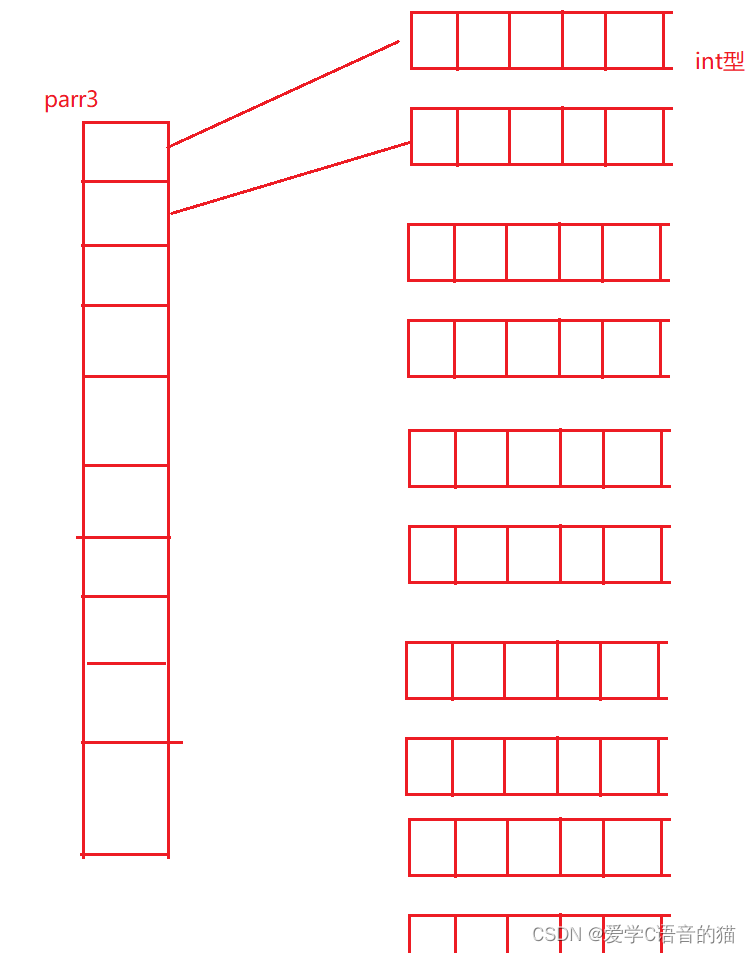
进一步分析,不妨假设 K = a + b K=a+b K=a+b,那么 d [ K , i , j ] = m i n { d [ a , i , k ] + d [ b , k , j ] } d[K,i,j]=min\{d[a,i,k]+d[b,k,j]\} d[K,i,j]=min{d[a,i,k]+d[b,k,j]},其中 k k k表示从 i i i出发经过恰好 a a a条边到达的顶点, 1 ≤ k ≤ n 1\le k\le n 1≤k≤n,如下图所示:
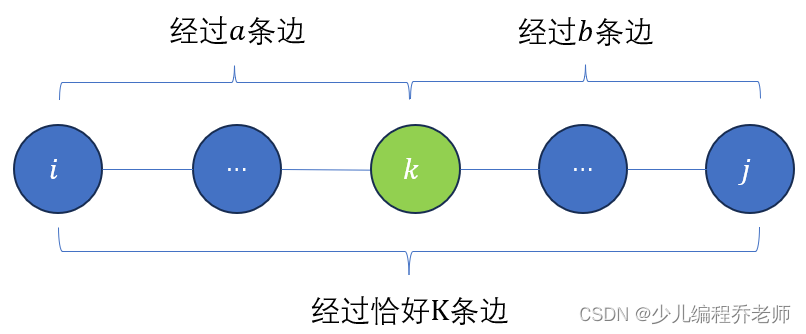
可以发现从顶点 i i i走到 k k k,和从顶点 k k k走到 j j j,这两个部分是完全独立的,并不相互依赖,所以先求前面、或者先求后面没有任何区别。也就是说,对于路径的组合可以是任意的,结合在一起答案不变,类似于加法结合律。
基于上述分析,可以使用快速幂“倍增”的思想,依次计算出 d [ 1 , i , j ] → d [ 2 , i , j ] → d [ 4 , i , j ] → . . . d[1,i,j]\to d[2,i,j]\to d[4,i,j]\to... d[1,i,j]→d[2,i,j]→d[4,i,j]→...,可以将时间复杂度优化为 O ( l o g K × n 3 ) O(logK\times n^3) O(logK×n3)。
离散化点集
除此之外,从给出的数据范围来看,边数 M ≤ 200 M\le200 M≤200, 200 200 200条边最多连接 400 400 400个点,那么就需要对所有点进行离散化,重新编号为 1 ∼ n 1\sim n 1∼n。
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 205;
int g[N][N], d[N][N];
int n, m, K, S, E;
map<int, int> idx; //离散化点集
void mul(int c[][N], int a[][N], int b[][N])
{static int temp[N][N];memset(temp, 0x3f, sizeof temp);for(int k = 1; k <= n; k ++)for(int i = 1; i <= n; i ++)for(int j = 1; j <= n; j ++)temp[i][j] = min(temp[i][j], a[i][k] + b[k][j]);memcpy(c, temp, sizeof temp);
}
void qmi()
{//初始话状态数组memset(d, 0x3f, sizeof d);for(int i = 1; i <= n; i ++) d[i][i] = 0;while(K){if(K & 1) mul(d, d, g); // d = d * gmul(g, g, g); //g = g * gK >>= 1;}
}
int main()
{cin >> K >> m >> S >> E;memset(g, 0x3f, sizeof g); //初始化邻接矩阵//离散化起点和终点,重新分配编号idx[S] = ++ n; idx[E] = ++ n; S = idx[S], E = idx[E];for(int i = 0; i < m; i ++){int a, b, c;cin >> c >> a >> b; //注意输入顺序//将点离散化,重新分配编号if(!idx.count(a)) idx[a] = ++ n;if(!idx.count(b)) idx[b] = ++ n;a = idx[a], b = idx[b]; g[a][b] = g[b][a] = min(g[a][b], c);}qmi(); //快速幂,倍增求状态cout << d[S][E] << endl;return 0;
}