【数据结构】C++语言实现二叉树的介绍及堆的实现(详细解读)

9efbcbc3d25747719da38c01b3fa9b4f.gif

 c语言中的小小白-CSDN博客c语言中的小小白关注算法,c++,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm=1001.2014.3001.5343

给大家分享一句我很喜欢我话：

知不足而奋进，望远山而前行！！！

铁铁们，成功的路上必然是孤独且艰难的，但是我们不可以放弃，远山就在前方，但我们能力仍然不足，所有我们更要奋进前行！！！

今天我们更新了二叉树内容，

🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝

树

首先我们为大家说一下树的概念和结构，树是一种非线性的数据结构，它是由n(n >= 0)个有限结点组成的一个具有层次关系的集合，把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

  • 有一个特殊的结点，称为根结点，根节点没有前驱结点。
  • 除跟根结点外，其余结点被分成M（M>0）个互不相交的集合T1、T2…Tm,其中每一个集合Ti(1<=i<=m)又是一棵结构与树类似的子树。每颗子树的根节点有且只有一个前驱，可以有0个或多个后继。
  • 因此，树是递归定义的。

有关树的一些概念：

  1. 节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的为6
  2. 叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I…等节点为叶节点非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G…等节点为分支节点
  3. 兄弟节点:具有相同父节点的节点互称为兄弟节点;如上图:B、C是兄弟节点
  4. 树的度:一棵树中，最大的节点的度称为树的度;如上图:树的度为6
  5. 节点的层次:从根开始定义起，根为第1层，根的子节点为第2层，以此类推;
  6. 树的高度或深度:树中节点的最大层次;如上图:树的高度为4（有两种说法-从0开始还是从1开始，空树-1，空树0）
  7. 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
  8. 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
  9. 森林:由m (m>0)棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是一个森林)——(日常很少碰到森林，并查集就是一个森林)

其中这些概念中第 4、6、7条较为重要，其余了解一下即可。

树的要求：

  • 子树是不相交的
  • 除了根结点之外，每个结点有且仅有一个父结点
  • 一个N个结点的树有N-1条边

树的表示

相对于线性表，树的结构就复杂很多了。最常用的表示方法——孩子兄弟表示法。

二叉树

与普通的树最大的不同是它最多只有两个子树。

特殊的二叉树

  1. 满二叉树：每一层都是满的。

    假设一棵满二叉树的高度是 h,那么它的总结点个数是：20+21+22+…2(h-1) =N。

    推导公式:2^h-1 = N;h = log2N+1以2位底N的对数+1。

  2. 完全二叉树

完全二叉树是个效率很高的数据结构，完全二叉树是由满二叉树引出来的。

假设树的高度是h,前h-1层是满的，最后一层不满，但是最后一层从左往右都是连续的。

最后一层最少有一个结点。

结点个数为:2^h-1-X= N,高度近似为:h = log2N+1+X以二为底N的对数+1

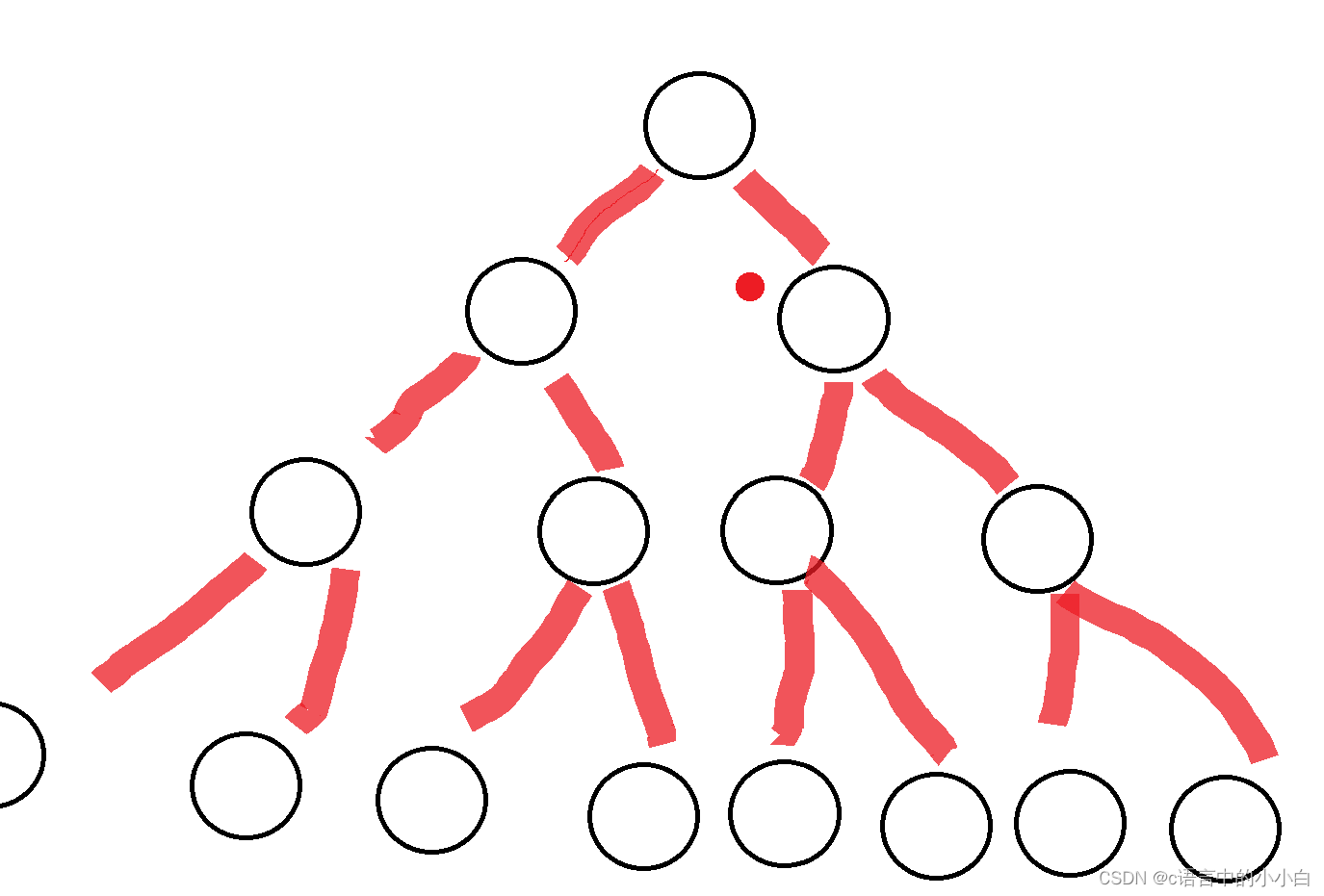
图有点难看不要介意

这些就是关于树的一些基本概念，下面我们来介绍一下关于树的实现。

堆的实现：

这里我们将会分为初始化、销毁、建堆、堆的删除、取出堆顶元素、判断是否为空、向上调整和向下调整这几步来完成。

头文件及堆结构的定义：

#pragma once
#include<stdio.h>
#include<iostream>
#include<stdlib.h>
#include<assert.h>
#include<algorithm>
#include<cmath>
#include<utility>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;

初始化：

//初始化
void HPInit(HP* php)
{assert(php);php->a = NULL;php->capacity = php->size= 0;}

销毁：

void HPDestroy(HP* php)
{assert(php);free(php);php->a = NULL;php->capacity = php->size = 0;}

向上调整：

//向上调整(小根堆)
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child>0){if (a[child] < a[parent])//小于就换就相当于建小堆//if (a[child] > a[parent])//大于就换就会变成大堆{std::swap(a[child], a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

建堆：

void HPPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc failed!!!");return;}php->a = tmp;php->capacity = newcapacity;}php->a[php->size++] = x;//向上调整AdjustUp(php->a, php->size - 1);
}

向下调整：

void AdjustDown(HPDataType* a, int n, int parent)
{//假设法//假设左孩子小int child = parent * 2 + 1;while(child<n){if (child + 1 < n &&a[child + 1] < a[child])//这里如果是左孩子大于右孩子，就要再加加child{++child;}if (a[child] < a[parent]){std::swap(a[child], a[parent]);parent = child;child = parent * 2 + 1;}else break;}}

删除堆顶的数据：

HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}

判空：

bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}

总代码：

TEST.c:

#include"Heap.h"void TestHeap1()
{int a[] = { 4,2,8,1,5,6,7,9 };HP hp;HPInit(&hp);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HPPush(&hp, a[i]);}while (!HPEmpty(&hp)){printf("%d ", HPTop(&hp));HPPop(&hp);}HPDestroy(&hp);
}void HeapSort(int* a, int n)
{//首先建堆//升序：建大堆//降序：建小堆for (int i=0;i<n;i++){AdjustUp(a, i);}int end = n - 1;///这里>0即可，因为=0时只剩下最后一个，就不再需要继续进行了while (end>0)//思路就是：比如我们升序排序，那么我们就利用大根堆，每次都将最大的那个数放在最顶上，然后将它和最后一个交换，然后让整体的大小--，那么最后一个就不再会受影响{std::swap(a[0], a[end]);AdjustDown(a, end, 0);--end;}}void TestHeap2()
{int a[] = { 4,2,8,1,5,6,9,7,3,10,23,14,125 };HeapSort(a, sizeof(a) / sizeof(0));for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++){std::cout << a[i] << " ";}
}int main()
{TestHeap2();return 0;
}

Heap.c:

#include"Heap.h"//初始化
void HPInit(HP* php)
{assert(php);php->a = NULL;php->capacity = php->size= 0;}//销毁
void HPDestroy(HP* php)
{assert(php);free(php);php->a = NULL;php->capacity = php->size = 0;}//向上调整(小根堆)
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child>0){if (a[child] < a[parent])//小于就换就相当于建小堆//if (a[child] > a[parent])//大于就换就会变成大堆{std::swap(a[child], a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//建堆
void HPPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc failed!!!");return;}php->a = tmp;php->capacity = newcapacity;}php->a[php->size++] = x;//向上调整AdjustUp(php->a, php->size - 1);
}//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{//假设法//假设左孩子小int child = parent * 2 + 1;while(child<n){if (child + 1 < n &&a[child + 1] < a[child])//这里如果是左孩子大于右孩子，就要再加加child{++child;}if (a[child] < a[parent]){std::swap(a[child], a[parent]);parent = child;child = parent * 2 + 1;}else break;}}//删除堆顶的数据
void HPPop(HP* php)
{assert(php);assert(php->size > 0);std::swap(php->a[0], php->a[php->size - 1]);//就是将第一个与最后一个换掉，然后将他们向下调整，php->size--;//直接size--删去最后一个元素AdjustDown(php->a, php->size, 0);
}//取出堆顶数据
HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}

Heap.h:

#pragma once
#include<stdio.h>
#include<iostream>
#include<stdlib.h>
#include<assert.h>
#include<algorithm>
#include<cmath>
#include<utility>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;//初始化
void HPInit(HP* php);//销毁
void HPDestroy(HP* php);//建堆
void HPPush(HP* php,HPDataType x);//堆的删除
void HPPop(HP* php);//取出堆顶数据
HPDataType HPTop(HP* php);bool HPEmpty(HP* php);void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int n, int parent);

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/704877.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

vue3专栏项目 -- 六、上传组件（上）

vue3专栏项目 -- 六、上传组件（上）

1、上传组件需求分析 我们还需要新建和展示文章&#xff0c;新建文章自然是发送post请求&#xff0c;同时在post中自带对应的数据&#xff0c;展示文章就是根据id取出已有的数据并且展示出来。 这里有一个难点就是上传组件&#xff0c;上传文件是App应用中最基本的需求&#…
阅读更多...
白话Wide Deep_推荐系统经典论文

白话Wide Deep_推荐系统经典论文

文章目录 1.1 简介1.2 基本概念1.2.1 线性特征和非线性特征1.2.2 稀疏向量和稠密向量1.2.3 模型的记忆能力和泛化能力 1.3 提出Wide & Deep模型的背景1.4 Wide & Deep模型结构1.4.1 Wide模块1.4.2 Deep模块1.4.3 Wide & Deep 联合&#xff08;joint&#xff09;训练…
阅读更多...
【SpringBoot】SpringBoot整合jasypt进行重要数据加密

【SpringBoot】SpringBoot整合jasypt进行重要数据加密

&#x1f4dd;个人主页&#xff1a;哈__ 期待您的关注 目录 &#x1f4d5;jasypt简介 &#x1f525;SpringBoot使用jasypt &#x1f4c2;创建我需要的数据库文件 &#x1f4d5;引入依赖 &#x1f513;配置数据库文件&#xff08;先不进行加密&#xff09; &#x1f319;创…
阅读更多...
【SQL】SQL常见面试题总结（2）

【SQL】SQL常见面试题总结（2）

目录 1、增删改操作1.1、插入记录&#xff08;一&#xff09;1.2、插入记录&#xff08;二&#xff09;1.3、插入记录&#xff08;三&#xff09;1.4、更新记录&#xff08;一&#xff09;1.5、更新记录&#xff08;二&#xff09;1.6、删除记录&#xff08;一&#xff09;1.7、…
阅读更多...
20240511每日运维----聊聊nignx改配置所有的nginx改完unknow

20240511每日运维----聊聊nignx改配置所有的nginx改完unknow

1、改配置所有的nginx改完unknow src/core/nginx.h src/http/ngx_http_header_filter_module.c src/http/ngx_http_special_response.c src/http/v2/ngx_http_v2_filter_module.c 2、make 3、去objs里面把nginx文件替换过去sbin/nginx
阅读更多...
254 基于matlab的钢筋混凝土非线性分析

254 基于matlab的钢筋混凝土非线性分析

基于matlab的钢筋混凝土非线性分析&#xff0c;根据梁本构关系&#xff0c;然后进行非线性分析&#xff0c;绘制弯矩-曲率曲线。可设置梁的截面尺寸、混凝土本构&#xff0c;钢筋截面面积等相关参数&#xff0c;程序已调通&#xff0c;可直接运行。 254 钢筋混凝土非线性分析 弯…
阅读更多...
五丰黎红引领新营销模式：布局一物一码数字化营销，提高调味品销量和复购率

五丰黎红引领新营销模式：布局一物一码数字化营销，提高调味品销量和复购率

调味品行业的销售渠道主要有餐饮、家庭消费和食品加工&#xff0c;按销售额的占比约为6&#xff1a;3&#xff1a;1&#xff0c;餐饮行业是调味品行业的供需主力。在餐饮行业中&#xff0c;“大厨”这一角色具有十分重要的地位。因此&#xff0c;借助大厨的力量成为了许多调味品…
阅读更多...
基于SpringBoot的竹宣非遗宣传网站

基于SpringBoot的竹宣非遗宣传网站

摘要 随着互联网的普及和数字化时代的到来&#xff0c;竹编等非物质文化遗产的保护与传承面临新的机遇和挑战。该研究旨在使用SpringBoot后端框架与Vue前端框架&#xff0c;构建一个竹编非遗宣传网站&#xff0c;通过丰富的展示形式和交互体验&#xff0c;提升公众对竹编这一非…
阅读更多...
不用投稿邮箱，怎样向各大新闻媒体投稿？

不用投稿邮箱，怎样向各大新闻媒体投稿？

身为单位的信息宣传员,我深知肩上责任重大。每个月,完成单位在媒体上投稿发表文章的考核任务,就如同一场无声的赛跑,既要保证速度,更要注重质量。起初,我遵循“前辈们”的老路,一头扎进了邮箱投稿的海洋。但很快,现实给了我一记重拳——邮箱投稿的竞争犹如千军万马过独木桥,稿件…
阅读更多...
树链剖分详解，看这一篇就够了

树链剖分详解，看这一篇就够了

前置知识&#xff1a; 树形结构链式前向星(熟练)线段树(熟练)DFS序(熟练)LCA(了解定义) 什么是树链剖分 树链剖分其实有两种&#xff1a;重链剖分和长链剖分。重链剖分就是把儿子节点最重的儿子称为重儿子&#xff0c;把树分成若干条重链&#xff08;如图一&#xff09;&#…
阅读更多...
【Linux】系统登录，调用shell，shell配置文件，shell命令，特殊符号，shell快捷键，Linux运行级别，解决无限登录问题，修改提示符

【Linux】系统登录，调用shell，shell配置文件，shell命令，特殊符号，shell快捷键，Linux运行级别，解决无限登录问题，修改提示符

目录 Linux系统的登录方式 以及 调用shell Linux shell 以及 shell配置文件 shell 命令 shell 特殊符号 shell 快捷键 Linux操作系统运行级别 单用户模式下解决无限登录问题 centos7修改命令行提示符 PS1 补充、centos7没有滚动条 Linux系统的登录方式 以及 调用shell…
阅读更多...
蓝桥杯-外卖店优先级(简单写法)

蓝桥杯-外卖店优先级(简单写法)

“饱了么”外卖系统中维护着 N 家外卖店&#xff0c;编号 1∼N。 每家外卖店都有一个优先级&#xff0c;初始时 (0 时刻) 优先级都为 0。 每经过 1 个时间单位&#xff0c;如果外卖店没有订单&#xff0c;则优先级会减少 1&#xff0c;最低减到 0&#xff1b;而如果外卖店有订…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023