前言

简单介绍一下我自己：博主专注建模四年，参与过大大小小数十来次数学建模，理解各类模型原理以及每种模型的建模流程和各类题目分析方法。参与过十余次数学建模大赛，三次美赛获得过二次M奖一次H奖，国赛二等奖。**提供免费的思路和部分源码，以后的数模比赛只要我还有时间肯定会第一时间写出免费开源思路。**博主紧跟各类数模比赛，每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码且完全免费。希望有需求的小伙伴不要错过笔者精心打造的文章。

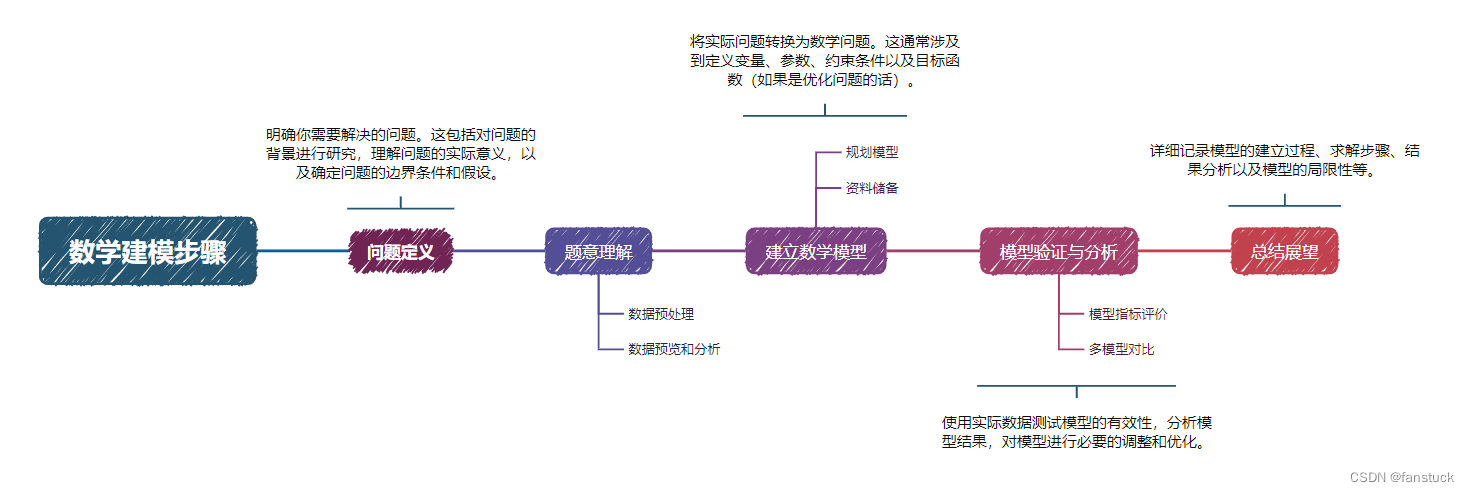
数学建模的基本步骤大致如下：

1. 问题定义：明确你需要解决的问题。这包括对问题的背景进行研究，理解问题的实际意义，以及确定问题的边界条件和假设。
2. 建立数学模型：将实际问题转换为数学问题。这通常涉及到定义变量、参数、约束条件以及目标函数（如果是优化问题的话）。
3. 求解数学模型：选择合适的数学工具和方法求解模型。这可能包括解析方法、数值方法、仿真等。
4. 模型验证与分析：使用实际数据测试模型的有效性，分析模型结果，对模型进行必要的调整和优化。
5. 撰写模型报告：详细记录模型的建立过程、求解步骤、结果分析以及模型的局限性等。
   

问题 2

我们在第一问的基础之上我们进行了对空缺值填充并且二表进行了拼接，从而得到了文物风化状态成分表以及无风化状态的两张表格：

文物风化状态成分表：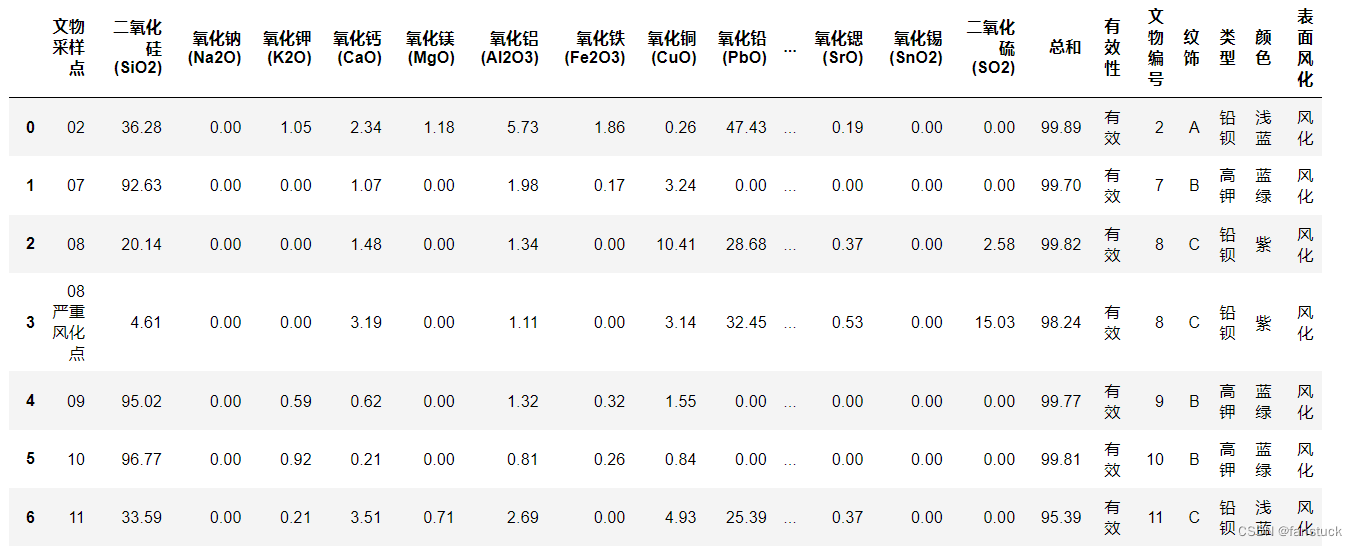
文物无风化状态成分表：
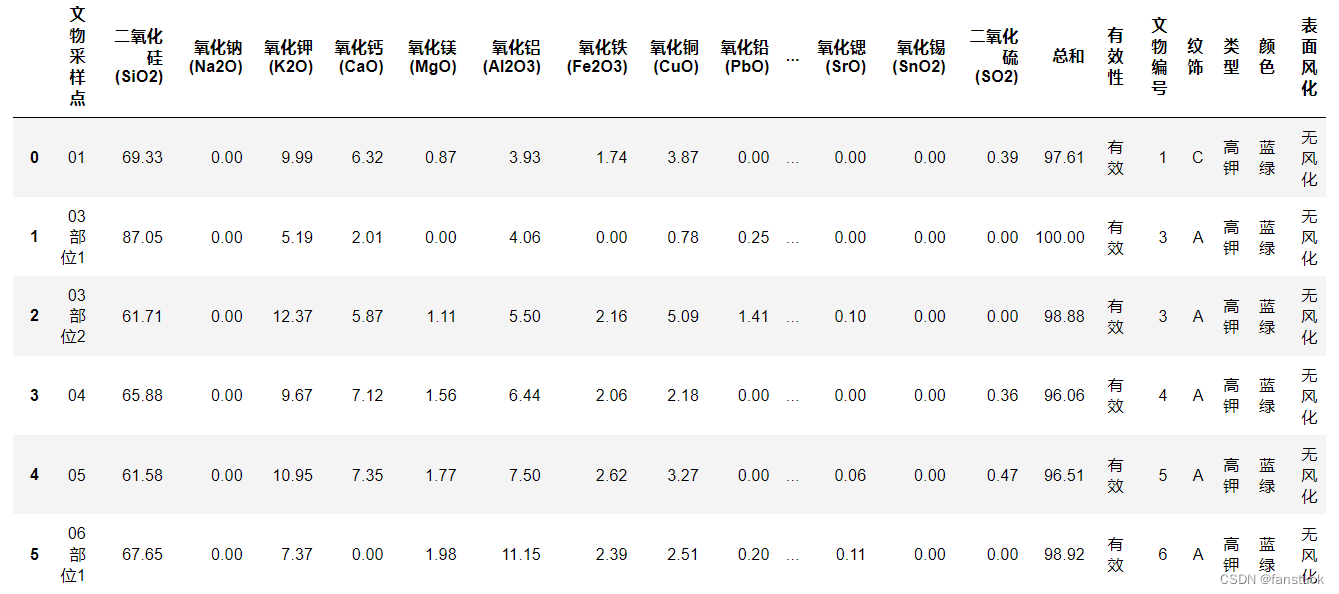我们根据问题2的要求来提取数据：依据附件数据分析高钾玻璃、铅钡玻璃的分类规律，现将风化的这二者玻璃的数据都提取出来：
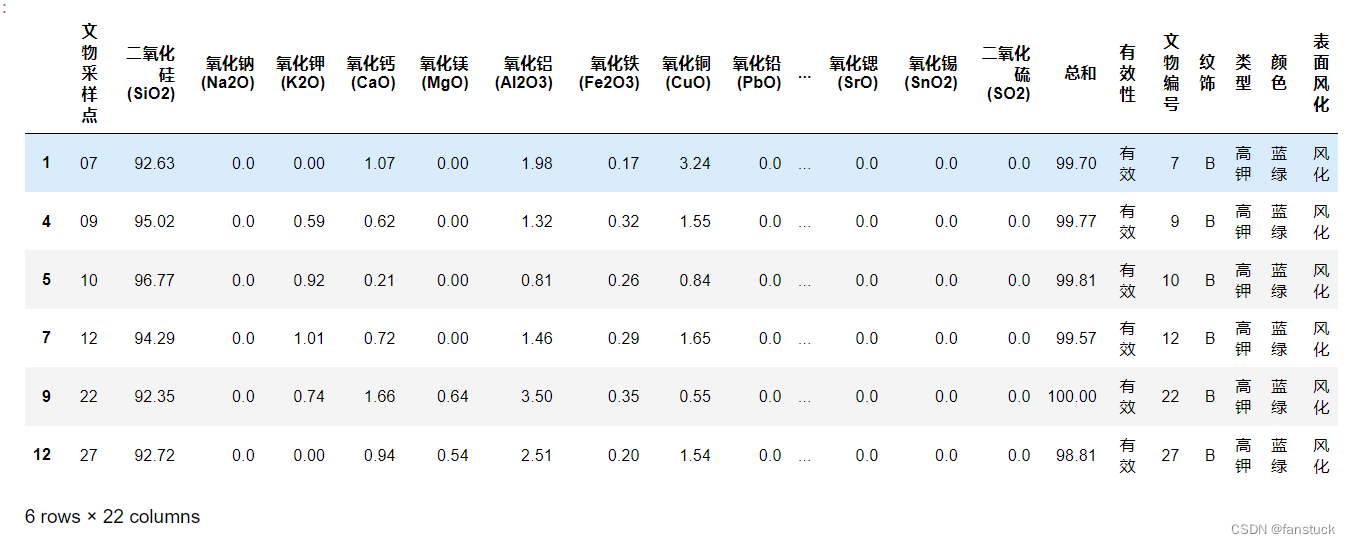这里选择的是高钾的玻璃数据，由于亚类数目和标签我们是不知道的，固我们选择无标签算法，也就是聚类算法，很自然的采用K-mean算法.

K-mean聚类建模

K-means算法实现

我们知道我们是使用聚类算法的目的就是从大量数据中将他们具有相关性的特征输入，然后通过算法返回标签类型。也就是说该算法的目的就是将具有相同特性的数据归纳为一类。当然我们的算法是贪心的，尽可能将所有相同类型的数据归为一类，本质还在站在分类的角度上，只不过没有标签需要我们进行运算得出。

那么既然是找到具有相同性质的数据，那么回到原始的方法，例如KNN算法，我们只需要去根据两个数据点的距离去判断他们是否属于一类，其实聚类的思想也类似，只不过我们选择圆心的点不再是判断数据类型的点，而是划分为一类标签的最大范围半径的点，类似画一个最大的圆：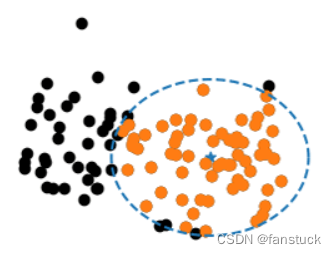

step1:选取K值

k 的选择一般是按照实际需求进行决定，或在实现算法时直接给定 k 值。这是基于项目你想要聚类的个数来决定的，但是也有不确定的情况，我们可能需要去一个最优的K值来将数据很好的归类达到最大化区分类别，这时候就需要思考从数据角度出发，应该进行怎么样的计算能够得到最优的K。

# 检查数据点的数量
n_samples = data.shape[0]# 计算并存储轮廓系数
scores = []  # 存放轮廓系数
for i in range(2, min(10, n_samples)):  # 确保i不超过n_samplesKmeans_model = KMeans(n_clusters=i)predict_ = Kmeans_model.fit_predict(data)score = silhouette_score(data, predict_)scores.append(score)print(f"Number of clusters: {i}, Silhouette Score: {score}")# 绘制轮廓系数图
plt.plot(range(2, min(10, n_samples)), scores, marker='x')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.title('Silhouette Scores vs Number of Clusters')
plt.show()

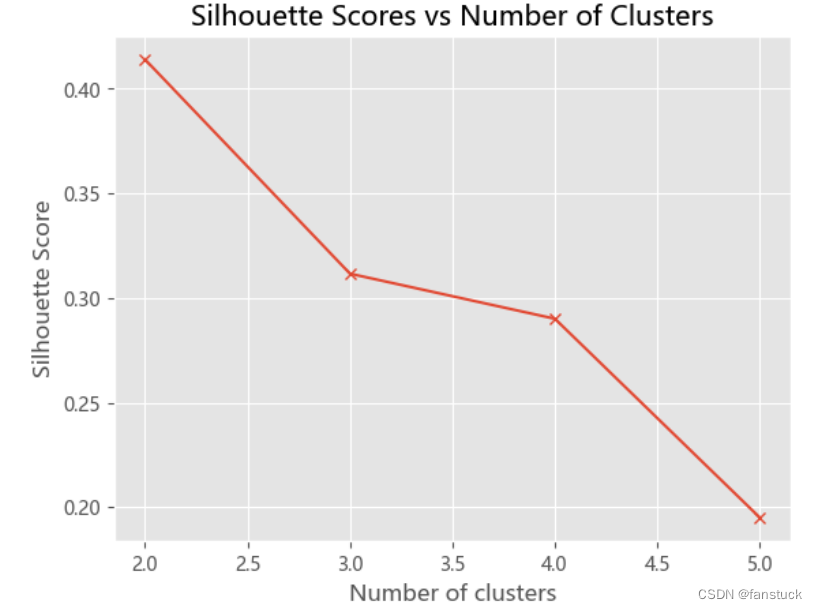
在回归分析中通常用SSE表示，其大小用来表明函数拟合的好坏。将残差平方和除以自由度n-p-1(其中p为自变量个数)可以作为误差方差σ2的无偏估计，通常用来检验拟合的模型是否显著也用来寻找K值。

主要思想：当k小于真实聚类数时，随着k的增大，会大幅提高类间聚合程度，SSE会大幅下降，当k达到真实聚类数时，随着k的增加，类间的聚合程度不会大幅提高，SSE的下降幅度也不会很大，所以k/SSE的折线图看起来像一个手肘，我们选取肘部的k值进行运算。

也就是聚为三类。

step2:计算初始化K点

初始质心随机选择即可，每一个质心为一个类。对剩余的每个样本点，计算它们到各个质心的欧式距离，并将其归入到相互间距离最小的质心所在的簇。

def euclDistance(x1, x2):return np.sqrt(sum((x2 - x1) ** 2))
def initCentroids(data, k):numSamples, dim = data.shape# k个质心，列数跟样本的列数一样centroids = np.zeros((k, dim))# 随机选出k个质心for i in range(k):# 随机选取一个样本的索引index = int(np.random.uniform(0, numSamples))# 作为初始化的质心centroids[i, :] = data[index, :]return centroids

step3:迭代计算重新划分

• 计算各个新簇的质心。
• 在所有样本点都划分完毕后，根据划分情况重新计算各个簇的质心所在位置，然后迭代计算各个样本点到各簇质心的距离，对所有样本点重新进行划分
• 重复2. 和 3.，直到质心不在发生变化时或者到达最大迭代次数时

# 传入数据集和k值
def kmeans(data, k):# 计算样本个数numSamples = data.shape[0]# 样本的属性，第一列保存该样本属于哪个簇，第二列保存该样本跟它所属簇的误差clusterData = np.array(np.zeros((numSamples, 2)))# 决定质心是否要改变的质量clusterChanged = True# 初始化质心centroids = initCentroids(data, k)while clusterChanged:clusterChanged = False# 循环每一个样本for i in range(numSamples):# 最小距离minDist = 100000.0# 定义样本所属的簇minIndex = 0# 循环计算每一个质心与该样本的距离for j in range(k):# 循环每一个质心和样本，计算距离distance = euclDistance(centroids[j, :], data[i, :])# 如果计算的距离小于最小距离，则更新最小距离if distance < minDist:minDist = distance# 更新最小距离clusterData[i, 1] = minDist# 更新样本所属的簇minIndex = j# 如果样本的所属的簇发生了变化if clusterData[i, 0] != minIndex:# 质心要重新计算clusterChanged = True# 更新样本的簇clusterData[i, 0] = minIndex# 更新质心for j in range(k):# 获取第j个簇所有的样本所在的索引cluster_index = np.nonzero(clusterData[:, 0] == j)# 第j个簇所有的样本点pointsInCluster = data[cluster_index]# 计算质心centroids[j, :] = np.mean(pointsInCluster, axis=0)return centroids, clusterData

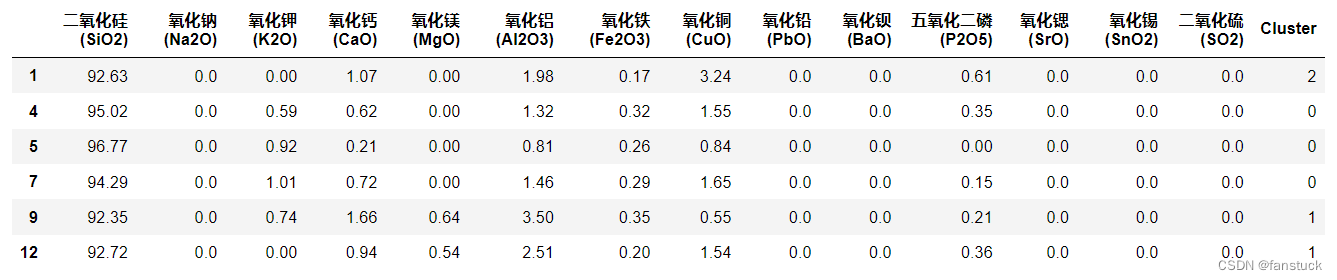
这样就聚类完成了，同理其他铅钡玻璃和未风化的那组也是一样进行聚类分类，按照上述流程再同步模型计算一遍便可以完成第二问了。

希望大家支持一下！到这里第一问建模就结束了，想要了解更多的欢迎联系博主再向大家推荐一下笔者精心打造的专栏。此专栏的目的就是为了让零基础快速使用各类数学模型以及代码，每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛，每场数模竞赛博主都会将最新的思路：