最短路径

拓扑序

有这样一个问题：

我们给定一张 \(n\) 个点 \(m\) 条边的有向无环图（DAG），请求出从 \(1\) 号结点出发，到达任意结点的最短路径，保证 \(s\) 可以到达任意结点，\(n,m\leq 10^7\)。

我们以下面这张图为例。

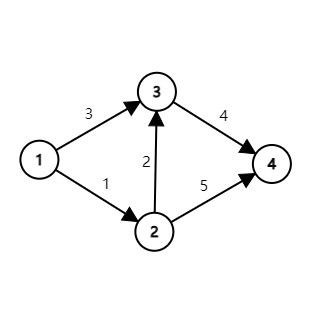
如果我们想求 \(1 \rightarrow 4\) 的路径， 我们不难发现，找到 \(1 \rightarrow 4\) 的最短路径，就需要先找到 \(1 \rightarrow 2\) 或 \(1\rightarrow 3\) 的最短路径，\(1 \rightarrow 2\) 的路径只有一条，而 \(1\rightarrow 3\) 的最短路径则是 \(\min(1\rightarrow 3,1\rightarrow 2+2\rightarrow 3)\)，而求出这里的最短路径，我们还需要需要先找到 \(1\rightarrow 1\) 的最短路径，\(1\rightarrow 1\) 的最短路径很明显是 \(0\)，这样便可以求出 \(1\) 到任意结点的最短路径了。

我们发现，上图我们按照 \(1,2,3,4\) 的顺序遍历，这种顺序是拓扑序，我们只要按照拓扑序依次求解最短路，在拓扑排序过程中，删除出边指向的结点入度时，顺带更新出边指向结点的最短路，这样便可以求得答案了。

\(\texttt{code}\)

//dist[i] 1 到 i 的最短路径长度
//deg[i] i 的入度
void topu(int s){for(int i=1;i<=n;i++){dist[i]=-1e9;//边权可能为负数}q.push(s);dist[s]=0;while(!q.empty()){int k=q.front();q.pop();for(auto x:g[k]){dist[x.first]=min(dist[x.first],dist[k]+x.second);//更新最短路deg[x.first]--;if(deg[x.first]==0){//拓扑排序入队q.push(x.first);}}}
}

该解法的时间复杂度是 \(O(n+m)\)。

Floyd

上面我们讨论了从某一固定结点出发到达其他任何一个其他结点的最短路径，这种问题被称为单源最短路问题，有时候我们也会关心从任意结点，到任意结点的最短路径，这样的问题被称为全源最短路问题。

我们有一个简单的算法可以解决这样的问题。Floyd 算法的思路是，我们每次枚举一个中间结点，利用这个中间结点更新任意两点之间的最短路。 由于是求任意两点的最短路，所以我们经常采用邻接矩阵模型解决这个问题。

\(\texttt{code}\)

int g[MAXN][MAXN],dist[MAXN][MAXN];
void floyd(){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dist[i][j]=g[i][j];}}for(int i=1;i<=n;i++){dist[i][i]=0;}for(int k=1;k<=n;k++){//枚举中间点for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){//枚举任意两点dist[i][j]=min(dist[i][j],dist[i][k] + dist[k][j]);//不经过 k 和经过 k 的路径求最小}}}
}

该解法的时间复杂度是 \(O(n^3)\)。

以最上面那张图为例，当我们枚举 \(k=1\) 时，我们考虑了所有途径 \(1\) 号结点，并且边数为 \(2\) 的最短路径。此时，最短路被更新为由一条路径或者两条边（必须经过 \(1\) 号结点）构成的最短路。

接着我们再枚举 \(k=2\)，我们考虑了所有途径 \(2\) 号结点，边数为 \(2\) 或者 \(3\) 的最短路径。现在，我们的最短路被更新为由 \(1\)条，\(2\) 条或者 \(3\) 条边构成的，中间可能途径 \(1\) 或者 \(2\) 号结点的最短路。

我们不难发现，只需要按照上述规则归纳下去，经过 \(n\) 次枚举，我们得到的应该是经过 \(1\)条，\(2\) 条，......，\(n\) 条边构成的，中间可能途径 \(1,2,3,......n\) 的最短路。这不就是所有可能的情况对应的最短路径吗？

Dijkstra

Dijkstra 算法解决的是单源最短路的且边权全为正的问题，它的思想大致是：每次选择一个最短路径长度已经确定的结点，然后通过从这个结点出发的边，更新其余还未完全确定最短路径长度的结点。这样反复确定 \(n\) 次，就确定了所有结点的最短路。

因为边权为正数，所以当前未考虑的距离最小的结点一定不会被当前未考虑的距离较大的结点再额外加一条边给更新，所以从贪心的角度来说，当前未考虑的距离最小的 结点其最短路径长度已经确定下来了。

\(\texttt{code}\)

int g[MAXN][MAXN],dist[MAXN],vis[MAXN];//vis[i] 标记是否已选过
int dijkstra(int s){memset(dist,0x3f,sizeof(dist));dist[s]=0;for(int i=1;i<n;i++){int minn=-1,pos=2e9;for(int j=1;j<=n;j++){if(!vis[j]&&dist[j]<pos){//选择最短路径最小的未选过的结点minn=j;pos=dist[j];}}if(minn==-1){//图不连通break;}vis[minn]=1;for(int j=1;j<=n;j++){dist[j]=min(dist[j],dist[minn]+g[minn][j]);//从选中的已确定最短路的结点额外走一步}}
}

该解法的时间复杂度为 \(O(n^2)\)，适用于稠密图。

当图为稀疏图时，我们可以使用堆对 Dijkstra 算法进行优化。

上面的解法中我们用循环找出最短路径长度最小的结点，我们可以采用一个堆，维护一个二元组，包含结点编号 \(u\)，以及源点到 \(u\) 的最短路径长度。每次通过一条边更新 \(u\) 的最短路径的时候，我就把新的最短路径加入到堆里面。这样我就能保证堆顶的是当前最短路径长度最小的结点。

\(\texttt{code}\)

vector<pair<int,int>> g[MAXN];
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;
int dis[MAXN],vis[MAXN];
int dijkstra(int s){memset(dis,0x3f,sizeof(dis));dis[s]=0;pq.push(make_pair(0,s));//把初始结点加入堆中while(!pq.empty()){pair<int,int> k=pq.top();pq.pop();if(vis[k.second]) continue; //每个结点只取出一次，如果取出多次，则不是最短路vis[k.second]=1;for(int i=0;i<g[k.second].size();i++){int to=g[k.second][i].first;int w=g[k.second][i].second;if(dis[to]>k.first + w){dis[to]=k.first + w;pq.push(make_pair(dis[to],to)); //把更新的最短路加入堆中}}}if(dis[n]==0x3f3f3f3f) return -1;else return dis[n];
}

该解法的时间复杂度是 \(O(m \log m)\)，适用于稀疏图，但在稠密图时还不如普通的 Dijkstra。

Bellman-ford

Bellman-ford 算法适合在图存在负权边的时候求解单源最短路。这是因为，当我们运行 Dijkstra的时候，我们依赖一个性质，就是当前未确定最短路的结点之中，最短路长度最小的结点它的最短路实际已经确定下来了。反过来想，如果我们未确定该结点的最短路，那么到其他结点的最短路都比到该结点的最短路长，加上一条正权边之后，路径长度只会更长，所以最短路长度最小的结点，它的最短路已经确定下来了。

但是如果有负权边，那就不一定了，我们不能保证当前未确定最短路的结点之中最短路长度最小的结点的最短路已经确定下来了，因为我们可能先移动到一个最短路比它长的结点，然后通过经过一条负权边的方法使得答案变得更小。

而 Bellman-ford 算法的思想大致是如果图里存在一条最短路，那么最短路的长度不会超过 \(n-1\)。所以我枚举 \(n-1\) 轮，每一轮枚举所有的边，通过枚举出来的边， 把源点出发到其他结点的最短路逐渐构建出来。

\(\texttt{code}\)

struct edge{int from,to,w;
}edges[MAXM];//存边
int dist[MAXN];
void Bellman_Ford(int s){memset(dist,127/3,sizeof(dist));dist[s]=0;for(int i=1;i<n;i++){for(int j=1;j<=m;j++){if(dist[edges[j].from]+edges[j].w<dist[edges[j].to]){dist[edges[j].to] = dist[edges[j].from] + edges[j].w;}}}
}

该解法的时间复杂度是 \(O(nm)\)，但在稠密图是会退化到 $O(n^3) $，所以在只有正权边的情况下，不如 Dijkstra。

使用队列优化 Bellman-ford（SPFA）

\(\texttt{code}\)

vector<pair<int,int>> g[MAXN]; //邻接表模型
queue<int> q;//采用队列优化，只保存结点编号，不保存路径长度
int dis[MAXN],vis[MAXN];
int PushTime[MAXN]; //记录进队此时，如果这个次数达到n次，说明有负环
int n,m;
void QBellman_Ford(int s){memset(dis,0x3f,sizeof(dis));dis[s]=0;q.push(s);//把初始结点加入队列中PushTime[s]++;while(!q.empty()){int k=q.front();q.pop();vis[k]=0;//标记它又可以放回队列了for(int i=0;i<g[k].size();i++){int to = g[k][i].first;int w = g[k][i].second;if(dis[to] > dis[k] + w){dis[to] = dis[k] + w;if(!vis[to]){PushTime[to]++;q.push(to); //把更新的最短路加入队列中vis[to] = 1;}}}}if(dis[n]==0x3f3f3f3f)cout<<"impossible";else cout<<dis[n];
}

注意，该解法最坏情况下时间复杂度还是 \(O(nm)\)。