CF-945(已更A,B)

CF-945（A，B）

A

分析

模拟

合法情况下三个数的和只能是偶数：题中的两种操作显然都不会改变和的奇偶性

这点我的代码中没有用到

要使平局数最多，一定是最大的两个数减一，重复这个过程，直到两个较小的数都为零，且最大数一定是偶数，否则不合法：可以由题意和样例想到

代码

int a[4]; 
void solve(){cin>>a[0]>>a[1]>>a[2];int f=0,ans=0;while(1){sort(a,a+3);				if(a[1]==0&&a[2]&1){f=1;break;}if(a[0]==a[1]&&a[0]==0){break;}		a[1]--,a[2]--;ans++;}if(f){cout<<"-1\n";return;}cout<<ans<<endl;
}
 

B

二分答案、包含种类信息（此题是二进制下的位数）的前缀和

分析

二分可行的单调性在于k越大，长度为k的区间或和一定是非递减的，同时n个数的或和sum一定要是等于所有长度为k的区间或和的，所以我们可以二分k，每次二分去判断长度为k的区间或和是否等于sum

技巧-区间或和

其实是拆位算贡献

p[i][j]表示前i个数字中二进制下第j位为1的数量

rep(j,0,21) p[i][j]=p[i-1][j];
rep(j,0,21){if(a[i]>>j&1){p[i][j]++;}
}

对样例打表：

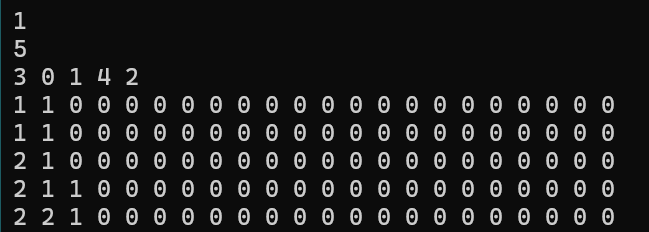
对于二进制下每一位只要有1就对区间或和有贡献，所以可以由此得到区间或和

int res=0;
rep(j,0,21){//区间[i,i+k-1]的或和if(p[i+k-1][j]-p[i-1][j]){res+=1ll<<j;}
}

代码

const int N=2e5+3;
int a[N],p[N][22],n,sum;
bool ck(int k){rep(i,1,n-k+1){int res=0;rep(j,0,21){if(p[i+k-1][j]-p[i-1][j]){res+=1ll<<j;}}if(res<sum){return true;}}return false;
} 
void solve(){cin>>n;sum=0;rep(i,1,n){cin>>a[i];rep(j,0,21) p[i][j]=p[i-1][j];per(j,21,0){if(a[i]>>j&1){p[i][j]++;}}sum|=a[i];}if(n==1){cout<<"1\n";return;}int l=0,r=n,mid;while(r-l>1){mid=l+r>>1;if(ck(mid)) l=mid;else r=mid; //cout<<l<<" "<<r<<endl;}cout<<r<<endl;
}