2024.5.18 杂题
「SMOI-R1」Apple
两个操作，修改元素，求子集和。
高位前缀和不会。考虑朴素 dp 转移
设 \(f[i]\) 表示二进制下长度为 \(n\) 的数前 \(i\) 位为 \(1\)，后边为 \(0\) 的子集和。理论来说可以转移，但是比较麻烦，考虑优化状态，\(f[i][j]\) 表示前 \(\frac{n}{2}\) 位为 \(i\) 后 \(\frac{n}{2}\) 位为 \(j\) 的子集和。在插入一个 \(a_i\) 时，枚举前 \(\frac{n}{2}\) 位的超集 \(X\)，令 \(f[X][y] += a_i\) ，删除时减去即可。
在查询 \(i\) 的子集和时，枚举后 \(\frac{n}{2}\) 的子集 \(Y\)，答案 \(\sum_{Y \subseteq y} f[x][Y]\)
这些操作与树状数组很类似，仿照树状数组写一个数据结构优化掉，复杂度大概是 \(O(Q \sqrt{N})\)。
const int N = (1 << 20) + 10;
const int M = (1 << 10) - 1;int n, q;
int a[N];struct Tree
{int c[M + 2][M + 2];void add(int x, int y) {int X = x >> 10, Y = x & M;if (n <= 10) {c[0][Y] += y; return ;}for (rint i = X; i <= M; i = (i + 1) | X) c[i][Y] += y;}int query(int x) {int X = x >> 10, Y = x & M, ans = 0;for (rint i = Y;; i = (i - 1) & Y) {ans += c[X][i];if (!i) break;}return ans;}void clear(int x, int y) {int X = x >> 10, Y = x & M;if (n <= 10) {c[0][Y] -= y; return ;}for (rint i = X; i <= M; i = (i + 1) | X)c[i][Y] -= y;}
} tree;signed main()
{ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);cin >> n >> q;for (rint i = 0; i < (1 << n); i++) {cin >> a[i];tree.add(i, a[i]);}while (q--) {int op, x;cin >> op >> x;if (op == 1) {cout << tree.query(x) << endl;} else {int y;cin >> y;tree.clear(x, a[x]);a[x] = y;tree.add(x, a[x]);}}return 0;
}
『STA - R5』RDG
不会博弈论，考虑 dp
设 \(f_{i,j}\) 表示考虑从 \(a_i\) 到 \(a_n\) 这一段，前面进行了 \(j\) 次 \(1\) 操作的情况下先手能不能赢。\(a\) 需要从小到大排序。
\[f_{i,j}=\begin{cases}1&j>a_i\\f_{i+1,j}&j=a_i\\\neg f_{i+1,j}\operatorname{or}\neg f_{i,j+1} &j<a_i\\\end{cases}
\]
当 \(j\le a_i-2\) 时为 \(01\) 相间。所以保留 \(O(1)\) 状态即可通过本题。
bool c(int i, int j)
{if (i == n || j > a[i]) return 1;if (j < a[i] - 3) j += (a[i] - 2 - j) / 2 * 2;if (!v[i][a[i] - j]) {v[i][a[i] - j] = 1;if (a[i] == j) f[i][a[i] - j] = c(i + 1, j);else f[i][a[i] - j] = !(c(i + 1, j) & c(i, j + 1));}return f[i][a[i] - j];
}signed main()
{int T;cin >> T;while (T--){cin >> n;for (rint i = 1; i <= n; i++) cin >> a[i];for (rint i = 1; i <= n; i++) for (rint j = 0; j <= 3; j++) f[i][j] = v[i][j] = 0;sort(a + 1, a + n + 1);if (c(1, 0)) cout << "Alice" << endl;else cout << "Bob" << endl;}return 0;
}
CF1965E
毒瘤构造，虽然尺子姐已经在题解区给出了构造方案，但我还是想自己去搭一搭，于是找 hanss6 要了个 MC。
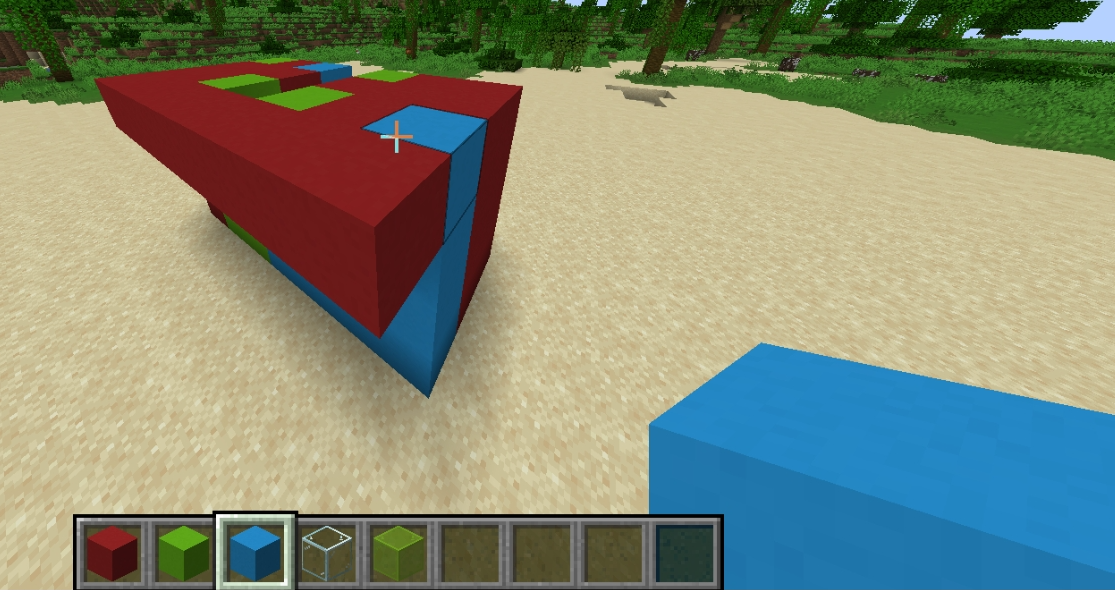
图中玻璃表示临时空气，混凝土即为不同色方块。
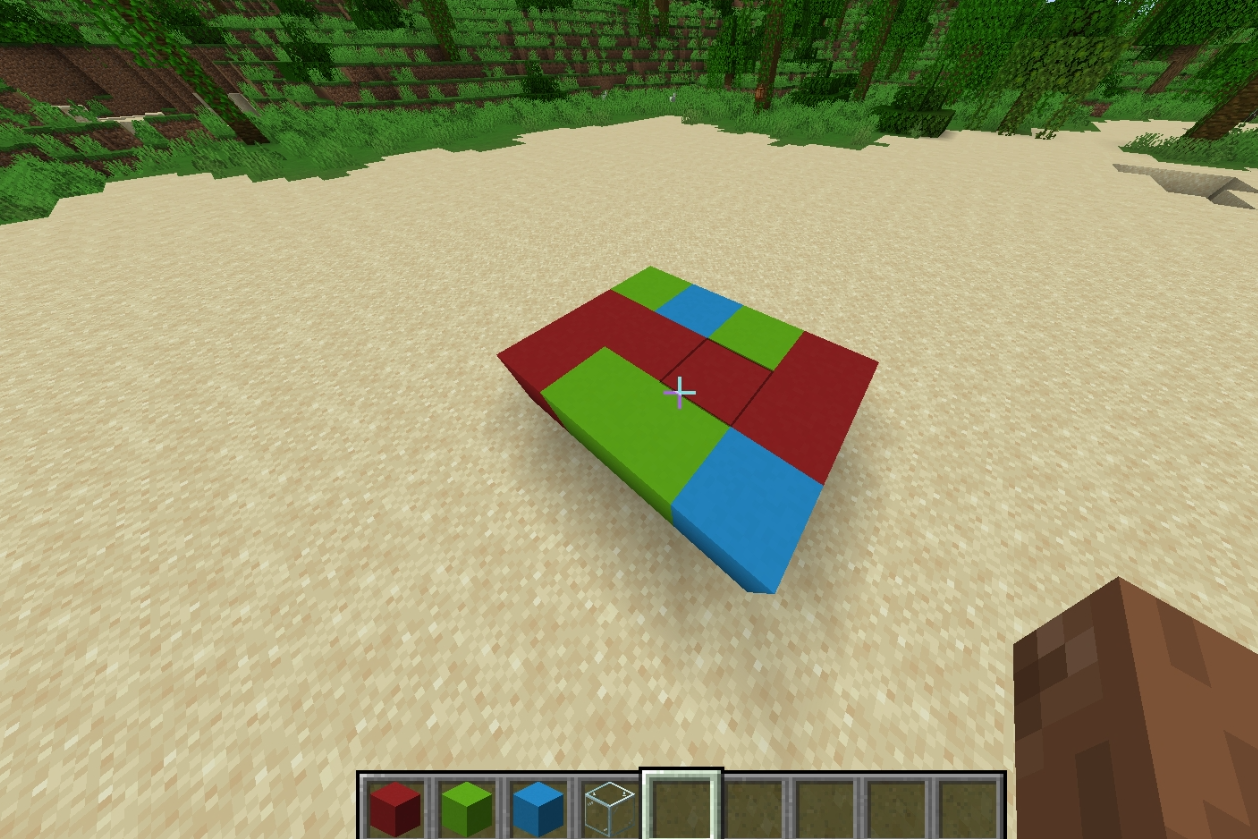
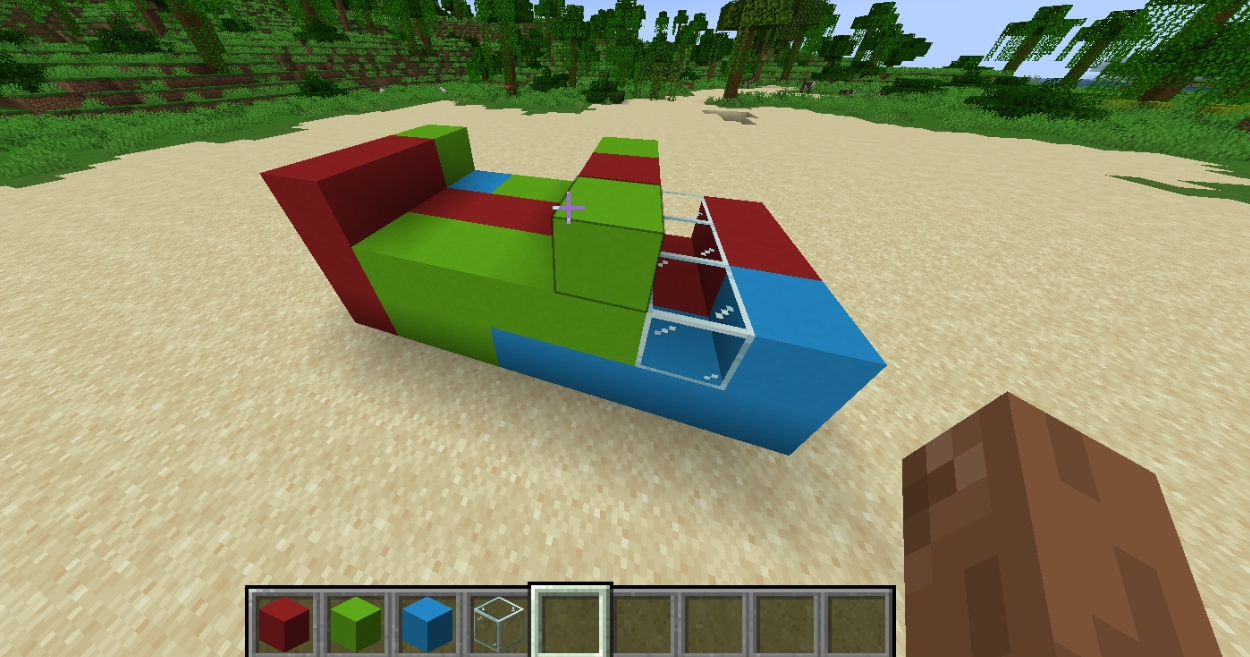
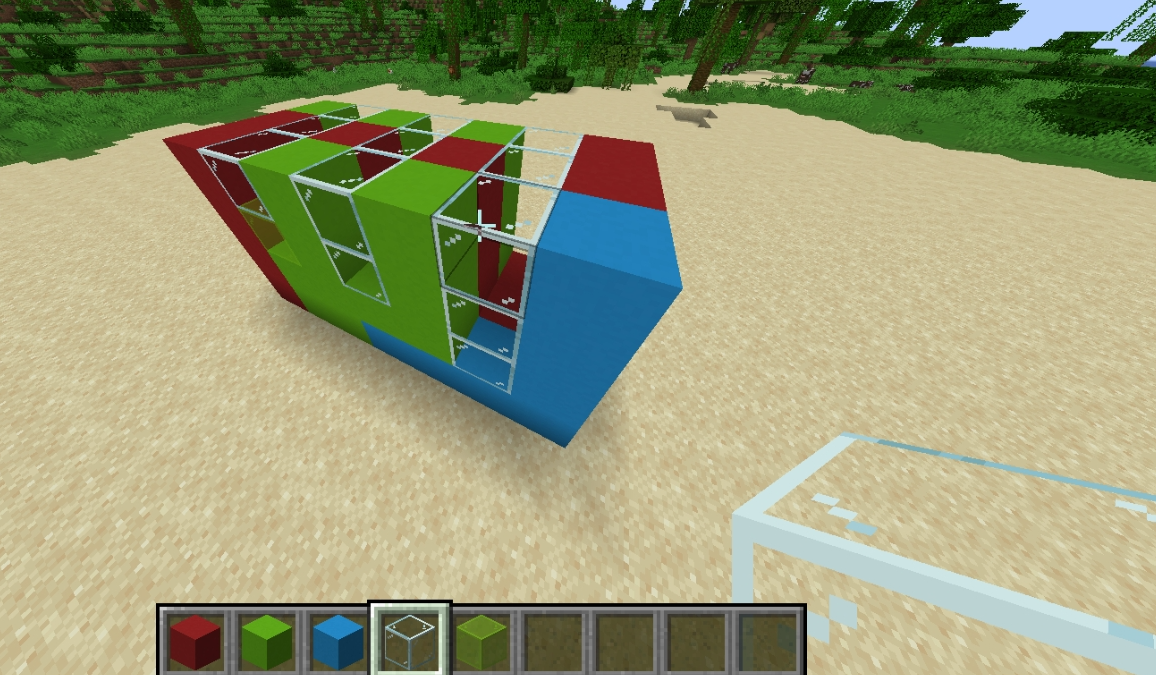
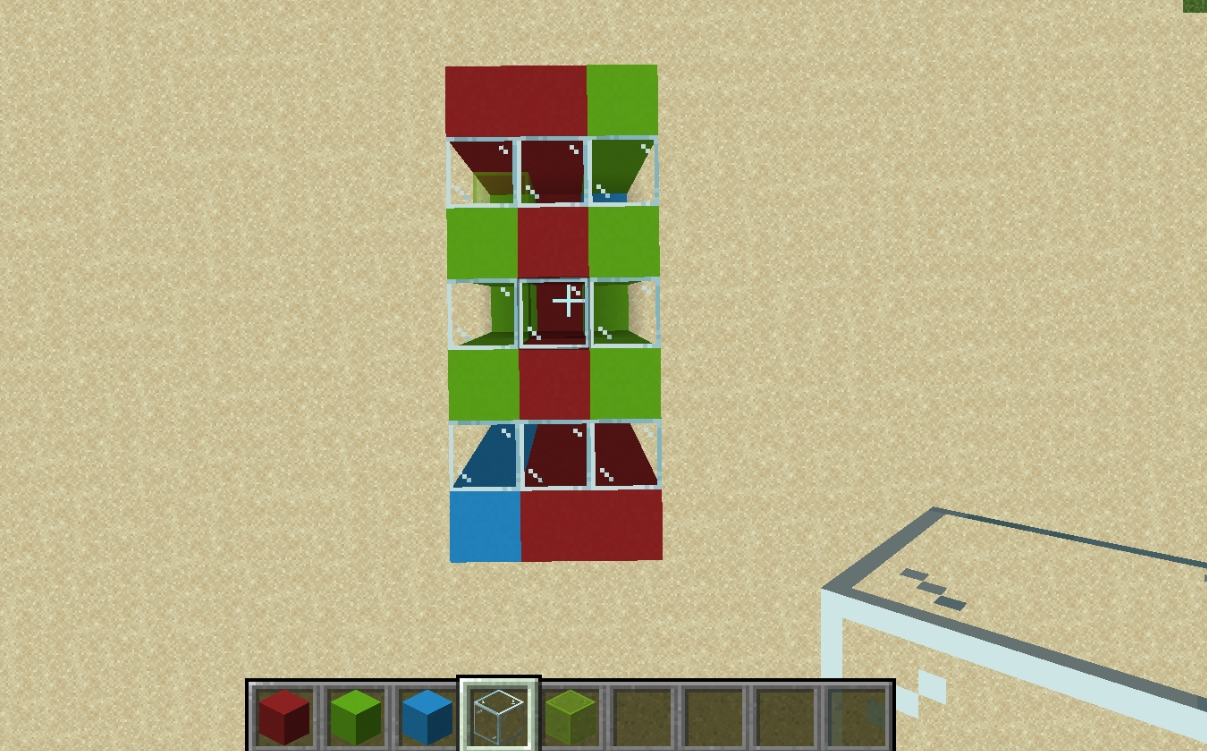
最上层所有混凝土均至少紧挨着一格空气，只需把所有空气替换成一种颜色的混凝土就连通
int n, m, k;
int a[N][N], x[N][N], y[N][N];
vector<tuple<int, int, int, int>> s;signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); cin >> n >> m >> k;for (rint i = 1; i <= n; i++)for (rint j = 1; j <= m; j++)cin >> a[i][j];for (rint i = 1; i <= n; i++){for (rint j = 1; j <= m; j++){x[i][j] = i;y[i][j] = j;}}for (rint z = 1; z <= m; z++){if(z >= 2) {for (rint i = 1; i <= n; i++)for (rint j = 1; j <= m; j++) s.ep(x[i][j], y[i][j], z, a[i][j]);}for (rint i = 1; i <= n; i++)for (rint j = 1; j <= m; j++) {if(j == m - z + 1) {for (rint y = j + 1; y <= 2 * j - 1; y++)s.ep(i, y, z, a[i][j]);x[i][j] = i;y[i][j] = 2 * j - 1;}}}int _m = m;for (rint p = 1; p <= k; p++){for (rint i = 1; i <= n + 1; i++) {for (rint j = 1; j <= 2 * m - 1; j++) {if (i == n + 1) s.ep(i, j, _m, p);else if (j % 4 == 2 || j >= 2 * m - 3 && !(j % 2)) s.ep(i, j, _m, p);else if ((j & 1) && _m != m && a[i][(j + 1) / 2] >= p) s.ep(i, j, _m, a[i][(j + 1) / 2]);}}_m++;}cout << s.size() << endl;for (auto it : s){cout << get<0>(it) << " ";cout << get<1>(it) << " ";cout << get<2>(it) << " ";cout << get<3>(it) << endl;}return 0;
}
饥饿的奶牛
考虑直接枚举每一个点。设 \(f[i]\) 为从开始到 \(i\) 时的答案。用 vector 存区间。对于区间 \(a_i\) 有
\[f[s_i.r] = \max_{0≤j≤s_i.l}{\{}f[j]\}
\]
int n;
int f[N];
vector<int> a[N];signed main()
{cin >> n;for (rint i = 1; i <= n; i++){int x, y;cin >> x >> y;a[y].push_back(x);}for (rint i = 0; i <= M; i++){f[i] = f[i - 1];int k = a[i].size();for (rint j = 0; j < k; j++){int val = i - a[i][j] + 1;if (a[i][j] >= 1) f[i] = max(f[i], f[a[i][j] - 1] + val);else f[i] = max(f[i], val);}}cout << f[M] << endl;return 0;
}
