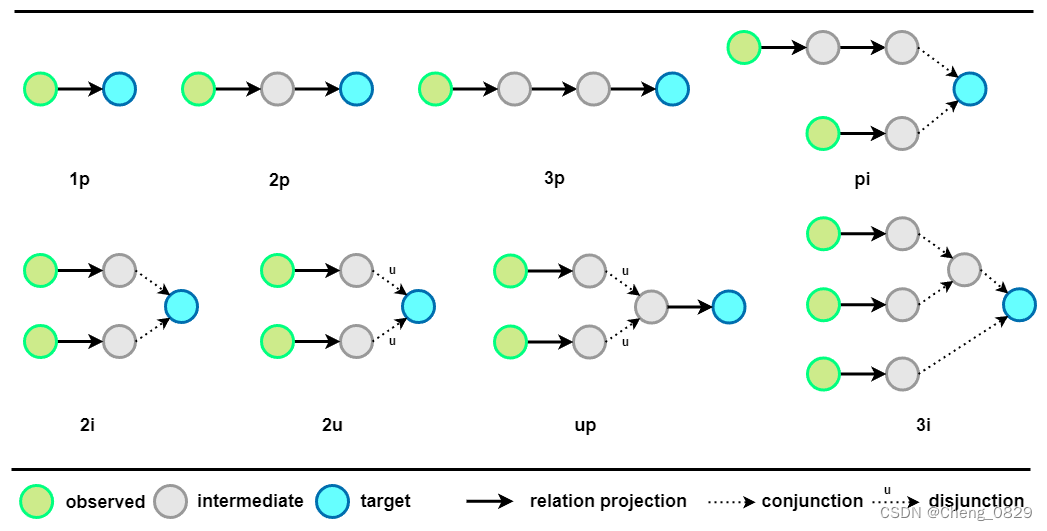
贝叶斯推断基础
贝叶斯方法提出了一个概率框架来描述如何将新的观察结果整合到决策过程中。传统的贝叶斯推断的二进制算术结构中,后验概率的计算需要大量的乘、除、加。
先验概率(由历史求因):根据以往经验和分析得到的概率,观测数据前某一不确定量的先验概率分布,通常指模型的参数\(\theta\)对应的\(P(\theta)\)
后验概率(知果求因):一个随机事件或者一个不确定事件的后验概率是在考虑和给出相关证据或数据后所得到的条件概率。这个概率需要观测数据才能得到,对一个神经网络建模需要基于给定的数据集才能得到网络参数\(\theta\)。后验概率表示为\(P(\theta|X)\)。
似然函数(由因求果):一种关于统计模型参数的函数。给定输出\(x\)时,参数\(\theta\)的似然函数\(L(\theta|x)\)等于给定参数\(\theta\)后变量\(X\)的概率。\(L(\theta|x)=P(X=x|\theta)\)。
二分类贝叶斯机器(Bayesian Machine)
给定类别\(V_1,V_2\),有\(Pr(V_1)+pR(V_2)=1\),\(Pr(V_1),Pr(V_2)\)为后验概率。假设有\(M\)个特征证据,\(E_1,E_2,\cdots,E_M\)。对给定集合的特征,\(E_1,E_2,\cdots,E_M\)满足条件独立,类别\(V_1\)的后验概率为:\(P_r(V_1|E_1,E_2,\cdots, E_K)=\frac{Pr(V_1)\prod_{j=1}^K Pr(E_j|V_1)}{Pr(V_1)\prod_{j=1}^K Pr(E_j|V_1)+Pr(V_2)\prod_{j=1}^K Pr(E_j|V_2)}\)
双权重加权比的SC实现
令\(Pr(V_i)=\omega_i\)和\(Pr(E_j|V_i)=\theta_{ij}\),其中\(i=1,2\)和\(j=1,2,\cdots,K\),类别\(V_1\)关于两个权重\(\omega_1,\omega_2\)的加权比的后验概率为:\(z=\frac{\omega_1\theta_1}{\omega_1\theta_1+\omega_2\theta_2}\)(\(\omega_1+\omega_2=1,\theta_i=\prod_{j=1}^K\theta_{ij}\)),令\(\theta_{1j}^{*}=\frac{\theta_{1j}}{\theta_{1j}+\theta_{2j}}\),可以进步表示为\(z=\frac{\omega_1 \prod_{j=1}^K \theta_{1j}^*}{\omega_1\prod_{j=1}^K\theta_{1j}^*+(1-\omega_1)\prod_{j=1}^K(1-\theta_{1j}^*)}\)。
MULLER-C ELEMENT
Celement
Mulle-C Element通常由四个与非门组成,包含两个输入端和一个输出端。
\(C=(ab|bc|ac)\)
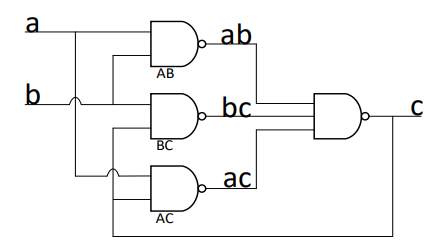
当\(a,b\)输入端均为0时,输出端将变化为0。当两者的输出为1时,输出端为1;其余情况,输出保持不变。