A - Exponential Plant (abc354 A)
题目大意
某星球上的植物,初始高\(0\),然后每天依次增长 \(1,2,4,8,...\),问哪天就高过身高为\(h\)的高桥。
解题思路
因为是指数级别长高,枚举一下天数即可,由于\(h \leq 10^9\),因此天数不会超过 \(32\)天。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;int main(void) {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int x;cin >> x;++x;int cnt = 0;while (x) {cnt++;x >>= 1;}cout << cnt << '\n';return 0;
}B - AtCoder Janken 2 (abc354 B)
题目大意
给定\(n\)个人的名字和分数。
按名字字典序给他们排序。
然后设他们总分数为 \(sum\),则第 \(sum % n\)位为赢家。
问谁是赢家。
解题思路
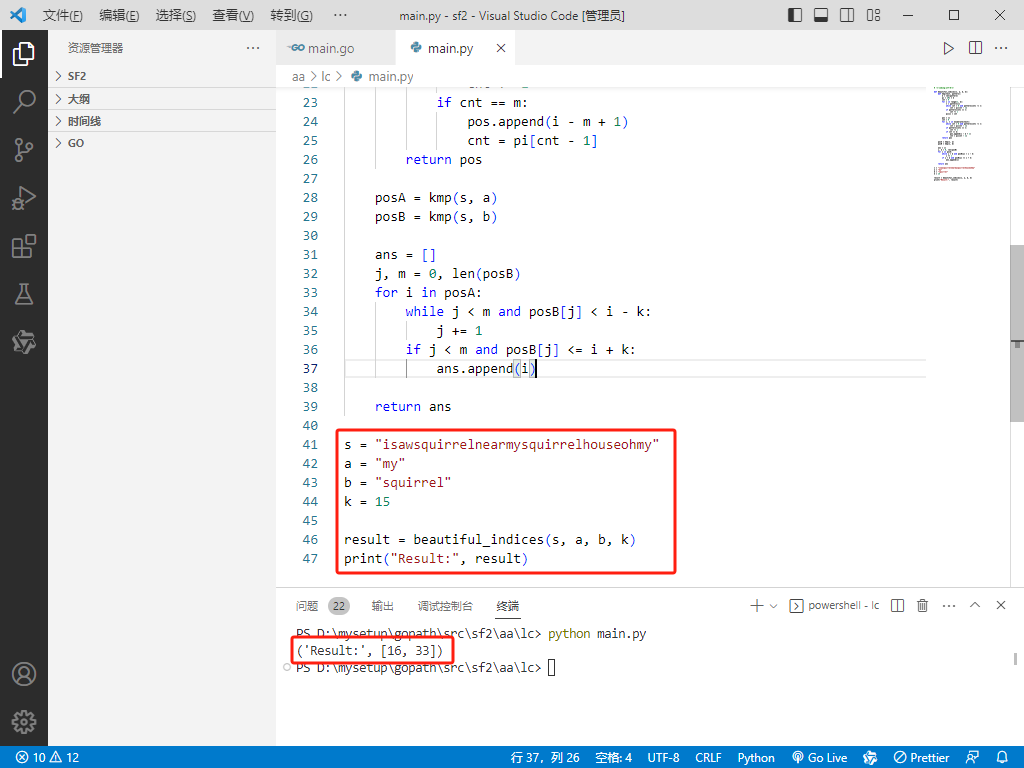
按照题意,给名字排序,对分数求和,取个模后找到对应人的名字即为答案。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;int main(void) {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n;cin >> n;int sum = 0;vector<pair<string, int>> a(n);for (auto& i : a) {cin >> i.first >> i.second;sum += i.second;}vector<int> id(n);iota(id.begin(), id.end(), 0);sort(id.begin(), id.end(),[&](int i, int j) { return a[i].first < a[j].first; });int win = id[sum % n];cout << a[win].first << '\n';return 0;
}C - AtCoder Magics (abc354 C)
题目大意
\(n\)个卡牌,有对应的强度\(a_i\)和花费 \(c_i\)。
对于两个卡牌 \(i,j\),如果 \(a_i > a_j\)且 \(c_i < c_j\),则卡牌 \(j\)会被丢弃。
不断进行如上操作,问最终的牌是哪些。
解题思路
对每个卡牌的代价\(c\)从小到大排序,然后依次考虑当前卡牌\(j\)是否要丢弃。
因为是按顺序枚举 \(j\),则 \(i < j\)的卡牌都满足 \(c_i < c_j\),如果存在\(a_i > a_j\),则说明当前卡牌要丢弃。
因为是存在,所以我们维护 \(\max_{1 \leq i < j}(a_i)\),一个前缀的强度最大值,如果 \(max_a > a_j\),说明当前卡牌 \(j\)要丢弃,否则就不用丢弃。
把不需要丢弃的卡牌放到一个数组里,然后输出即可。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;int main(void) {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n;cin >> n;vector<array<int, 2>> a(n);for (auto& x : a)cin >> x[0] >> x[1];vector<int> id(n);iota(id.begin(), id.end(), 0);sort(id.begin(), id.end(), [&](int i, int j) { return a[i][1] < a[j][1]; });vector<int> ans;int maxx = 0;for (auto x : id) {if (a[x][0] < maxx)continue;ans.push_back(x);maxx = max(maxx, a[x][0]);}cout << ans.size() << '\n';sort(ans.begin(), ans.end());for (auto x : ans) {cout << x + 1 << " ";}cout << '\n';return 0;
}D - AtCoder Wallpaper (abc354 D)
题目大意
给定一个如下定义的二维网格。

给定一个矩形区域,问该区域的黑色部分面积的两倍是多少。
解题思路
非常好的图,让我不知所措
定眼一看,发现只有本质不同的两类行(注意图里的水平线仅在\(y\)是偶数的行),每行的形状具有循环节,循环节长度为\(4\)。
因此我们只需考虑考虑两行,最多长度为\(3\)的区域,其余的面积可以直接通过循环节算出来。
一个是偶数行(\(y = 0 \to 1\)),从 \((0,0)\)来往\(x\)正方向看, 循环节为\(4\)的黑色面积的两倍分别为 \(2, 1, 0, 1\)。奇数行则为\(1, 2, 1, 0\)。
因此矩形区域\((a,b) -> (c,d)\) ,考虑\(a \to c\)的偶数行,可以计算出其黑色面积的大小,一个是循环节的大小 \(\lfloor \frac{c - a}{4} \rfloor \times (2 + 1 + 1)\),然后是多余的一小部份长度\((c - a) \% 4\),这个直接暴力计算即可。然后再\(\times\)偶数行的数量。
同理计算出奇数行的面积大小\(\times\)奇数行的数量,两者的和即为答案。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;int main(void) {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int a, b, c, d;cin >> a >> b >> c >> d;array<array<int, 4>, 2> area{{{2, 1, 0, 1}, {1, 2, 1, 0}}};int sum = 4;auto solve = [&](int odd, int l, int r, int h) {LL ss = 1ll * (r - l) / 4 * sum * h;int cnt = (r - l) % 4;while (cnt--) {int left = ((l % 4) + 4) % 4;ss += 1ll * area[odd][left] * h;l++;}return ss;};int odd = (abs(b) % 2);LL one = solve(odd, a, c, (d - b + 1) / 2);LL two = solve(odd ^ 1, a, c, (d - b) / 2);cout << one + two << '\n';return 0;
}E - Remove Pairs (abc354 E)
题目大意
给定\(n\)张卡牌,每张卡牌正反各写一个数字,高桥和青木玩游戏,每回合,一个人可拿走两张正面数字一样或反面数字一样的卡牌。不能操作者人输。
高桥先,问两者绝顶聪明的情况下,谁赢。
解题思路
朴素的博弈\(dp\)。由于 \(n \leq 18\),可以直接设 \(dp[i]\)表示现在还有的卡牌情况(一个二进制压缩状态)是\(i\)的情况下,先手是必赢还是必输。
要看其是必输还是必赢,则需要看后继状态是否存在必输态,如果存在必输态,则当前状态\(i\)可以通过对应的转移变成先手必输态 \(j\)(从当前态 \(i\)来看就是后手必输了),则说明当前状态 \(i\)是必赢,即 \(dp[i] = 1\),否则如果所有后继状态都是必赢态,则说明当前是必输态,即 \(dp[i] = 0\)。
而后继状态就是当前状态可以做的决策的转移,即选择两张正面数字一样或反面数字一样的卡牌拿走。花\(O(n^2)\)枚举下选择的两张牌即可。
总的时间复杂度是 \(O(n^22^n)\)
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;int main(void) {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n;cin >> n;vector<array<int, 2>> a(n);for (auto& x : a)cin >> x[0] >> x[1];int up = (1 << n);vector<int> dp(up, -1);dp[0] = 0;auto dfs = [&](auto dfs, int s) -> int {if (dp[s] != -1)return dp[s];int ok = 0;for (int i = 0; i < n; i++) {if ((~s >> i) & 1)continue;for (int j = i + 1; j < n; j++) {if ((~s >> j) & 1)continue;if (a[i][0] != a[j][0] && a[i][1] != a[j][1])continue;ok |= !dfs(dfs, s ^ (1 << i) ^ (1 << j));}}return dp[s] = ok;};int ok = dfs(dfs, up - 1);if (ok) {cout << "Takahashi" << '\n';} else {cout << "Aoki" << '\n';}return 0;
}F - Useless for LIS (abc354 F)
题目大意
给定一个数组\(a\)。
对于每个数字 \(a_i\),问在\(a\)的最长上升子序列中,\(a_i\)是否存在其中。
多组询问。
解题思路
首先肯定要求一遍最长上升子序列的长度,由于\(n \leq 2e5\),得用\(O(n \log n)\)的求法,假设我们求得的长度是\(LIS\)。
考虑如何判断 \(a_i\)是否存在最长上升子序列中。
考虑最朴素的求上升子序列的求法,即 \(dp[i]\)表示前 \(i\)个数字,我选择第\(i\)个数字的最长上升子序列的长度,转移则枚举上一个数字是哪个。
如果\(a_i\)可以成为最长上升子序列中,那说明什么?
我 \(1 \to i\)中,选择 \(a_i\),得到最长上升序列长度 \(dp[i]\), 如果它可以成为最长上升子序列,则说明\(i \to n\)的最长上升子序列长度是 \(LIS - dp[i] + 1\)。这相当于从右往左考虑的最长下降子序列 \(dp_2[i] = LIS - dp[i] + 1\)。
因此我们只需要求出从左到有的最长上升子序列长度\(dp[i]\)和从右往左的最长下降子序列长度 \(dp_2[i]\)。然后对于每个 \(a_i\),如果 满足 \(dp[i] + dp_2[i] - 1 == LIS\),则说明 \(a_i\)会存在 \(a\)的最长上升子序列中。
那现在的问题就是如何求\(dp\)和 \(dp2\),朴素的 \(dp\)的求法是 \(O(n^2)\),对于这里的 \(n \leq 2e5\)会超时。
考虑 \(O(n \log n)\)的求法,事实上可以从这还原出\(dp\)。
即 \(len[i]\)表示最长上升子序列长度为 \(i\)的末尾数字(最大数字)的最小值。(和上面的区别相当于把 \(dp\)的值作为状态,条件变成了值),注意到 \(len\)是一个递增的数组,因此对于当前数字\(a_i\) ,可以二分找到它可以接在哪个数字\(a_j\)的后面,进而知道了当前的\(dp[i]\),然后更新 \(len\)数组。
代码中求 \(dp2\)是将 \(a\)左右翻转然后全部取相反数,就相当于再求一个从左到右的最长上升子序列了。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;const int inf = 1e9 + 7;int main(void) {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t;cin >> t;while (t--) {int n;cin >> n;vector<int> a(n);for (auto& x : a)cin >> x;int LIS = 0;auto solve = [&](vector<int>& a) -> vector<int> {vector<int> dp(n + 1, inf), len(n, 1);dp[0] = -inf;for (int i = 0; i < n; ++i) {int pos = lower_bound(dp.begin(), dp.end(), a[i]) - dp.begin();len[i] = pos;dp[pos] = min(dp[pos], a[i]);LIS = max(LIS, pos);}return len;};auto l = solve(a);reverse(a.begin(), a.end());for (auto& i : a)i *= -1;auto r = solve(a);reverse(r.begin(), r.end());vector<int> ans;for (int i = 0; i < n; ++i) {if (l[i] + r[i] - 1 == LIS)ans.push_back(i + 1);}cout << ans.size() << '\n';for (auto x : ans)cout << x << ' ';cout << '\n';}return 0;
}G - Select Strings (abc354 G)
题目大意
给定\(n\)个字符串。字符串有价值。
选定一些字符串,使得字符串俩俩之间不存在子串的关系,最大化价值。
解题思路
首先可以花\(O(\max(n^2, (\sum |s|)^2))\) 求出俩俩字符串之间的不可选择关系。
剩下的问题就是有一个图,点有点权,点之间的连边表示不能同时选。然后选些点,点权值最大。
感觉很像一个最小割
神奇的代码