[ABC354D]

https://www.luogu.com.cn/problem/AT_abc354_d

https://atcoder.jp/contests/abc354/tasks/abc354_d

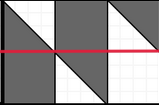
由图片可知，很显然每个 \(4\times 2\)​ 网格（称为单位网格）都是全等的。

为了方便，将 \(A,B,C,D\) 都增加 \(10^9\)，因为 \(10^9\bmod 4=10^9\bmod 2=0\)，所以图形没有变化。（很重要，这样就很明显只有 \(8\) 种分讨的情况了）。

以下面积指 \(\times 2\)​ 后的值（即答案）。

然后我们利用前缀和技巧即可求出 \((A,B)\) 到 \((C,D)\) 的面积。

设 \(S(x,y)\) 表示 \((0,0)\) 到$ (x,y)$ 的面积。

于是考虑根据 \(a=x\bmod 4,b=y\bmod 2\) 的情况大力分讨：

1. \(b=0\)（直接运算的方法）

   1. \(a=0\)，刚好是若干个单位网格，\(S=x\times y\)（单位网格内所有黑色、白色成对出现）
   2. \(a=1\)，刚好是若干个单位网格+往右扩展 \(dy\div 2\) 个，\(S=(x-1)\times y+y\div 2\times 3\)。
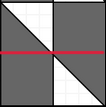   3. \(a=2\)，刚好是若干个单位网格+往右扩展 \(dy\div 2\) 个，\(S=(x-2)\times y+y\div2\times 6\)。
   4. \(a=3\)，刚好是若干个单位网格+往右扩展 \(dy\div 2\) 个，\(S=(x-3)\times y+y\div2\times 7\)。

2. \(b=1\)​（利用前缀和）

   1. \(a=0\)，发现多出来的一行恰好是若干个半个单位网格，\(S==(x-1)\times y+x\)。
   2. \(a=1,2,3\)，直接利用前缀和加上右上角的网格的面积（分别是，\(+2,1,0\))。（计算按照 \(a=0,1,2,3\) 的顺序，因为每次要利用 \(S(x,y-1)\))。

时间复杂度 \(O(1)\)​。

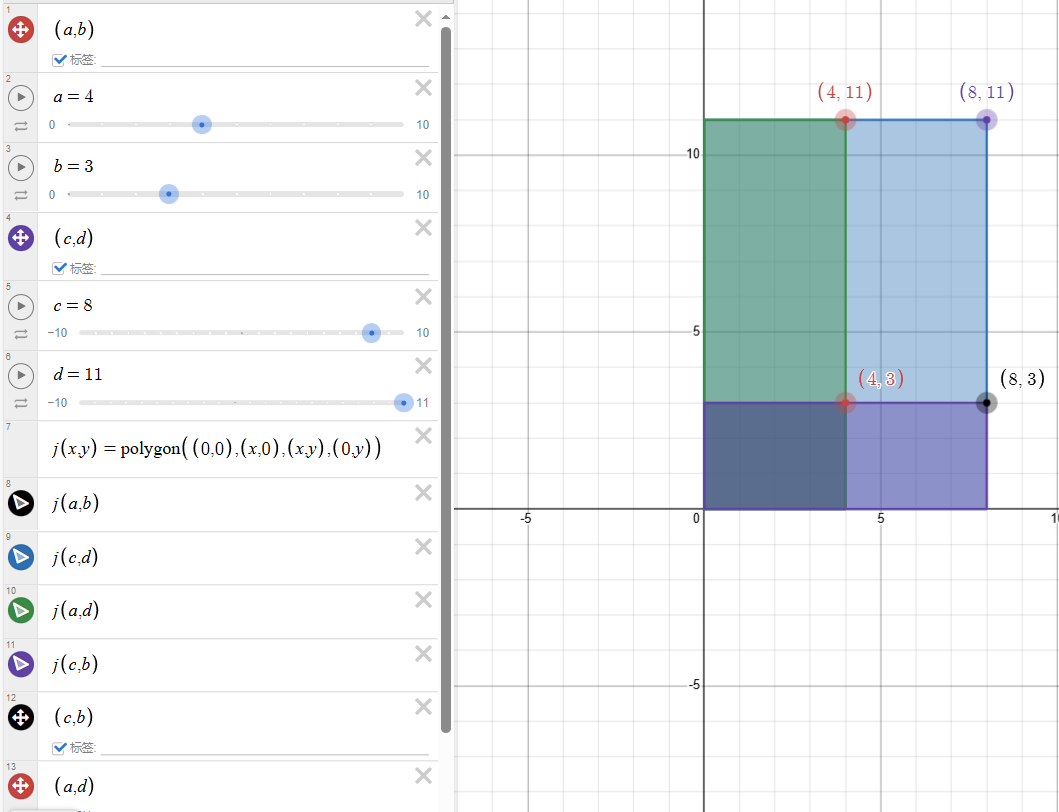
如图，\(S(A,B,C,D)=S(C,D)-S(A,D)-S(C,B)-S(A,B)\)。

根据上图也可以解释上述分讨第2大类的求前缀和： \(S(A,B)=S(A-1,B)+S(A,B-1)-S(A-1,B-1)+\text{val(A,B)}\)。

https://atcoder.jp/contests/abc354/submissions/53651499