🌟个人博客：www.hellocode.top
🏰Java知识导航：Java-Navigate
🔥CSDN：HelloCode.
🌞知乎：HelloCode
🌴掘金：HelloCode
⚡如有问题，欢迎指正，一起学习~~

---

希尔排序是一种插入排序的改进版本，旨在解决插入排序在处理大规模数据时的效率问题。通过将数组分为多个子序列并对这些子序列进行局部排序，希尔排序逐步将元素“分组”并逐渐接近它们的最终排序位置。这种逐步的排序方式可以有效减少逆序对的数量，从而加快整体排序过程。

基本思想

这里使用五分钟学算法大佬的动图，很清晰

1. 希尔排序将数组分成若干个子序列，每个子序列包含间隔为 h 的元素，称为 h-子序列。
2. 对每个 h-子序列应用插入排序，以实现局部排序。
3. 不断缩小 h 的值，重复步骤 2，直到 h 为 1。此时，整个序列基本有序，只需对相邻元素进行插入排序即可。

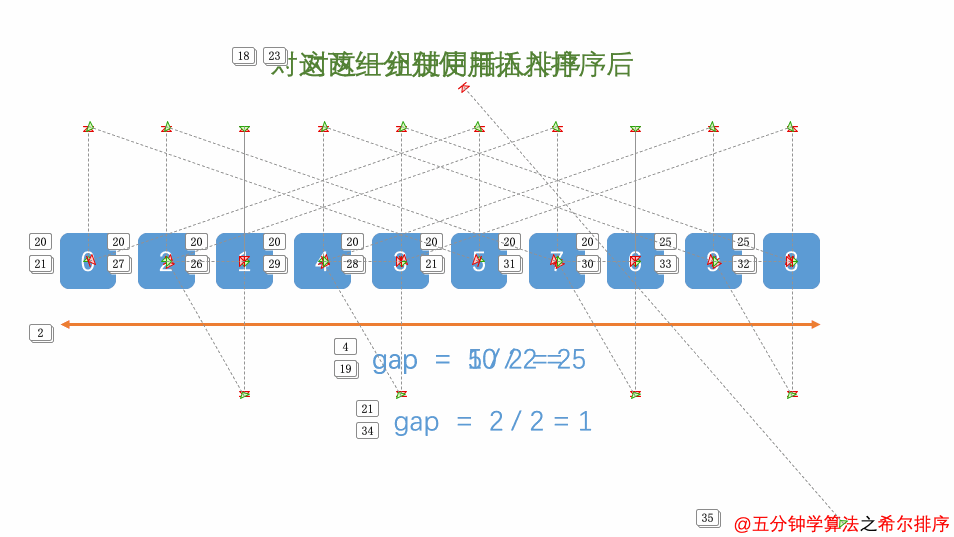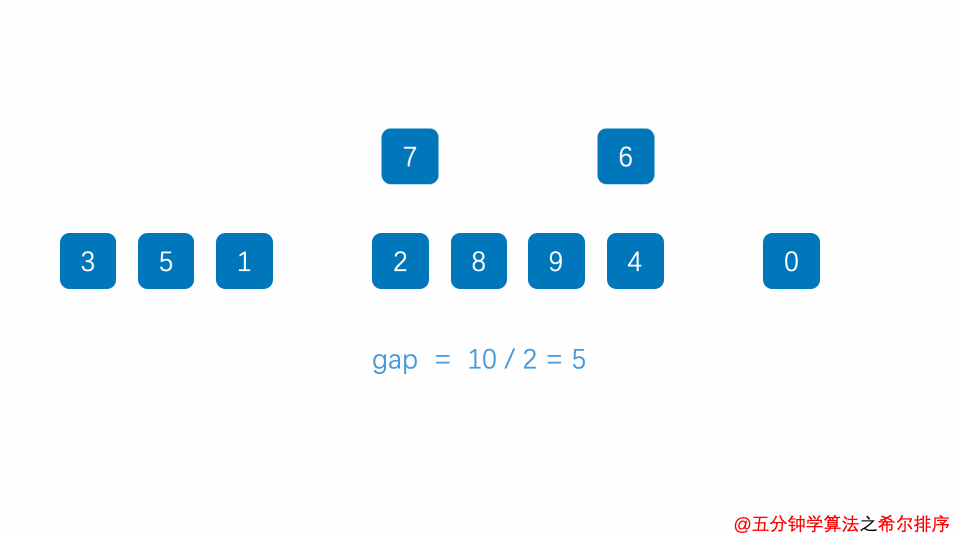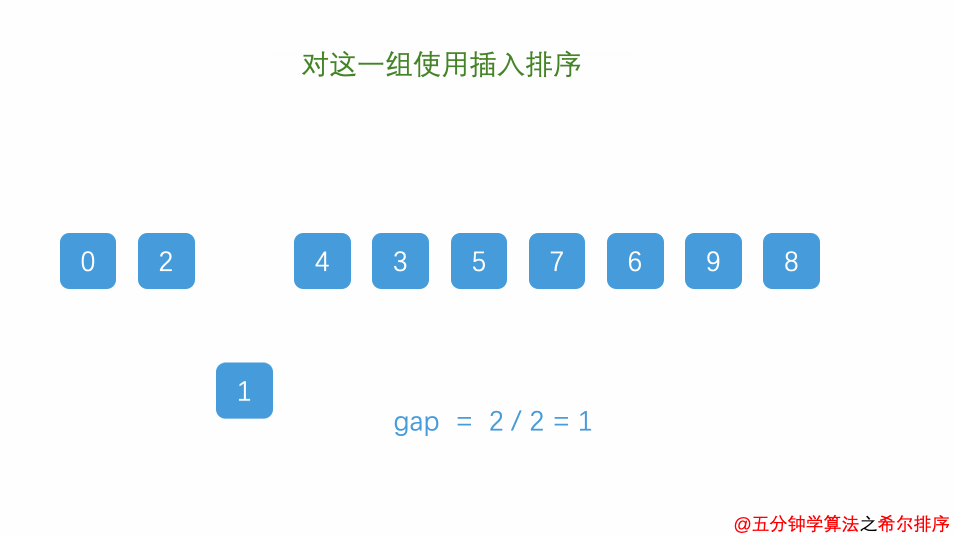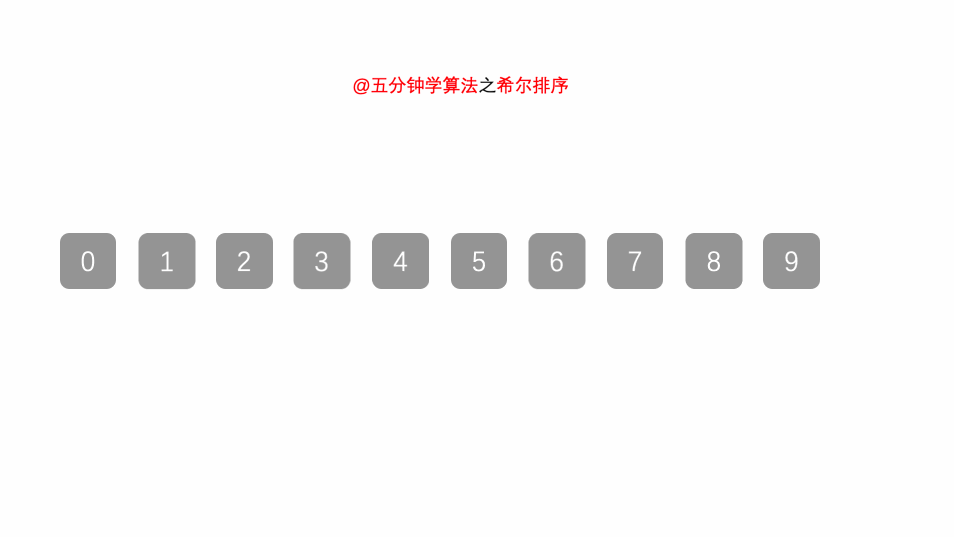
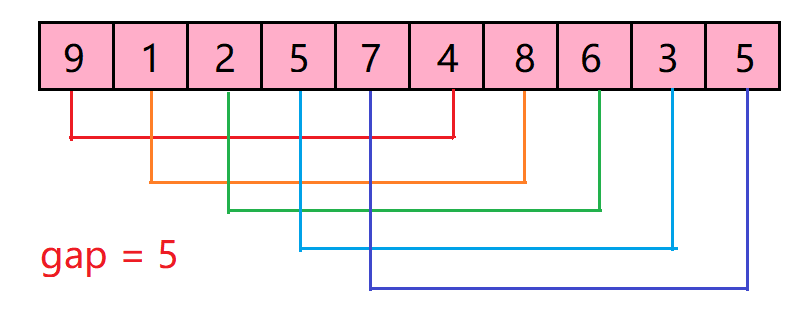
一般间隔也就是gap的选取就是数组长度的一半，如上图所示，原始数组为[8,9,1,7,2,3,5,4,6,0]，初始间隔就是5，也就是会将图中数组分为[8,3]、[9,5]、[1,4]、[7,6]、[2,0]共5组，然后对这些组合进行插入排序，并不断缩小gap（每次缩小一半），重复进行插入排序操作，最终就能够得到有序数组~

对分组不太理解的可以看下图，非常清晰：

代码实现

代码的话还是循环，只需要在插入排序外层再加一层循环控制gap 的缩小即可，就是改良版的插入排序（需要对比图片和插入排序的思路仔细体会），具体代码如下：

/*** @author HelloCode* @blog https://www.hellocode.top* @date 2023年08月10日 20:59*/
public class ShellSort {public static void main(String[] args) {int[] arr = {8,9,1,7,2,3,5,4,6,0};System.out.println("原数组：" + Arrays.toString(arr));shellSort(arr);System.out.println("排序后：" + Arrays.toString(arr));}public static void shellSort(int[] arr){int n = arr.length;// 两层for循环，外层不断缩小gap(每次缩小为一半)for(int gap = n / 2; gap > 0; gap /= 2){// 内层对每组进行插入排序// 这里的i还是指向第一个待插入元素(也就是gap，可以看图理解)// 此时已排序数组的最后一个元素，就应该是i - gap// 这里i的跨度就不应该是++而是 += gap（配合图更好理解）for(int i = gap;i < n; i ++){int current = arr[i];       // 当前待插入元素int pre = i - gap;          // 有序部分的最后一个元素下标// 当 i 位置元素大于等于 pre 位置元素时说明已经有序，就继续i+= gapwhile(pre >= 0){// 已经是正确位置，直接退出循环if(current >= arr[pre]){break;}// 位置不正确，需要寻找正确位置arr[pre + gap] = arr[pre];pre -= gap;}//此时pre下标的值是负数了，将current的值放到pre变量加上一个gap的位置上arr[pre + gap] = current;}}}
}

测试：

原数组：[8, 9, 1, 7, 2, 3, 5, 4, 6, 0]
排序后：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

优化

• 希尔排序的性能高度依赖于步长序列的选择。选择不同的步长序列可能会对排序效率产生影响。
• 一些常见的步长序列包括希尔步长序列（h = n/2, n/4, n/8, …）、Sedgewick步长序列等。
• 通过尝试不同的步长序列，可以选择合适的步长来优化希尔排序的性能。

总结

优点

1. 相对于传统的插入排序，希尔排序通过将元素分组进行排序，减少了逆序对的数量，从而加快了排序过程。
2. 希尔排序是原地排序算法，只需在原始数组上进行元素的交换和移动，不需要额外的辅助空间。

缺点

1. 希尔排序的最坏情况时间复杂度并不稳定，通常在 O(n^2) 到 O(n log n) 之间。虽然平均情况下性能较好，但在某些特定情况下，性能可能不如其他高级排序算法。
2. 步长序列的选择对性能产生影响，选择不当可能导致排序效率下降。

复杂度

• 时间复杂度：取决于步长序列的选择，通常在 O(n log n) 到 O(n^2) 之间。
• 空间复杂度：原地排序，空间复杂度为 O(1)。

使用场景

1. 希尔排序适用于中等规模的数据集，对于大规模数据，其性能可能不如其他更高级的排序算法。
2. 在实际应用中，希尔排序的性能可能会比预期的好，尤其在某些特定情况下，例如对部分有序的数据进行排序时。

当使用希尔排序时，应特别注意其时间和空间复杂度的说明是基于最坏情况下的估计。这样的估计可能会高于实际情况。希尔排序在某些实际应用中可能表现得比预期的要好。