SVM

idea of SVM

分类问题的简化

首先我们考虑这样一个分类问题

• 二分类
• 线性分类边界
• 100% 可分

我们就能够考虑想出一个好的 idea，如下图所示

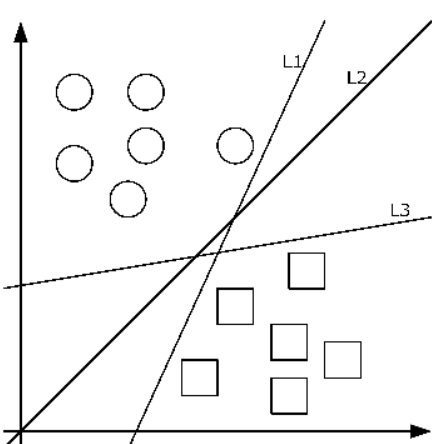
在上述条件满足的情况下，哪一个分类边界最好？

idea：最大化所有点到分类边界的最小距离，这个最小距离称为 margin。

形式化距离

函数间隔：\(| w^Tx_i + b |\)

几何间隔：\(\frac{|w^Tx_i + b|}{\| w \|}\), 这也表示了一个点到超平面的距离

proof

我们 denote \(w^Tx + b = 0\)为超平面，那么对于任意一个点\(x_i\)，我们可以将其投影到超平面上，得到\(x_i'\)，那么有\(r = x_i - x_i' = r_0 w \Rightarrow x_i' = x_i - r_0 w\)

那么有

\[\begin{aligned} r_0 &= \frac{w^T x_i + b}{\| w \|} \end{aligned} \]

\(r_0\)的 abs 即为我们想要的距离

proof end

形式化想法

我们使用几何间隔来表示点到超平面的距离，那么 margin 即为

\[\text{margin}=\min_{i=1,2,\ldots,N} \frac{|w^Tx_i + b|}{\| w \|} \]

如果我们将标签\(y\)限制在集合\(\{ +1, -1 \}\)(为了方便优化),那么我们的目标函数即为

\[\max_{w,b} \min_{i=1,2,\ldots,N} \frac{|w^Tx_i + b|}{\| w \|} \\ \text{s.t. } y_i(w^Tx_i + b) \geq 0, \quad i = 1, 2, \ldots, N \]

去除绝对值，我们可以得到

\[\max_{w,b} \frac{1}{\| w \|} \min_{i=1,2,\ldots,N} y_i({w^Tx_i + b}) \\ \text{s.t. } y_i(w^Tx_i + b) \geq 0, \quad i = 1, 2, \ldots, N \]

形式上依旧可以简化，一个想法是对于一个分式，我们可以通过限制其中一项，来优化另一项，可以得到相同的解，即

\[\arg \max \frac{f(x)}{g(x)} \iff \arg \max \frac{c f(x)}{c g(x)} \iff \arg \max f(x), \quad s.t. \ g(x) = c \]

于是我们可以通过限制 margin 的值，来优化 \(w, b\)，即限制\(\min_{i=1,2,\ldots,N} y_i({w^Tx_i + b}) = 1\)

于是我们可以得到最终形式

\[\min_{w,b} \frac{1}{2} \| w \|^2 \\ \text{s.t. } y_i(w^Tx_i + b) \geq 1, \quad i = 1, 2, \ldots, N \]

这是一个凸二次规划问题，Dual Gap 为 0，因此我们可以通过求解对偶问题来求解原问题，即使用 KKT 条件来求解原问题。

然而值得注意的是，使用对偶问题的好处在于我们能够使用 Kernel function 将原问题映射到高维空间，从而解决线性不可分的问题，对于求解时间的提升并不明显，甚至于说，对于线性可分的问题，我们可以直接求解原问题，而不需要使用对偶问题（\(\mathcal{O}(n^{1.x})\)）。

Hard Margin-SVM

\[\max_{\alpha} \min_{w,b} \frac{1}{2} \| w \|^2 + \sum_{i=1}^N \alpha_i (1 - y_i(w^Tx_i + b)) \\ \text{s.t. } \alpha_i \geq 0, \quad i = 1, 2, \ldots, N \]

\[\begin{aligned} \mathcal{L}(w, b, \alpha) &= \frac{1}{2} \| w \|^2 + \sum_{i=1}^N \alpha_i (1 - y_i(w^Tx_i + b)) \end{aligned} \]

求一下偏导数（最小值的必要条件）:

\[\begin{aligned} \frac{\partial \mathcal{L}(w, b, \alpha)}{\partial w} &= w - \sum_{i=1}^N \alpha_i y_i x_i = 0 \\ \Rightarrow w & = \sum_{i=1}^N \alpha_i y_i x_i \\ \frac{\partial \mathcal{L}(w, b, \alpha)}{\partial b} &= -\sum_{i=1}^N \alpha_i y_i = 0 \\ \end{aligned} \]

代入 \(w, b\)，我们可以得到对偶问题

\[\mathcal{L}(w, b, \alpha) = \frac{1}{2} \| w \|^2 + \sum_{i=1}^N \alpha_i (1 - y_i(w^Tx_i + b)) = \\ \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum_{i=1}^N \alpha_i - \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j = \\ \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j \]

因此，我们可以得到对偶问题

\[\max_{\alpha} \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j \\ \text{s.t. } \alpha_i \geq 0, \quad i = 1, 2, \ldots, N \\ \sum_{i=1}^N \alpha_i y_i = 0 \]

我们如果想要对偶问题有意义且和原问题有对应关系（对于 QP 是强对偶关系），那么我们需要满足 KKT 条件，即

\[\begin{aligned} \frac{\partial \mathcal{L}(w, b, \alpha)}{\partial w} &= w - \sum_{i=1}^N \alpha_i y_i x_i = 0 \\ \Rightarrow w & = \sum_{i=1}^N \alpha_i y_i x_i \\ \frac{\partial \mathcal{L}(w, b, \alpha)}{\partial b} &= -\sum_{i=1}^N \alpha_i y_i = 0 \\ 1 - y_i(w^Tx_i + b) &\leq 0 \\ \alpha_i &\geq 0 \\ \alpha_i (1 - y_i(w^Tx_i + b)) &= 0 \end{aligned} \]

此时\(v(D) = v(P)\), 同时\(\alpha^\star\)即对应原问题 KKT 点的乘子。

\(w^\star, b^\star\)可以通过 KKT 求解

\[w^\star = \sum_{i=1}^N \alpha_i^\star y_i x_i \\ \alpha_i^\star (1 - y_i(w^{\star T}x_i + b^\star)) = 0 \]

那么对于\(1 - y_i(w^{\star T}x_i + b^\star) = 0\)的点，我们拥有\(\alpha_i^\star \geq 0\)，我们称之为 支持向量，只要寻找到一个就可以求解\(b^\star\)

\[b^\star = y_i - \sum_{j=1}^N \alpha_j^\star y_j x_j^T x_i \]

然而在实际过程中，为了减少误差，我们可以求解所有支持向量的平均值。

在求解过程中的有趣的现象

1. 目标函数首先我们看对偶问题的目标函数

   \[\max_{\alpha} \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j \\ \text{s.t. } \alpha_i \geq 0, \quad i = 1, 2, \ldots, N \\ \sum_{i=1}^N \alpha_i y_i = 0 \]

   观察\(\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j\)，可以将其写成一个二次型\((\alpha y)^T X^T X (\alpha y)\), 那么如果将\(X\)单位化，\(X^T X\)是一个相似性矩阵（考虑\(cos \theta\)）。不单位化也可以表示相似性。

   那么 SVM 的学习过程可以看作是在一个相似性空间中进行的，类别相同的点在相似性空间中更加接近，而类别不同的点在相似性空间中更加远离。

2. 对偶问题中的约束

   \[\sum_{i=1}^N \alpha_i y_i = 0 \]

   每一个点都有一个乘子，对于不是支持向量的点，\(\alpha_i = 0\)，对于支持向量，\(\alpha_i > 0\)。

   正类与负类的乘子之和为 0，可以看作隐式的对正负类做了平衡性调节。

Soft Margin-SVM

Hard Margin-SVM 考虑的情况非常理想，而对于线性不可分的问题，我们无法求解，因此我们引入了 Soft Margin-SVM。

我们可以引入一个 loss function，对于每一个点，我们引入一个 \(\xi_i\)，\(\xi_i = 0,\quad y_i(wx_i + b) \geq 0\), \(\xi_i = 1-y_i(wx_i + b), \quad y_i(wx_i + b) < 0\), 那么我们可以写出优化目标

\[\min_{w,b,\xi} \frac{1}{2} \| w \|^2 + C \sum_{i=1}^N \xi_i \\ \text{s.t. } y_i(wx_i + b) \geq 1 - \xi_i, \quad i = 1, 2, \ldots, N \\ \xi_i \geq 0, \quad i = 1, 2, \ldots, N \]