crypto--rsa基础（1）

在ctf---crypto中rsa应该是最常见也是现在最容易考到的密码题型吧，这篇博客就简单的介绍一下rsa和rsa的一些基本的攻击手法.
对于我们这些萌新来说要做rsa的话也必须先掌握四大基本公式就是欧拉函数，费马小定理，中国剩余定理，威尔逊定理，现在就先基本了解一下就能够做题了，在网上的百度都能够搜到，这四个定理我就先不解释了。

那么就先简单的介绍一下rsa，网上的rsa都很详细，我这里就简单的介绍一下我自己对于rsa的看法，其中有很多的参数，m：明文，，c：密文，，（d，n):私钥，，（e,n）公钥,，n：模数，，phi:n的欧拉函数，这些就就是rsa一般的参数，但学到后面就会有更多的参数出现，其他的参数就留到之后在解释吧。rsa的加密方式和算法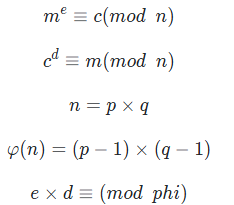就是以上5个式子。可能对于小白来说，不知道mod和同余是什么，简单解释一下，mod就是除一个数取它的余数，第一个式子中的三条横线就是同余的符号，意思就是m^{e和c对n同时取余数相同，也可以写做n|(m}e-c).
那么在以上5个式子中第一个式子就是我们的加密方式，第二个式子就是密文转明文的解密方式。这就是rsa的基本的东西。

这里简单介绍一下几种基本的攻击方式
（1）基本n分解攻击（其中的q和p相差过大或者相差过小），因为n=q*p，如果其中的q和p相差过大或者相差过小都会造成n容易分解。例题：

p=getPrime(512)
q=gmpy2.next_prime(p)#这个式子代表的是求p的下一个素数，那么这样的话就可以直接是使用yafu分解
n=p*q
分解得到了p和q就可以进行简单的攻击了，以下是我们的基本的rsa解密脚本：这是给我们了n和e，c一般步骤就是求出q和p然后求出phi在求出逆元d然后就可以攻击了。

from Crypto.Util.number import *
import gmpy2#这个库是我们做rsa所需要的最基本的库
n=0x80b32f2ce68da974f25310a23144977d76732fa78fa29fdcbf
这边我用yafu分解了n可以得到p和q
p=780900790334269659443297956843
q=1034526559407993507734818408829
e=0x10001
c=0x534280240c65bb1104ce3000bc8181363806e7173418d15762

phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)#这里就是使用求逆元的公式求出d
m=pow(c,d,n)
print（long_to_bytes(m)）

（2）公约数分解n（n不互素）：对于题目中给我们多个n，并且n是不互素的例如：
p1=getPrime(512)
p2=getPrime(512)
q=getPrime(512)
n1=p1q
n2=p2q
俩个n的约数就可以通过gcd求出q，然后进行求解。
例题：[BJDCTF 2020]rsa：

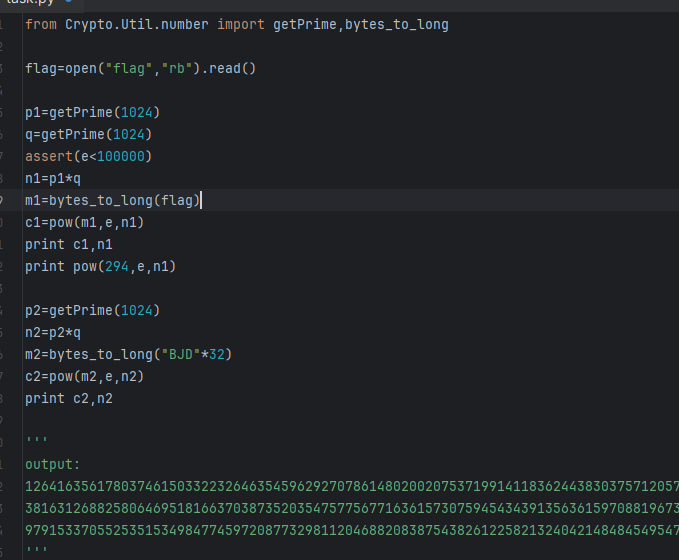
这道题就符合n不互素攻击的条件，但是这道题没有给我们e，给我们了pow（294，e,n1）我们就可以进行爆破得出了e

gcd求出来q然后分别求出来p1和p2（注：这里求出的p2那些都没用，因为我们求得明文是flag，而p2对应得flag是BJD，所以就根本不需要p2，但是其他题就不一样了）

（3）低加密指数攻击：
条件：主要利用的是私钥d很小，表现形式一般是e很大，加密指数指的是e，因为e是可以随机选取的，当e很小时就会被直接破解掉。
当e=3，而且明文也很小，导致明文的三次方仍然小于n，那么通过直接对密文3次开放，即可得到明文。
C=m^emodn
如果e=3，且m^e<n，那么
m^e modn= m^e ，即C=m^e
m=3√c
如果e=3，且m^e>n，那么设k有：
c= m^e +kn
爆破k，如果c−kn能开三次根式，那么可以直接得到明文。
例题：[SWPUCTF 2021 新生赛]crypto5
题目就给我们明文和n，就是低加密指数小明文攻击，因为我们不知道e是多少，我们需要爆破（好烦爆破呀QAQ）

exp：
from Crypto.Util.number import *
import gmpy2
flag = 25166751653530941364839663846806543387720865339263370907985655775152187319464715737116599171477207047430065345882626259880756839094179627032623895330242655333
e = 2
e从2开始遍历，随便找一个较小的值，我这里取的是26。运行找到可以开e次方的flag，并得到其结果
while(e < 26):
e += 1
print(gmpy2.iroot(flag , e))# gmpy2.iroot是让flag开e次方

(4)低加密指数广播攻击：RSA低加密指数广播攻击
首先介绍什么是广播，加入我们需要将一份明文进行多份加密，但是每份使用不同的密钥，密钥中的模数n不同但指数e相同且很小，我们只要拿到多份密文和对应的n就可以利用中国剩余定理进行解密。
使用条件：
加密指数e非常小
一份明文使用不同的模数n，相同的加密指数e进行多次加密
可以拿到每一份加密后的密文和对应的模数n、加密指数e

基本得脚本：
e =
n=[]
def op(x):
res = 1
for i in x:
res *= i
return res
def CRT(m, a):
assert (len(m) == len(a))
M = op(m)
sum = 0
for m, a in zip(m, a):
Mi = M // m
ti = invert(Mi, m)
sum += a * ti * Mi
return sum % M
m = CRT(n, c)
m1 = iroot(m, e) # 开e次方，这个是求一个m1的e次方小于m
print(m1)
print(libnum.n2s(int(m1[0])))#这个是小于m的最大的那个数所以是0那个位置
这里需要中国剩余定理，这里对于萌新知道怎么使用就行了，到时候熟悉了中国剩余定理（CRT）就可以自己取推导了。

（5):共模攻击：使用得条件：若干次加密，e不同，n相同，m相同。就可以在不分解n和求d的前提下，解出明文m。
推导得过程首先，两个加密指数互质：
gcd(e1,e2)=1
即存在s1、s2使得：
s1+e1+s2e2=1
又因为：
c1≡m^e1 mod n
c2≡m mod n
代入化简可得：
c1^s1 * c2^s2 ≡ m mod n

即可求出明文，基本脚本如下
import libnum
import gmpy2
n=103606706829811720151309965777670519601112877713318435398103278099344725459597221064867089950867125892545997503531556048610968847926307322033117328614701432100084574953706259773711412853364463950703468142791390129671097834871371125741564434710151190962389213898270025272913761067078391308880995594218009110313
e1=3247473589
e2=3698409173
c1=100156221476910922393504870369139942732039899485715044553913743347065883159136513788649486841774544271396690778274591792200052614669235485675534653358596366535073802301361391007325520975043321423979924560272762579823233787671688669418622502663507796640233829689484044539829008058686075845762979657345727814280
c2=86203582128388484129915298832227259690596162850520078142152482846864345432564143608324463705492416009896246993950991615005717737886323630334871790740288140033046061512799892371429864110237909925611745163785768204802056985016447086450491884472899152778839120484475953828199840871689380584162839244393022471075

def exp_def(e1,e2,c1,c2,n):
s,s1,s2 = gmpy2.gcdext(e1, e2)
m = (pow(c1,s1,n) * pow(c2 ,s2 ,n)) % n 这里就是求解出来得公式
return int(m)
m=exp_def(e1,e2,c1,c2,n)
print(libnum.n2s(m))
其实本人学习rsa也没有多久，还得加以勉励自己学习，坚持就是胜利！