数据结构—树表的查找-编程知识

数据结构—树表的查找

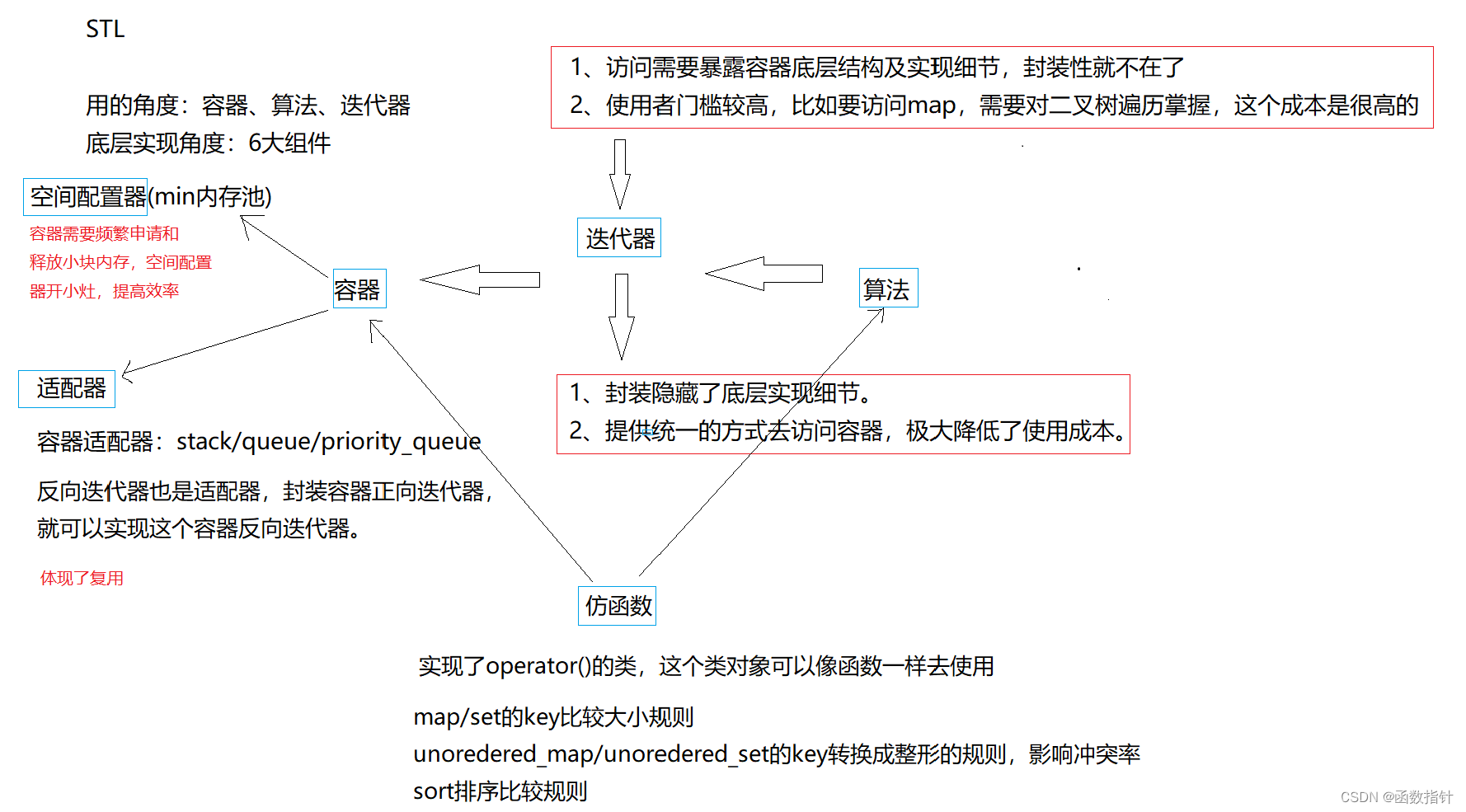
7.3树表的查找

当表插入、删除操作频繁时，为维护表的有序表，需要移动表中很多记录。

改用动态查找表——几种特殊的树

表结构在查找过程中动态生成

对于给定值key

若表中存在，则成功返回；

否则，插入关键字等于key的记录

7.3.1二叉排序树

二叉排序树（Binary Sort Tree）又称为二叉搜索树、二叉查找树。

定义：

二叉排序树或是空树，或是满足如下性质的二叉树：(1)若其左子树非空，则左子树上所有结点的值均小于根结点的值；(2)若其右子树非空，则右子树上所有结点的值均大于等于根结点的值；(3)其左右子树本身又各是一棵二叉树

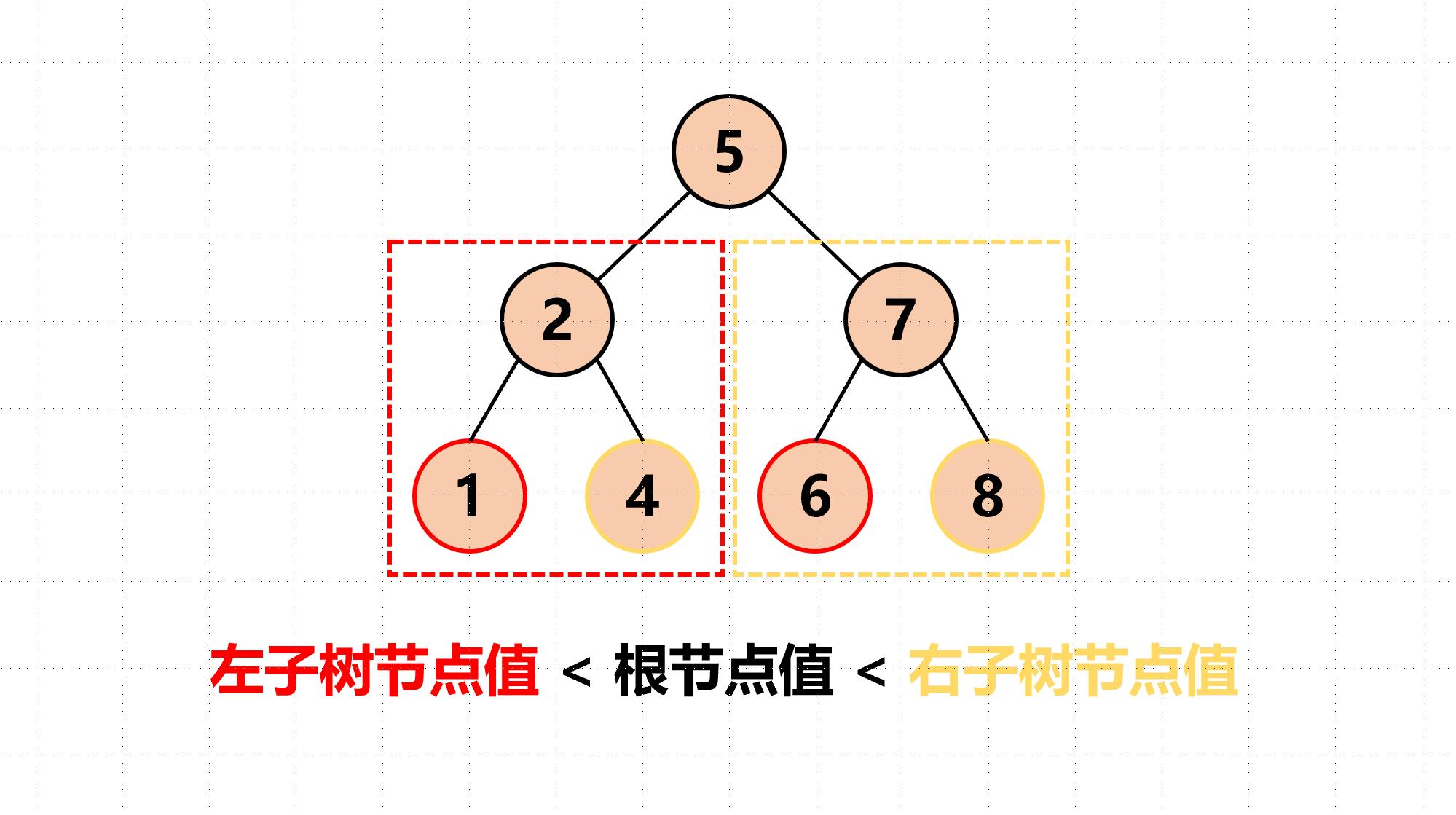
#图解数据结构：二叉排序树 - 知乎

二叉排序树的性质：

中序遍历非空的二叉排序树所得的数据元素序列时一个按关键字排序的递增有序序列。

二叉排序树的存储结构

typedef struct{KeyType key;//关键字项InfoType otherinfo;//其他数据域
}ElemType;

typedef struct BSTNode{ElemType data;//数据域struct BSTNode *lchild,*rchild;//左右孩子指针
}BSTree T;
BSTree T；//定义二叉排序树

查找

若查找的关键字等于根结点，成功
否则
- 若小于根结点，查其左子树
- 若大于根结点，查其右子树
在左右子树上的操作类似

1、二叉排序树的递归查找

【算法思想】

若二叉排序树为空，则查找失败，返回空指针。
若二叉排序树非空，将给定值key与根结点的关键字T->data.key进行比较：
- 若key等于T->data.key，则查找成功，返回根结点地址；
- 若key小于T->data.key，则进一步查找左子树；
- 若key大于T->data.key，则进一步查找左子树。

BSTree SerachBT(BSTree T,KeyType key){if((!T)||key==T->data.key) return T;else if(key<T->data.key)return SearchBST(T->lchild,key);//在左子树中继续查找else return SearchBST(T->rchild,key);//在右子树中继续查找
}

二叉排序树的查找分析

二叉排序树上查找某关键字等于给定值的结点过程，其实就是走了一条从根到该结点的路径。

比较的关键字次数=此结点所在层次数

最多的比较次数=数的深度

问题：如何提高形态不均衡的二叉排序树的查找效率？

解决办法：做“平衡化”处理，即尽量让二叉树的形状均衡！

2、二叉排序树的插入

若二叉排序树为空，则插入结点作为根结点插入到空树中
否则，继续在其左、右子树上查找
- 树中已有，不再插入
- 树中没有
  - 查找直至某个叶子结点的左子树或右子树为空为止，则插入结点应为该叶子结点的左孩子或右孩子。

插入的元素一定在叶节点上

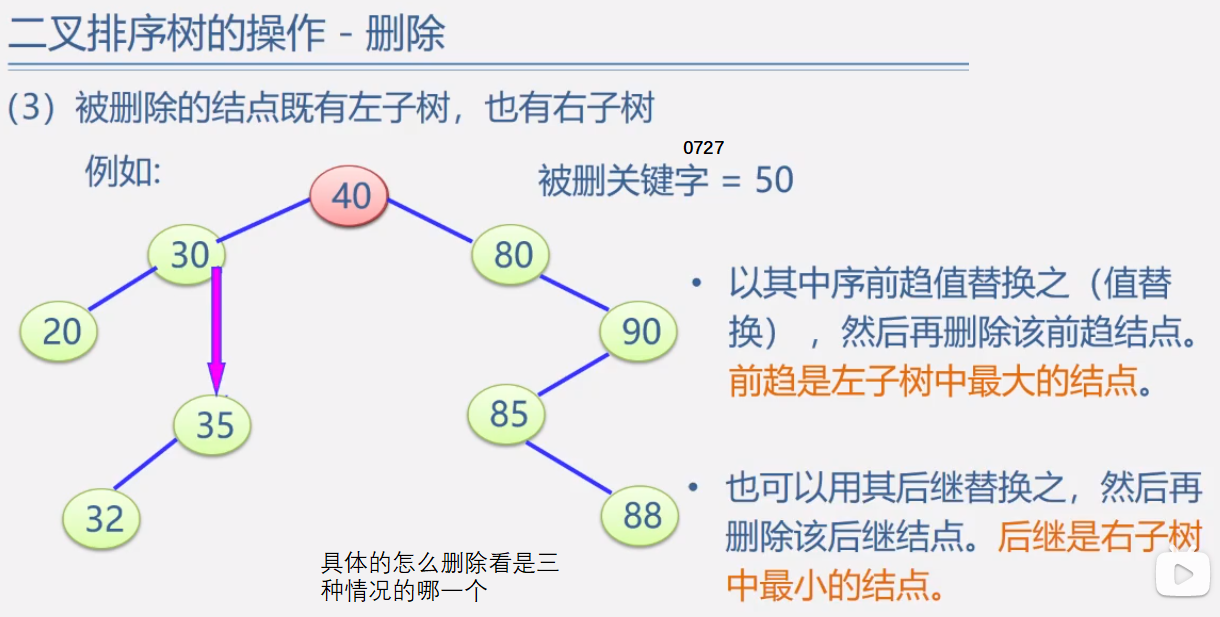
3、二叉排序树的删除

从二叉排序树中删除一个结点，不能把以该结点为根的子树都删去，只能删掉该结点，并且还应保证删除后所得的二叉树仍然满足二叉排序树的性质不变。

由于中序遍历二叉排序树可以得到一个递增有序的序列。那么，在二叉排序树删去一个结点相当于删去有序序列中的一个结点。

将因删除结点而断开的二叉链表重新链接起来
防止重新链接后树的高度增加

数据结构（34）二叉排序树__李白_的博客-CSDN博客_数据结构中什么是二叉排序树

4、二叉排序树的生成

从空树出发，经过一系列的查找、插入操作之后，可生成一棵二叉排序树。

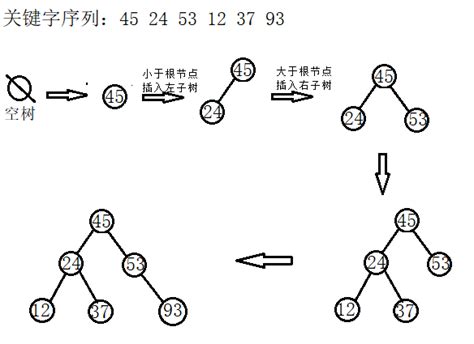
数据结构之二叉排序树（C语言实现）_kang___xi的博客-CSDN博客_二叉排序树的实现

一个无序序列可通过构造二叉排序树而变成一个有序序列。构造树的过程就是对无序序列进行排序的过程。

插入的结点均为叶子结点，故无序移动其他结点。相当于在有序序列上插入记录而无需移动其他记录。

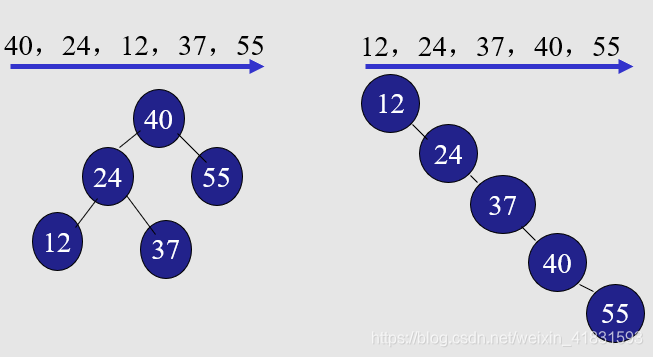
关键字的输入顺序不同，建立的二叉排序树不同

7.3.2平衡二叉树

1.平衡二叉树的定义

平衡二叉树（balance binary tree）

又称AVL树
一棵平衡二叉树或者是空树，或者是具有下列性质的二叉排序树：
- 左子树与右子树的高度之差的绝对值小于等于1；
- 左子树和右子树也是平衡二叉排序树。
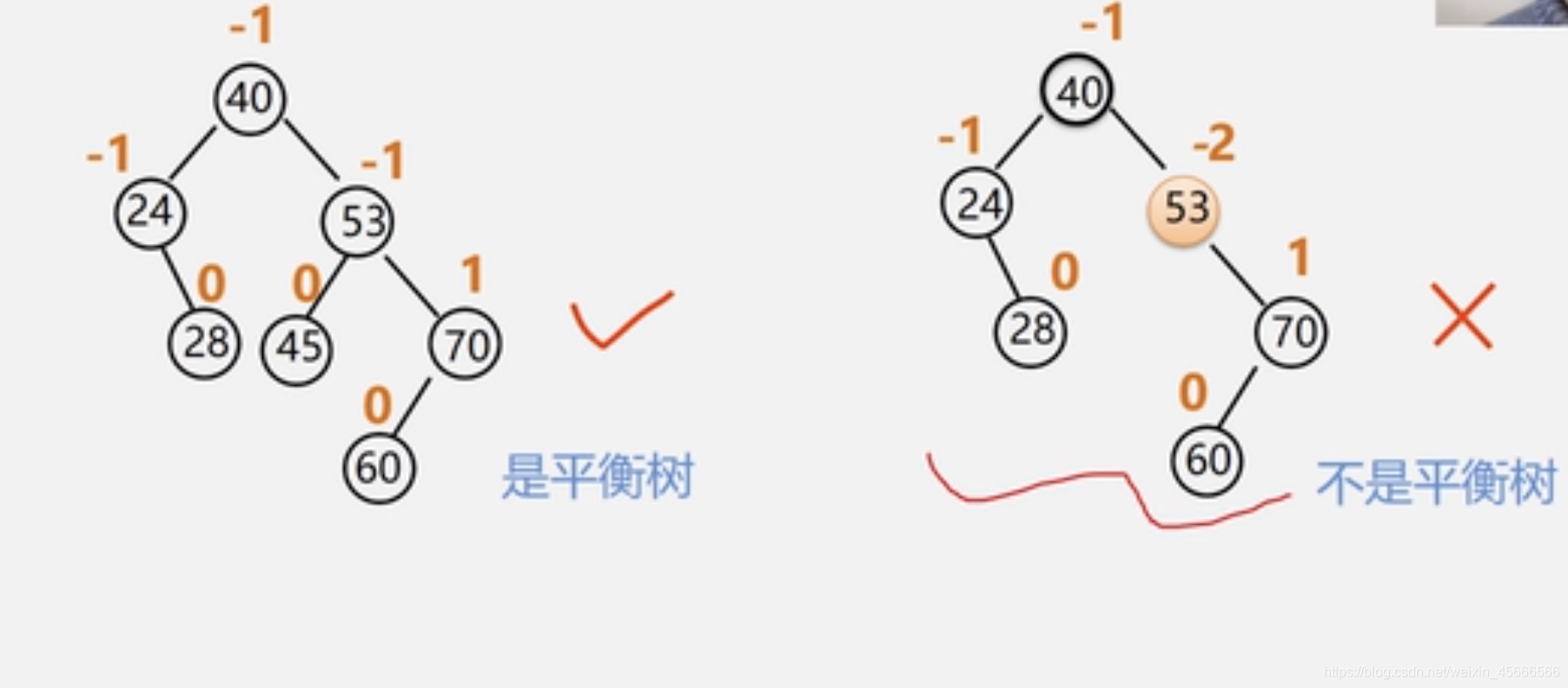
为了方便起见，给每个结点附加一个数字，给出该结点左子树与右子树的高度差。这个数字称为结点的平衡因子（BF）。

平衡因子 = 结点左子树的高度 - 结点右子树的高度

根据平衡二叉树的定义，平衡二叉树上所有结点的平衡因子只能是-1、0或1。