智能计算系统-Tensorflow框架的计算图机制
陈云霁老师的课,趁现在有时间,打算了解深度学习的底层原理。
从第五章编程框架机理开始,一到四章是深度学习基础,在此不再讨论
一. 深度学习框架的设计原则
1. 高性能
主要体现在
- 神经网络的算子,针对底层硬件进行充分优化
- 在计算图上进行一系列优化
- 根据网络结构,并发的计算没有数据依赖的节点
2. 易开发
共性运算封装为算子
3. 可移植
针对每个算子,提供不同设备的不同底层实现
二. Tensorflow的计算图原则
1. 计算图的自动求导机制
基于计算图实现自动求导方法。
求导共有四种方法:
-
手动求导法:人工求,最为麻烦,在此略过
-
数值求导法:
依赖导数的定义:
\[f(x) = \lim_{h→0} \frac{f(x+h)-f(x)}{h} \]相当于直接根据导数定义,在输入中添加改动h,再算一次结果,最终相减并作除法得到导数
这种方法简单直观,可对用户隐藏求导过程
但是,计算量大,极易引起舍入、截断误差(如计算sin等)
-
符号求导法:利用求导规则对表达式操作,最后代入数值,从而获得导数
如下图所示:

这种方法在反向传播后导数的表达式会过于庞大
-
自动求导法:这是介于数值求导和符号求导之间的方法。
核心为算子内用符号求导,算子之间按照计算图拓扑顺序从后向前带入数值
举个例子理解:
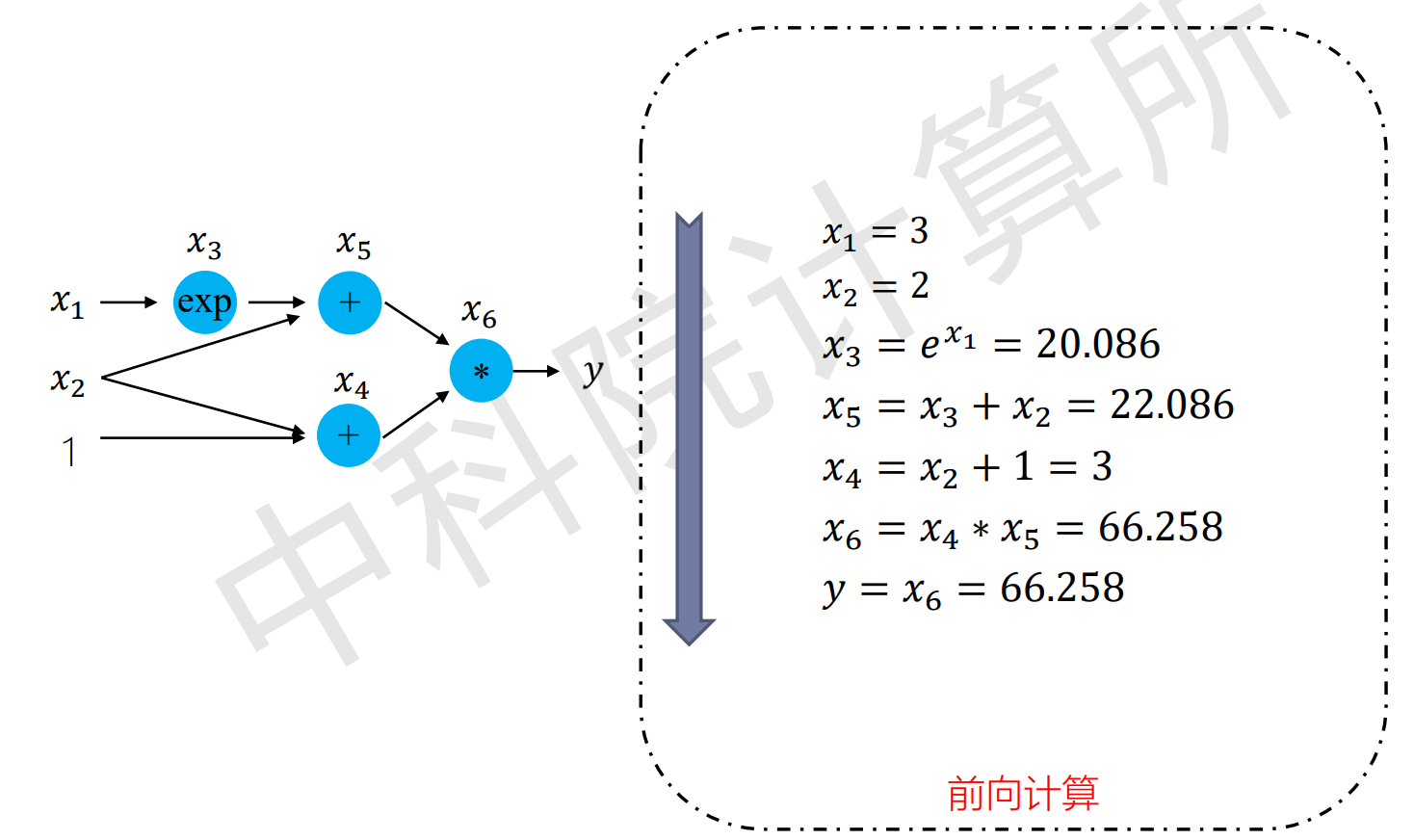
上面这幅图是tensorflow的计算图示例,也展现了前向传播的过程。
当反向计算各个节点的梯度时,结果如下:
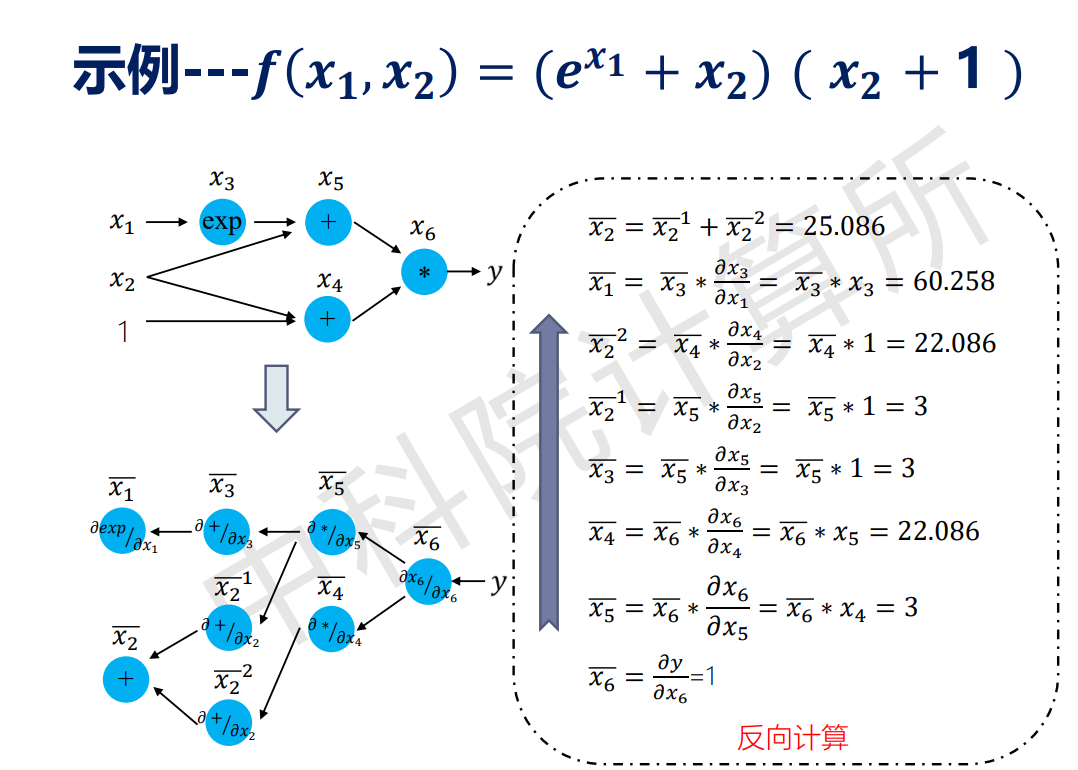
从图里面可以发现:
先用符号求导得到每个算子的导数表达式,
之后从后往前,反向带入数值。
这样的自动求导机制,十分适合计算图机制
四种方法的对比效果如下:
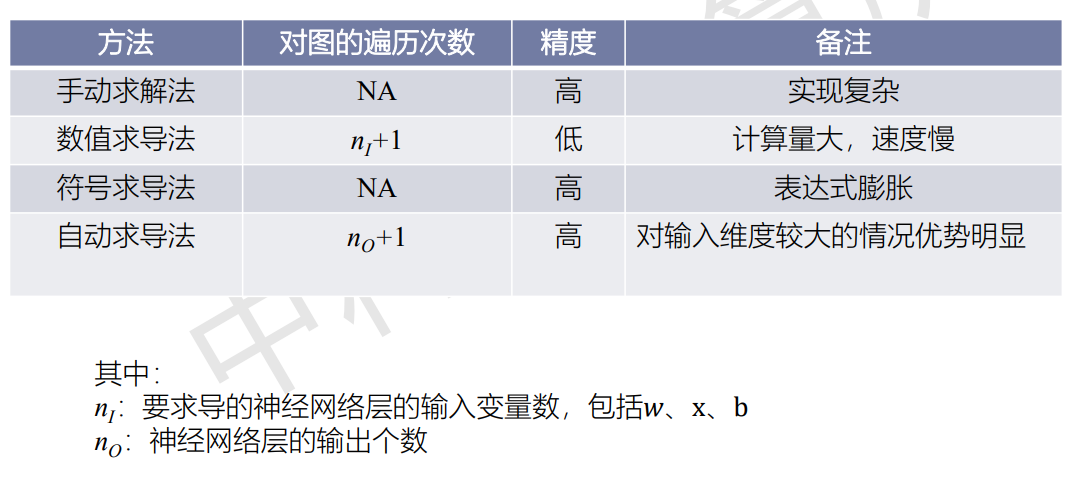
2. 检查点机制
实例化saver对象,以及实现神经网络中所有变量的保存与回复。
saver = tf.train.Saver()
saver.save(sess, "./ckpt/my-model")
saver.restore(sess, ckpt)