大家好,我是Weekoder!
今天的内容是快速幂!(实际上是为了讲矩阵快速幂赶出来的嘻嘻
快速幂,顾名思义就是快速地计算出某个数的幂,形如 \(a^n\)。
为什么普通的幂运算慢?假设要计算 \(a^n\),则需要拆分成 \(a\times a\times\cdots\times a\times a\),运算 \(n\) 次,复杂度为 \(O(n)\)。当 \(n\) 很大时,这个算法明显就不行了。那要怎么优化呢?我们先来看一个简单一点的例子:当 \(n\) 为 \(2\) 的幂时,可以怎么做呢?假设 \(n\) 为 \(32\),可以这样计算:
注意:\(a^x\times a^y=a^{x+y}\)。
可以发现,这样只计算了 \(5\) 次,相比于朴素算法的 \(32\) 次,将时间复杂度优化到了 \(O(\log n)\)。这其实是倍增的原理,相比于一个一个乘 \(a\),不如将 \(a\) 的数量翻倍乘。
那如果 \(n\) 不是 \(2\) 的幂呢?比如,\(n=105\) 的时候,该怎么办呢?虽然 \(105\) 不是 \(2\) 的幂,但是我们发现 \(105\) 可以拆分成 \(2\) 的幂之和,像这样:
于是,我们可以把 \(a^{105}\) 拆分一下:
我们在刚刚提到过,计算 \(n\) 是 \(2\) 的幂的情况是很容易的,所以我们只需要将它们相乘即可。
这个问题的关键在于,怎样将一个数拆分成 \(2\) 的幂之和?我们来看一下他们在二进制下的样子:
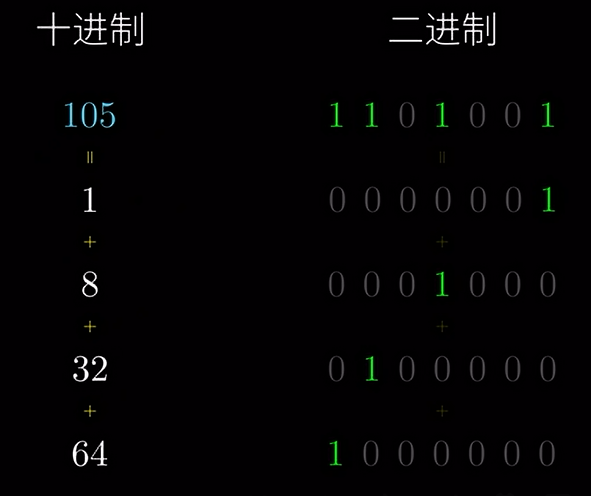
可以看到,\(105\) 的二进制中有 \(4\) 个 \(1\),而 \(2\) 的幂的数都只有一个 \(1\),并且刚好和 \(105\) 的四个 \(1\) 位置一样。所以,只要将 \(105\) 二进制中的 \(1\) 拆开,就能得到 \(2\) 的幂的数字是哪些了。
而因为一个数 \(n\) 的二进制最多只有 \(\log n\) 位,所以时间复杂度为 \(O(\log n)\)。
就决定是你了!快速幂模板!
先上代码:
#include <bits/stdc++.h>
using namespace std;typedef long long ll;ll expow(ll a, ll n, ll p) {ll r = 1;while (n) {if (n & 1) r = r * a % p;a = a * a % p, n >>= 1;}return r;
}int main() {ll a, b, p;cin >> a >> b >> p;cout << a << "^" << b << " mod " << p << "=" << expow(a, b, p);return 0;
}
输入和输出就不用我讲了,重点是 \(\text{expow}\) 函数。我把快速幂函数提取出来(先不取模):
typedef long long ll;ll expow(ll a, ll n) {ll r = 1;while (n) {if (n & 1) r *= a;a *= a, n >>= 1;}return r;
}
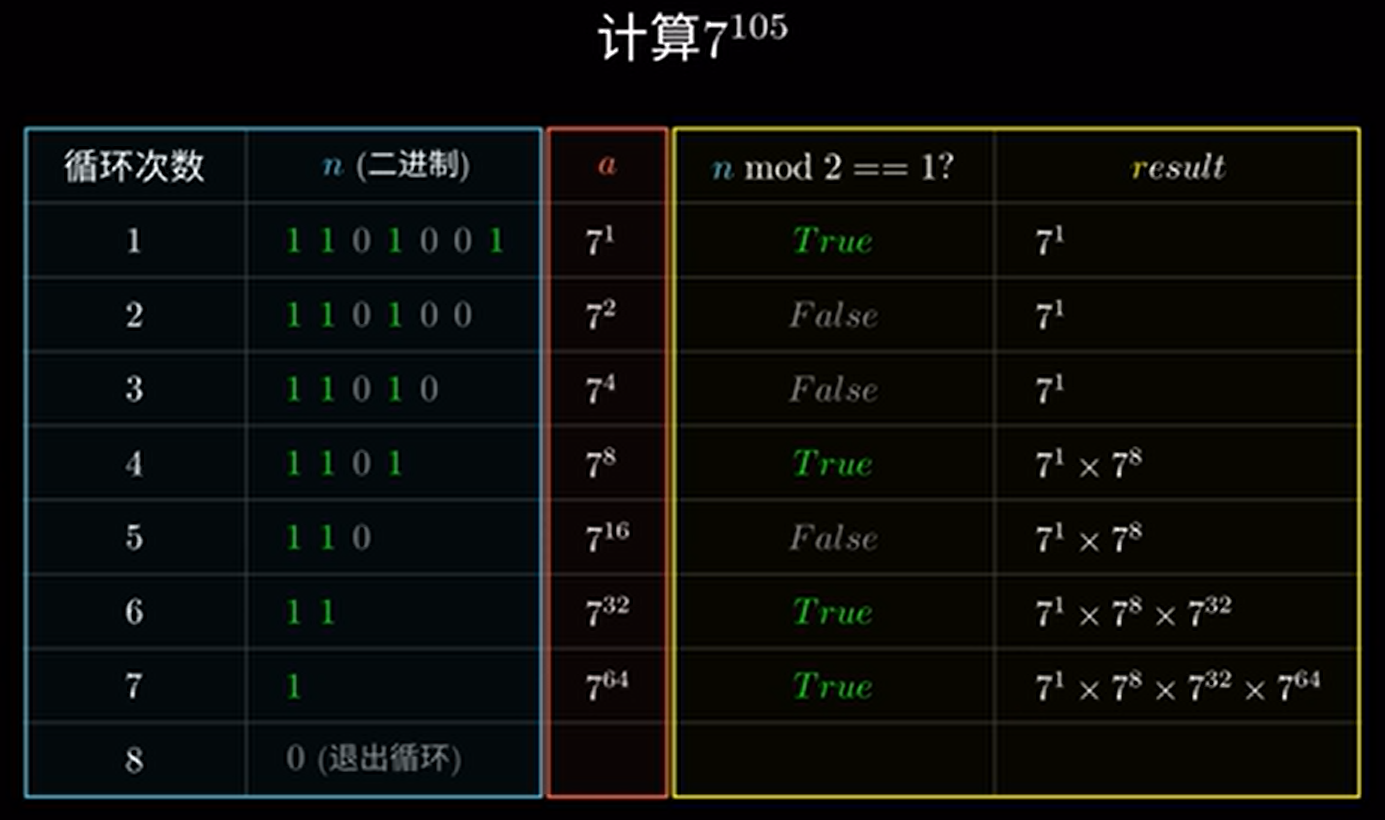
比如计算 \(7^{105}\)。
首先,我们用一个 \(\color{yellow}\texttt{r}\color{#000000}\texttt{esult}\) 来存储结果,初始时为 \(1\)。接着,有一个 \(\text{while}\) 循环,其实就是遍历 \(n\) 在二进制下的每一位。如果当前这一位是 \(1\),即 \(n\) 对 \(1\) 按位与的结果为 \(1\),则可以拆分,将 \(r\) 乘上 \(a\)。每过一位,\(a\) 就变为 \(a^2\),即模拟倍增的过程。然后还要将 \(n\) 除以 \(2\),用位运算表示就是右移一位,获取下一位。最后返回结果 \(r\)。可以辅助图片理解。
这样就可以用 \(O(\log n)\) 的速度计算 \(a^n\) 了。
小扩展:幂取模
即计算 \(a^n \bmod p\)。
只需要在快速幂的模板里稍微改动一下。在做乘法运算时,顺带取模就行了。
幂取模模板代码如下:
typedef long long ll;ll expow(ll a, ll n, ll p) {ll r = 1;while (n) {if (n & 1) r = r * a % p;a = a * a % p, n >>= 1;}return r;
}
综上所述,二进制快速幂的核心就是这些了。当然,快速幂除了计算 \(a^n\) 以外,还有很多用处等着你去发现。