运筹学练习Python精解——图与网络

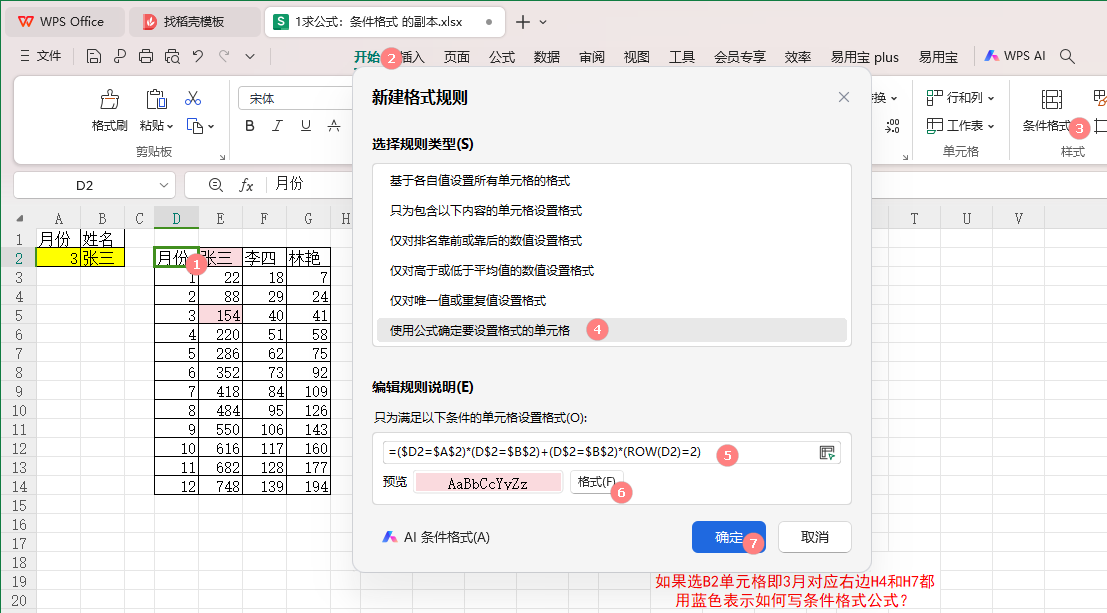
练习1

北京(Pe)、东京(T)、纽约(N)、墨西哥(M)、伦敦(L)、巴黎(Pa)各城市之间的航线距离如下表所示。从北京（Pe）乘飞机到东京(T)、纽约(N)、墨西哥城(M)、伦敦(L)、巴黎(Pa)五城市做旅游，每城市恰去一次再返回北京，应如何安排旅游线，使旅程最短？

	L	M	N	Pa	Pe	T
L	0	56	35	21	51	60
M	56	0	21	57	78	70
N	35	21	0	36	68	68
Pa	21	57	36	0	51	61
Pe	51	78	68	51	0	13
T	60	70	68	61	13	0

解决这个问题需要使用旅行商问题（TSP）的经典算法之一。我们可以使用蛮力法来求解，因为这是一个小规模的问题，有6个城市。这种方法将考虑所有可能的路线并找到总距离最短的那个。可以使用Python编写代码来实现这个功能。

from itertools import permutations# 城市的索引
cities = ["L", "M", "N", "Pa", "T"]# 城市间的距离矩阵
dist_matrix = [[0, 56, 35, 21, 60],  # L[56, 0, 21, 57, 70],  # M[35, 21, 0, 36, 68],  # N[21, 57, 36, 0, 61],  # Pa[60, 70, 68, 61, 0],  # T
]# 北京到其他城市的距离
beijing_distances = [51, 78, 68, 51, 13]# 将城市名称映射到索引
city_indices = {city: i for i, city in enumerate(cities)}# 获取所有城市的排列
city_permutations = permutations(cities)# 定义一个函数计算一个路线的总距离
def total_distance(route):total_dist = beijing_distances[city_indices[route[0]]]  # 从北京到第一个城市的距离n = len(route)for i in range(n - 1):total_dist += dist_matrix[city_indices[route[i]]][city_indices[route[i + 1]]]total_dist += beijing_distances[city_indices[route[-1]]]  # 最后一个城市返回北京的距离return total_dist# 变量初始化
min_distance = float('inf')
best_route = None# 遍历所有可能的城市排列
for perm in city_permutations:dist = total_distance(perm)if dist < min_distance:min_distance = distbest_route = perm# 输出最优路径和最短距离
print("最优路径: Pe ->", " -> ".join(best_route), "-> Pe")
print("最短距离:", min_distance)

最优路径: Pe -> Pa -> L -> N -> M -> T -> Pe
最短距离: 211

练习2

原图	网络图	最小树

import heapq
import networkx as nx
import matplotlib.pyplot as plt# 定义图的邻接矩阵
graph = {'v0': {'v1': 2, 'v2': 1, 'v3': 3, 'v4': 4, 'v5': 4, 'v6': 2, 'v7': 5, 'v8': 4},'v1': {'v0': 2, 'v2': 4, 'v8': 1},'v2': {'v0': 1, 'v1': 4, 'v3': 1},'v3': {'v0': 3, 'v2': 1, 'v4': 1},'v4': {'v0': 4, 'v3': 1, 'v5': 5},'v5': {'v0': 4, 'v4': 5, 'v6': 2},'v6': {'v0': 2, 'v5': 2, 'v7': 3},'v7': {'v0': 5, 'v6': 3, 'v8': 5},'v8': {'v0': 4, 'v1': 1, 'v7': 5}
}# 使用Prim算法计算最小生成树
def prim(graph, start):min_heap = [(0, start, None)]mst_edges = []total_cost = 0visited = set()while min_heap:cost, node, parent = heapq.heappop(min_heap)if node in visited:continuevisited.add(node)if parent is not None:mst_edges.append((parent, node, cost))total_cost += costfor neighbor, weight in graph[node].items():if neighbor not in visited:heapq.heappush(min_heap, (weight, neighbor, node))return mst_edges, total_cost# 计算最小生成树
mst_edges, total_cost = prim(graph, 'v0')# 打印最小生成树的边和总权重
print("最小生成树的边:")
for edge in mst_edges:print(edge)
print("最小生成树的总权重:", total_cost)# 创建NetworkX图
G = nx.Graph()# 添加节点和边
for node, edges in graph.items():for neighbor, weight in edges.items():G.add_edge(node, neighbor, weight=weight)# 使用相同的布局绘制原图和最小生成树图
pos = nx.spring_layout(G)plt.figure(figsize=(8, 8))# 绘制原图
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=1000, font_size=20)  # 放大节点和字体
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels, font_size=20)  # 放大权重标签# 绘制最小生成树的边
mst_edges_set = set((u, v) for u, v, _ in mst_edges)
mst_labels = {edge: G.edges[edge]['weight'] for edge in mst_edges_set}
nx.draw_networkx_edges(G, pos, edgelist=mst_edges_set, edge_color='blue', width=4)  # 放大最小生成树的边
nx.draw_networkx_edge_labels(G, pos, edge_labels=mst_labels, font_color='blue', font_size=20)  # 放大最小生成树的权重标签plt.title('Graph with Minimum Spanning Tree', fontsize=20)  # 放大标题字体
plt.show()