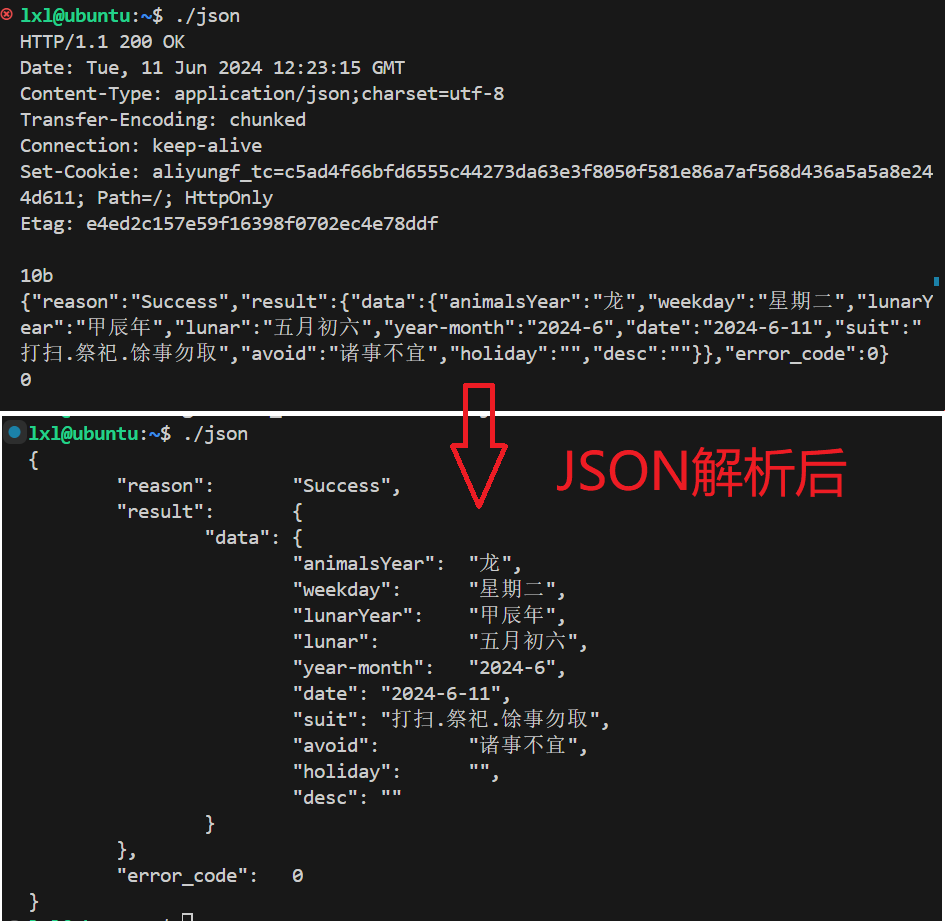
模板题,但码量大。本题主要考察的是存图的方式。
图的类别
有向图:简单来说是指一副具有方向性的图。例如节点 \(a\) 指向节点 \(b\) ,则只能从 \(a\) 走到 \(b\),而不能从 \(b\) 走到 \(a\)。
无向图:若一个图中每条边都是无方向的,则称为无向图。如果一个图为无向图,则既可以从节点 \(a\) 走到节点 \(b\),又可以从 \(b\) 走到 \(a\)。
赋权图:若一个图中连接两个节点的边有长度,则这个图是赋权图。
图的存储方式
邻接矩阵
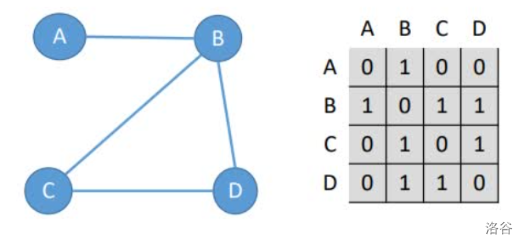
邻接矩阵是一个 \(n\) 行 \(n\) 列的矩阵,\(n\) 代表节点数。仅能在一张无重边的图中使用。
赋权图
假如节点 \(i\) 连接节点 \(j\),则将矩阵中第 \(i\) 行第 \(j\) 列设为边权,表示这里有一条长度为 \(w\) 的边。
无权图
存法都差不多只不过将第 \(i\) 行第 \(j\) 列的值设为一。仅表示这里有一条边。
注意
邻接矩阵中如果节点 \(a\) 连接节点 \(b\) 且这个图为无向图,那么第 \(a\) 行第 \(b\) 列和第 \(b\) 行第 \(a\) 列都要赋值,因为两边都可以走。如下图。
代码实现
jz[u][v]=w //节点u到节点v之间有一条长为w的边
关联矩阵
同样是一个二维数组,他记录的是一个点与一条边的关系。并且关联矩阵仅能在一张无自环并且无权的图中使用。
存法
现在第 \(i\) 条边上有节点 \(u\) 和 \(v\) 相连,如果点 \(u\) 在第 \(i\) 条边中作为起点出现,则将 \(b_{u,i}=1\),否则等于负一。 如果这个图是无向图则将 \(b_{u,i}\) 和 \(b_{v,i}\) 都设为一。如下。

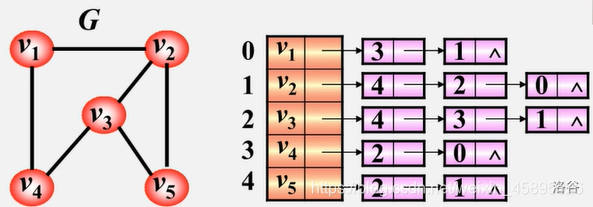
邻接链表
相对于邻接矩阵,邻接表虽然更加复杂却极大减少了空间复杂度。邻接表就相当于一维数组与链表的结合体。同时他还有一个熟悉的名字,链式前向星
存法
顶点: 按编号顺序将顶点数据存储在一维数组中。
关联同一顶点的边: 用线性链表存储。
无向图
有向图
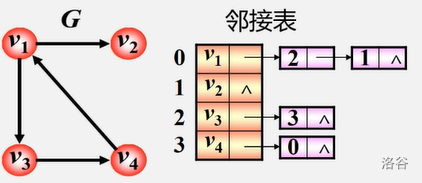
链式前向星
void add(int x,int y,int v){ //x节点指向y节点,长度为vc[++cnt].v=v;c[cnt].to=y;c[cnt].next=h[x];h[x]=cnt;
}
正向表/逆向表
正向表
当对图 \(G\) 的节点与边进行编号后,正向表将每个节点
的直接后继集中在一起存放。
有向图的正向表有一个 \((n+1)\) 维向量 \(A\),一个 \(m\) 维向量 \(B\) 组成。
\(A(i)\) 表示节点 \(v_i\) 的第一个后继在 \(B\) 中的地址。\(B\) 中存放这些后继节点的编号,即 \(A(n+1)=m+1\)。
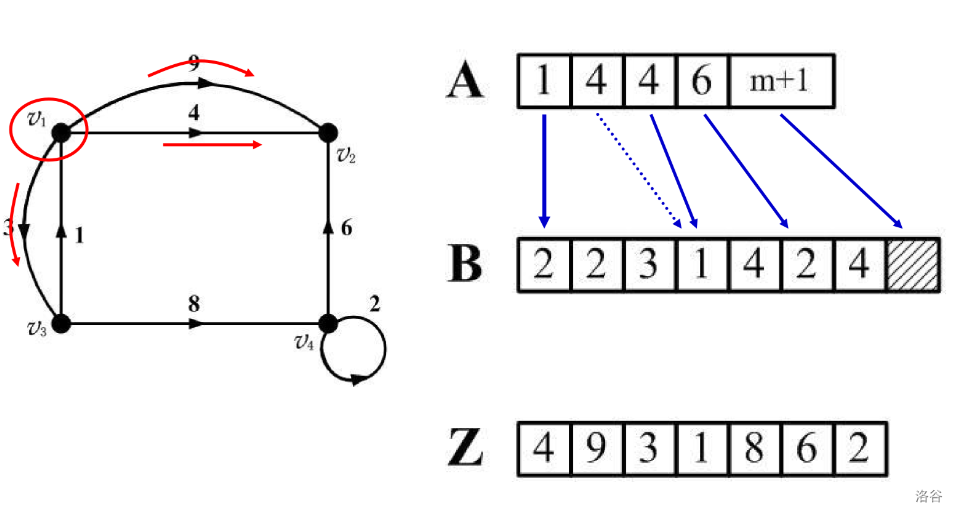
逆向表
与正向表相反,逆向表是将每个结点的直接前驱 集中在一起存放