过去虽然没有细看,但印象里一直觉得变分自编码器(Variational Auto-Encoder,VAE)是个好东西。于是趁着最近看概率图模型的三分钟热度,我决定也争取把VAE搞懂。于是乎照样翻了网上很多资料,无一例外发现都很含糊,主要的感觉是公式写了一大通,还是迷迷糊糊的,最后好不容易觉得看懂了,再去看看实现的代码,又感觉实现代码跟理论完全不是一回事啊。
终于,东拼西凑再加上我这段时间对概率模型的一些积累,并反复对比原论文《Auto-Encoding Variational Bayes》,最后我觉得我应该是想明白了。其实真正的VAE,跟很多教程说的的还真不大一样,很多教程写了一大通,都没有把模型的要点写出来~于是写了这篇东西,希望通过下面的文字,能把VAE初步讲清楚。
分布变换 #
通常我们会拿VAE跟GAN比较,的确,它们两个的目标基本是一致的——希望构建一个从隐变量Z𝑍生成目标数据X𝑋的模型,但是实现上有所不同。更准确地讲,它们是假设了Z𝑍服从某些常见的分布(比如正态分布或均匀分布),然后希望训练一个模型X=g(Z)𝑋=𝑔(𝑍),这个模型能够将原来的概率分布映射到训练集的概率分布,也就是说,它们的目的都是进行分布之间的变换。
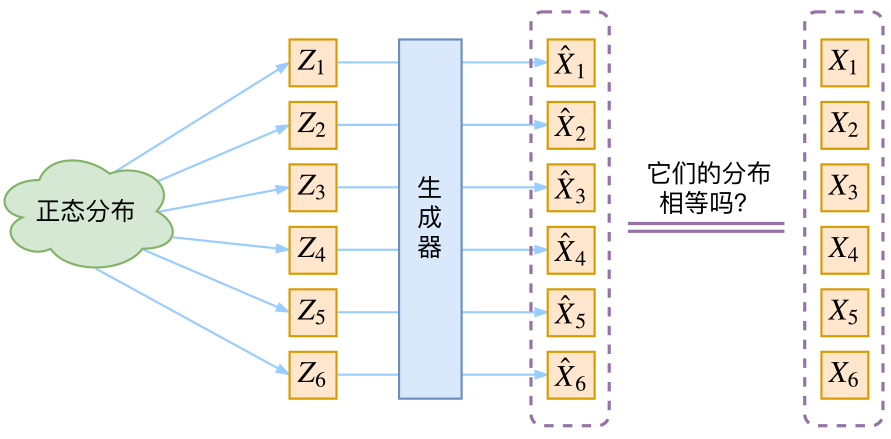
生成模型的难题就是判断生成分布与真实分布的相似度,因为我们只知道两者的采样结果,不知道它们的分布表达式
那现在假设Z𝑍服从标准的正态分布,那么我就可以从中采样得到若干个Z1,Z2,…,Zn𝑍1,𝑍2,…,𝑍𝑛,然后对它做变换得到X^1=g(Z1),X^2=g(Z2),…,X^n=g(Zn)𝑋^1=𝑔(𝑍1),𝑋^2=𝑔(𝑍2),…,𝑋^𝑛=𝑔(𝑍𝑛),我们怎么判断这个通过g𝑔构造出来的数据集,它的分布跟我们目标的数据集分布是不是一样的呢?有读者说不是有KL散度吗?当然不行,因为KL散度是根据两个概率分布的表达式来算它们的相似度的,然而目前我们并不知道它们的概率分布的表达式,我们只有一批从构造的分布采样而来的数据{X^1,X^2,…,X^n}{𝑋^1,𝑋^2,…,𝑋^𝑛},还有一批从真实的分布采样而来的数据{X1,X2,…,Xn}{𝑋1,𝑋2,…,𝑋𝑛}(也就是我们希望生成的训练集)。我们只有样本本身,没有分布表达式,当然也就没有方法算KL散度。
虽然遇到困难,但还是要想办法解决的。GAN的思路很直接粗犷:既然没有合适的度量,那我干脆把这个度量也用神经网络训练出来吧。就这样,WGAN就诞生了,详细过程请参考《互怼的艺术:从零直达WGAN-GP》。而VAE则使用了一个精致迂回的技巧。