ok兄弟们,今天本蒟蒻来做一篇小小的题解
Equalize
题面翻译
有一个给定的长度为 $n$ 的数列 $a$,现在加上一个排列 $b$,即 $c_i=a_i+b_i$。
现在求对于所有可能的 $b$,$c$ 中出现最多的数的出现次数的最大值。
translate by @UniGravity.
题目描述
Vasya has two hobbies — adding permutations $ ^{\dagger} $ to arrays and finding the most frequently occurring element. Recently, he found an array $ a $ and decided to find out the maximum number of elements equal to the same number in the array $ a $ that he can obtain after adding some permutation to the array $ a $ .
More formally, Vasya must choose exactly one permutation $ p_1, p_2, p_3, \ldots, p_n $ of length $ n $ , and then change the elements of the array $ a $ according to the rule $ a_i := a_i + p_i $ . After that, Vasya counts how many times each number occurs in the array $ a $ and takes the maximum of these values. You need to determine the maximum value he can obtain.
$ ^{\dagger} $ A permutation of length $ n $ is an array consisting of $ n $ distinct integers from $ 1 $ to $ n $ in arbitrary order. For example, $ [2,3,1,5,4] $ is a permutation, but $ [1,2,2] $ is not a permutation ( $ 2 $ appears twice in the array), and $ [1,3,4] $ is also not a permutation ( $ n=3 $ but there is $ 4 $ in the array).
输入格式
Each test consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1 \leq t \leq 2 \cdot 10^4 $ ) — the number of test cases. Then follows the description of the test cases.
The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — the length of the array $ a $ .
The second line of each test case contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \le a_i \le 10^9 $ ) — the elements of the array $ a $ .
It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .
输出格式
For each test case, output a single number — the maximum number of elements equal to the same number after the operation of adding a permutation.
样例 #1
样例输入 #1
7
2
1 2
4
7 1 4 1
3
103 102 104
5
1 101 1 100 1
5
1 10 100 1000 1
2
3 1
3
1000000000 999999997 999999999
样例输出 #1
2
2
3
2
1
1
2
提示
In the first test case, it is optimal to choose $ p = [2, 1] $ . Then after applying the operation, the array $ a $ will be $ [3, 3] $ , in which the number $ 3 $ occurs twice, so the answer is $ 2 $ .
In the second test case, one of the optimal options is $ p = [2, 3, 1, 4] $ . After applying the operation, the array $ a $ will be $ [9, 4, 5, 5] $ . Since the number $ 5 $ occurs twice, the answer is $ 2 $ .
本题需要我们做的就是,在题目给的A数组的基础上,对其添加一个序列。
(序列中每个数字只能添加一次)
本题的关键就是要理解如何添加序列以及序列的关键节点。
那么该如何添加序列呢?首先,请各位思考一下,1和1可能在添加该序列后出现相同的值吗?因为同一个值是只能使用一次的,所以不能,不合法。因此,我们需要对原数组进行降重处理。
此外,如果原数组为{1,2,3,4,5,6,7}恰好为公差为1的等差数列,那么获取相等最多的数组就是将序列1~7反向添加,也就是{8,8,8,8,8,8,8}。那么我们去掉部分并延展这个原数列{1,4,7,12,13,14,15,16,20}
极端情况下思考,为了使相等的元素尽量多,我们会让原数组最小的值最大化,最大的值最小化,即最小的值加上序列的最大值,最大的值加上序列的最小值。如果满足a(min)+n>=a(max)+1,那么在原数组区间内(min~max),是不是有多少值,我们都有相对应的序列进行匹配,又因为我们进行了降重操作,所以无需考虑重复,因此,我们需要进行排序操作
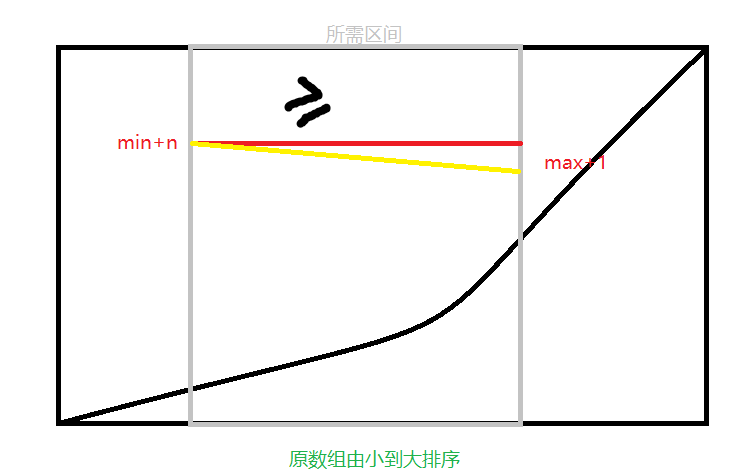
思路综上所述,以下是代码实现
include<bits/stdc++.h>
using namespace std;
int t, n;
vector
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
vector
for (int i = 0; i < n ; i++) {
scanf("%d ", &a[i]);
}
sort(a.begin(), a.end());
a.erase(unique(a.begin(), a.end()), a.end());
int m = a.size(), res = 0;
for (int l = 0, r = 0; r < m; r++) {
while (l <= r && a[r] + 1 - a[l] > n)l++;
if (l <= r && a[r] + 1 - a[l] <= n)res = max(res, r - l + 1);
}
printf("%d\n", res);
}
return 0;
}