机器学习-决策树算法详解

决策树算法

决策树算法是一种流行且功能强大的工具，用于机器学习、数据挖掘和统计学等各个领域。它们通过对不同变量之间的关系进行建模，提供了一种基于数据的决策的清晰直观的方法。本文将介绍什么是决策树、决策树的工作原理、决策树的优缺点以及决策树的应用。

什么是决策树？

决策树是一种流程图式结构，用于做出决策或预测。它由表示对属性的决策或测试的节点、表示这些决策结果的分支以及表示最终结果或预测的叶节点组成。每个内部节点对应于对属性的测试，每个分支对应于测试结果，每个叶节点对应于类标签或连续值。对于该算法的使用者来说，有2个难点需要关注：1，决策树的构建规律。2 ，决策树过拟合的解决方法——剪枝。

决策树的结构

1. 根节点：代表整个数据集和要做出的初步决定。
2. 内部节点：表示对属性的决策或测试。每个内部节点有一个或多个分支。
3. 分支：表示决策或测试的结果，通向另一个节点。
4. 叶节点：表示最终决策或预测。这些节点不再进行进一步的分裂。

举个例子，假设你试图评估一个人是否要买一辆汽车，你可以使用以下决策规则来做出选择：

数据集结构类似, (汽车颜，汽车年份，汽车品牌， 汽车行驶里程，购买结果)  。经过对数据集的训练后，获得的决策树模型如下：

 

 

 

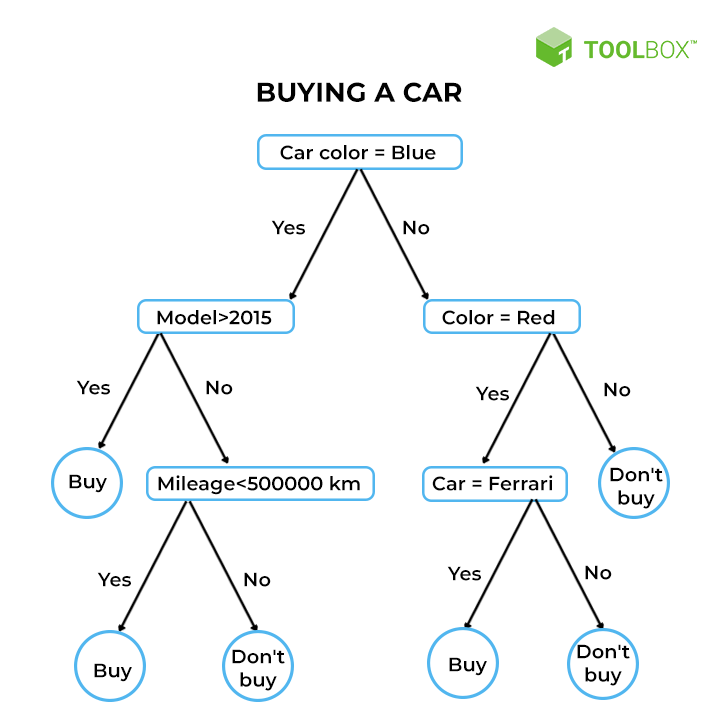
决策树如何工作/生成？

因为决策树是一个可迭代结构，所以当我们有了生成第一个节点的方法后，重复这一过程就可以。  第一个节点构建中，我们需要确定选取哪一个属性作为判断节点，

然后，确定2个判断后的分支结果 。

一个通常的构建决策树的过程包括：

1. 选择最佳属性：使用基尼不纯度、熵或信息增益等指标，选择分割数据的最佳属性。这是决策树算法的核心，它直接推动了决策树结构的生长。（具体过程见拆分指标）
2. 拆分数据集：根据所选属性将数据集拆分为子集。
3. 重复该过程：对每个子集递归重复该过程，创建一个新的内部节点或叶节点，直到满足停止标准（例如，节点中的所有实例都属于同一类或达到预定义的深度）。

拆分指标

基尼不纯度：衡量如果根据数据集中的类别分布对新实例进行随机分类，则该实例被错误分类的可能性。

熵 ：测量数据集中的不确定性或杂质的数量。这里我详细说说熵指标构建节点的过程。熵的取值范围为[0, 1] ,熵越大，说明数据集的信息量越大，最大为1. 所以当取数据集中某一个属性进行划分（注意：当前熵时，还没有划分，只是存在这样的一个划分。属性是自变量，而划分的分类　　　　　　       是因变量，也是预测的结果）时，它的信息熵计算公式如下：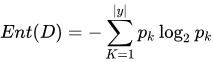

       ，其中，当前数据集  中有  类，其中第  类样本占比为 。 比如 购车数据集内，购车结果有2个分类，根据样本可以计算它的信息熵。这个也可认为是根节点的信息熵。

信息增益：衡量的是我们选择某个属性进行划分时信息熵的变化（可以理解为基于这个规则划分，不确定性降低的程度）。 比如继续引入 “汽车颜色”这个属性（划分）后对这个数据集熵的下降程度是多少。计算公式为：

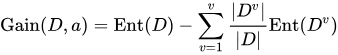 　　 ，其中 a是一个划分属性。 D^v 是该划分下的一个样本集合。最后，我们对所有的属性都进行一次划分，并计算信息增益，取使得增益最大的属性作为第一个节点。

决策树的优点

• 简单性和可解释性：决策树易于理解和解释。其视觉表现形式与人类的决策过程非常相似。
• 多功能性：可用于分类和回归任务。
• 无需特征缩放：决策树不需要对数据进行规范化或缩放。这样，前期的数据预处理方面大大简化。
• 处理非线性关系：能够捕捉特征和目标变量之间的非线性关系。

决策树的缺点

• 过度拟合：决策树很容易过度拟合训练数据，尤其是当决策树很深且有很多节点时。发生过度拟合后，该算法对于 测试集预测率高，但在实际预测中表现不好。
• 不稳定性：数据的细微变化可能会导致生成完全不同的树。
• 偏向具有更多级别的特征：具有更多级别的特征可以主导树结构。

修剪

为了克服过度拟合，可以使用修剪技术。修剪通过删除在分类实例方面提供较小能力的节点来减小树的大小。修剪主要有两种类型：

• 预修剪（早期停止）：一旦树满足某些标准（例如，最大深度、每片叶子的最小样本数），就停止树的生长。
• 后期修剪：从成年树上去除那些不能提供强大动力的树枝。

 

决策树的实例

这个实例是用于预测印第安皮马人的患糖尿病的判断模型，数据集结构为（怀孕次数，血浆葡萄糖浓度，血压，皮肤厚度，血清胰岛素浓度，BMI，糖尿病家系, 年龄，结果）

# 加载库
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split 
from sklearn import metrics # 加载数据集
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']pima = pd.read_csv("pima_indians_diabetes.csv", header=None, names=col_names)
pima.head()# 分离 特征变量和目标变量数据
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols]
y = pima.label#  切分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)# 创建决策树模型，并训练模型
clf = DecisionTreeClassifier(criterion="entropy", max_depth=3)
clf = clf.fit(X_train,y_train)# 预测测试集数据
y_pred = clf.predict(X_test)# 显示预测集数据准确度
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
# 后续还有模型优化