SMU Summer 2024 Contest Round 1
Dice and Coin
题意
给个 n 面骰子和一枚硬币,初始投骰子,若骰子的值在 1 到 \(K-1\) 之间则反复投硬币,硬币为正则该值翻倍,否则为 0 ,当值为 0 输掉游戏或者大于等于 \(K\) 时赢得游戏结束,问你可以赢得游戏的概率为多少。
思路
以 1 到 n 为初始值时,因为骰子为正时其值倍增,即一定是乘以一个 \(2^x\) 后大于等于 \(K\) ,所以以该值赢得游戏的概率就是 \(\frac{1}{x}\) ,累加 n 个初始值的胜利概率后除以 n 即可。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, k;cin >> n >> k;double ans = 0.0;i64 res = 1;vector<i64> c(50);for (int i = 0; i <= 30; i ++) {c[i] = res;res *= 2;}for (int i = 1; i <= n; i ++) {for (int j = 0; j <= 30; j ++) {if (c[j] * i >= k) {ans += 1.0 / (1.0 * c[j]);break;}}}ans /= n;printf("%.10lf\n", ans);return 0;
}
equeue
题意
给定一个长度为 n 的序列,和一个最大操作次数 k。
有以下四种操作:
- 操作 A:在序列左侧取走一个数放入手中。
- 操作 B:在序列右侧取走一个数放入手中。
- 操作 C:将手中任意一个数放在序列左侧。
- 操作 D:将手中任意一个数放在序列右侧。
也可以选择什么都不操作。
求在若干次操作后手中留下数的最大值。
思路
因数据量小,考虑暴力,但纯暴力会超时,因此需要使用优先队列优化。枚举操作A、B的次数,多出的次数则需要视情况执行C、D操作,若我们手中有一个负数,那么放回去可以使最终的和增大,反之我们则不操作,放回去的顺序一定是从小到大,负数越小,增大越多。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, k;cin >> n >> k;vector<int> a(n + 1);for (int i = 1; i <= n; i ++)cin >> a[i];i64 ans = 0;priority_queue<int, vector<int>, greater<int>> Q;for (int i = 0; i <= k; i ++) {for (int j = 0; j + i <= k && j + i <= n; j ++) {for (int l = 1; l <= i; l ++)Q.push(a[l]);for (int r = n; r > n - j; r --)Q.push(a[r]);i64 res = k - i - j;while (Q.size() && res-- && Q.top() < 0) Q.pop();res = 0;while (Q.size()) {res += Q.top();Q.pop();}ans = max(ans, res);}}cout << ans << '\n';return 0;
}
Sequence Decomposing
题意
给 n 个数,满足 $i < j $ 并且 \(A_i < A_j\)条件的可以染成一个颜色,问最少需要多少颜色可以全染色。
思路
其实类似就是让你找出若干个递增子序列,答案就是递增子序列的数量,因此我们可以从后往前枚举当前值,将当前值放在已有的递增子序列里末尾最接近它的那个序列里,比如当前值为 5 ,现有两个递增子序列 6 7 … 和 7 8 … ,最优应该是放在 6 后面,7 留给更有可能性的,否则之后再碰到 6 就需要重新以它为终点再开一个序列,那样就不是最少了。
这里我是用一个数组只存了每个序列的末尾一个数,因为也只用到这个数,当序列里有满足要求的就放进去,替换掉最后一个,否则新建一个序列。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;vector<int> a(n + 1);for (int i = 1; i <= n; i ++)cin >> a[i];int sum = 0;vector<int> c;for (int i = n; i > 0; i --) {auto t = upper_bound(c.begin(), c.end(), a[i]);if (t == c.end()) {c.push_back(a[i]);} else {*t = a[i];}}cout << c.size() << '\n';return 0;
}
Cell Distance
题意
给一个 \(n\times m\) 的矩阵,从中选出 \(k\) 个点,用 \(∑_{i=1}^{K−1}∑_{j=i+1}^K(∣x_i−x_j∣+∣y_i−y_j∣)\) 计算其贡献,问你将所有方案的贡献总和模 1e9+7 的答案。
思路
转换一下,先考虑 x 坐标的贡献(将 y 的贡献看成 0 )。
考虑两个点间 x 坐标相差为 \(d(1 ≤ d ≤ n−1)\) 时的贡献(\(d=0\) 的时候没有贡献所以这里不考虑)。设这两个点的坐标为 \((x_1,y_1)、(x_2,y_2)\),那么就有 \(x_1 − x_2 = d,1 ≤ x_1 ,x_2 ≤ n,1 ≤ y_1 ,y_2 ≤ m\)。
则可行的 \(x_1,x_2\) 有 \(n−d\) 对 \(\{(x_1,x_2)|(1,𝑑+1),(2,𝑑+2),⋯ ,(𝑛−𝑑,𝑛)(1,d+1),(2,d+2),⋯,(n−d,n)\}\),\(y_1,y_2\) 各有 m 种取法。所以像这样的点对共有 \((n-d) \times m^2\) 对,每一对的贡献为 d,总的贡献就是 \(d \times (n - d) \times m^2\)。
每一个点对出现在选出的 k 个点中的方案数共有 \(𝐶_{𝑛×𝑚−2}^{𝑘−2}\) (除去这两个点之外,剩下 n×m−2 个点中,选出 k−2 个点,与这两个点组成要选出的 k 个点),那么总的贡献就是 \(d×(n−d)×m^2×C_{n×m−2}^{k−2}\)。
同理可以计算 y 坐标的贡献,得到最终答案为:
\((\sum_{d=1}^{n-1}d\times (n-d)\times m^2 +\sum_{d=1}^{m-1}d\times (m-d)\times n^2)\times C_{n \times m - 2}^{k-2}\)
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;const i64 mod = 1e9 + 7;i64 ksm(i64 x, int y) {i64 res = 1;while (y) {if (y & 1) res = res * x % mod;x = x * x % mod;y >>= 1;}return res;
}i64 C(int n, int m) {i64 res = 1;for (int i = 1; i <= m; i ++)res = res * (n - m + i) % mod * ksm(i, mod - 2) % mod;return res;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m, k;cin >> n >> m >> k;i64 ans = 0;for (int d = 1; d < n; d ++)ans = (ans + 1ll * d * (n - d) % mod * m % mod * m) % mod;for (int d = 1; d < m; d ++)ans = (ans + 1ll * d * (m - d) % mod * n % mod * n) % mod;ans = ans * C(n * m - 2, k - 2) % mod;cout << ans << '\n';return 0;
}
Friendships
题意
给你 n 个点,要你构造出 k 对距离为 2 的无向连通图,不能有自环和重边,如无法构造则输出 -1。
思路
距离为 2 的两个点中间必然会经过一个点,所以当拿出一个点作为所有距离为 2 的点对的中间点时,此时这个图的距离为 2 的点对达到最大值,也就是常说的菊花图。
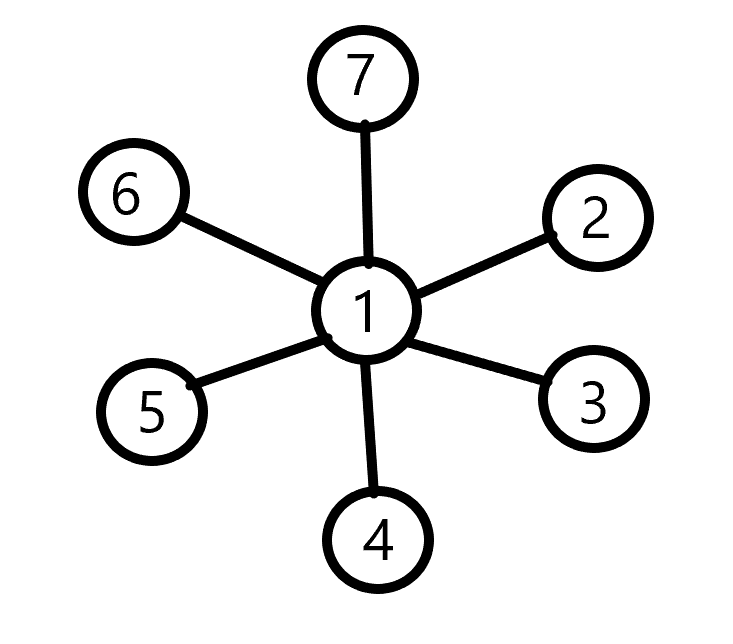
通过菊花图可以得到最多 \(m = \frac{(n-1)\times(n-2)}{2}\) 个距离为 2 的对数,这也是一个无向连通图能得到最大距离为 2 的点数,因此当 k 大于这个值时,说明不可能构造出来,小于这个值的时候我们只需要添加 \(k-m\) 条边使得这些点连成环即可。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, k;cin >> n >> k;int all = (n - 1) * (n - 2) / 2;if (k > all) {cout << "-1\n";} else {cout << n - 1 + all - k << '\n';for (int i = 2; i <= n; i ++)cout << i << " 1\n";for (int i = 2; i <= n; i ++)for (int j = i + 1; j <= n; j ++) {if (all == k) return 0;cout << i << ' ' << j << '\n';all --;}}return 0;
}
Integer Cards
题意
给 n 个数和 m 次操作,每次操作给出 B、C 两个数,可以将数组中不大于 B (可以为 0 )个数修改成 C 的值,问最后这个 n 个数的和最大为多少。
思路
考虑离线做法,先将这 m 次操作处理出来,然后排序,这里因为map里自动排序了所以直接存进 bc 数组了,然后就是从 c 值大的往小的枚举,每次直接用一个multiset 处理可以被替换掉的数字即可,因为是从大到小的处理,所以复杂度不会有 \(O(n^2)\)。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;multiset<int> s;vector<i64> a(n + 1);for (int i = 1; i <= n; i ++) {cin >> a[i];s.insert(a[i]);}vector<array<int, 2>> bc;map<int, int> mp;for (int i = 0; i < m; i ++) {int b, c;cin >> b >> c;mp[c] += b;}for (auto &[c, b] : mp) {bc.push_back({c, b});}for (int i = bc.size() - 1; i >= 0; i --) {auto [c, b] = bc[i];while (c > *s.begin() && b) {b --;s.erase(s.begin());s.insert(c);}}i64 ans = 0;for (auto i : s)ans += i;cout << ans << '\n';return 0;
}